Keywords

Solvency II, Solvency Capital Requirement, Actuarial Calculations.

Introduction

Since 2016, the European insurance and reinsurance practice has applied Directive 2009/138/EC "Directive of the European Parliament and of the Council on the taking-up and pursuit of the business of Insurance and reinsurance (Solvency II)" (Directive, 2009), which introduces new regulatory requirements to guarantee the solvency of insurance and reinsurance companies. The application of the directive is based on the European Commission (EU) Regulations 2015/35 from 10.10.2014 "Supplementing Directive 2009/138/EC of the European Parliament and of the Council on the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II)" (Regulation, 2014).

Prior to this, there were applied the "Solvency I Life Directive" 2002/12/EC and "Solvency I Non-life Directive", 2002/13/EC, which set the minimum Solvency Capital Requirement on the basis of insurance premiums and payments. The mechanism close to Solvency I is applied in Russia (E.A., 2013): The required size of the equity capital of general insurance should be not less than the highest of the two numbers- 16 per cent of the annual bonus or 23 per cent of the annual average loss for the last three years and of life assurance- at least 5 per cent of the life assurance reserve. In all circumstances, the equity capital must be not less than the minimum amount established by the Insurance Supervision Body.

This approach did not have a strict scientific basis and did not take into account many significant characteristics of the particular insurance portfolio that affect the distribution of the expected value of future insurance payments.

Directive Solvency II establishes a risk management system within an insurance or reinsurance company. There are three ways to secure the reliability of insurance financial institutions:

1. Quantitative requirements for capital;

2. Management and supervision of insurance and reinsurance organizations;

3. Information disclosure and transparency.

The first direction defines the minimum necessary value of own capital- Solvency Capital Requirement, SCR. The probabilistic model is used for the SCR definition: The equity capital must be sufficient to cover possible payments and expenses with a probability of not less than 0.995 during the year.

The need for equity capital is determined either by the so-called standard formula (Solvency II Standard Formula) or by an internal probabilistic risk modeling of the internal model (internal models) developed and consistently applied by the insurer. In the case of using of an internal model, the insurer must prove to the oversight body the adequacy of the model, its understanding of the company's highest management and the actual use of the key management decisions (use test).

The standard formula is a combination of SCR particular values for individual risk modules: Underwriting risk of life insurance, general insurance (non-life insurance) and health insurance and non-insurance risks: Market, credit and operational. For each module, the SCR value must be established so that it goes around covering the related costs likely to 0.995.

In fact, the introduction of Solvency II is a transition to an economically viable model of insurance supervisory, which is first to be based on risk assessment and management. In particular, the determination of the Solvency Capital Requirement (SCR) was carried out for the first time through value-at-risk with a specified level of reliability-0.995.

Problem Statement

However, despite considerable progress, a number of issues remain unresolved in the application of the standard formula Solvency II.

For example, the SCR value of the underwriting risk of general insurance is a combination of three subunits: Premium and reserve risk sub-module, catastrophe risk sub-module and risk of early termination of insurance and reinsurance contracts (lapse risk sub-module) (Directive, 2009).

The SCR value of the premium and reserve risk sub-module is calculated as value of standard deviation of the risk amount multiplied by the 3, which is determined on the basis of:

1. Amounts accrued or received net-premiums for the preceding 12 months;

2. Expected net-premiums for the future 12 months;

3. The most appropriate assessment of loss reserves;

4. Desired value of standard deviation of premiums and reserves amount for insurance business segments;

5. The prescribed values of correlation parameters between the different segments of the insurance business.

Multiplier 3 is intended to achieve a specified level of reliability: Under the "three sigma" rule, the probability of finding a normally distributed random measure within three standard deviations is 0.9973.

According to the calculation method, with the reduction of the insurance premium, the SCR value is reduced by the premium and reserve risk sub-module. However, if the insurance company has set a lower premium than is required, the Solvency Capital Requirement (SCR), in reverse, should increase to maintain a specified level of reliability not less than 0.995. Consequently, the standard model does not compensate the supervening of insurance premiums understatement. The opposite is also true: If the insurance company charges an overvalued premium, the risk of premiums and reserves for it will be reduced, but the standard formula dictates to increase the value of its own capital.

The values of standard deviations of bonus and reserve amounts, as well as correlation parameters, are defined by expertise based on the results of statistical analysis. It is shown that established the standard formula Solvency II is not sensitive to the individual characteristics of the portfolio of a particular insurance or reinsurance company. By changing the quality of insurance contracts within the same insurance business segment, the insurance or reinsurance company may not affect the SCR value.

The use of disproportionate reinsurance is taken into account by empirically defined correction factors that are equal to 0.8 or 1, depending on the segment.

Thus, in the general insurance, the standard formula does not take into account the distribution of the expected collective loss in future, but is based only on the rates of premiums and reserves. In essence, the SCR definition of underwriting risk does not take into account the individual characteristics of the insurance portfolio. As a result, the complexity of the computation is significantly increasing, but an explanatory and predictive force of the model compared with Solvency I do not improve.

So do SCR in other insurance industries: Life insurance and health insurance. Thus, within the Solvency II, there is a problem of improving the adequacy of the SCR underwriting risk assessment. Based on the Directive 2009/138/EC recently entered into force, this problem must be solved without a radical change in Solvency II.

Model Using a Generalized Actuarial Basis

As mentioned above, the insurer completely may use the internal model instead of a standard formula if it is more accurately account the characteristics of the insurance portfolio and provides a more adequate assessment of the SCR underwriting risk (Directive, 2009). The internal model can be partial (partial internal model) when one or more modules or subunits have been replaced in the standard model. The internal model should correspond to the principles of Solvency II.

As an option for the internal model of underwriting risk, the equity capital model can be considered within the concept of a generalized actuarial basis. This model is presented as follows:

According to the concept of a generalized actuarial basis ( Ryzhkov, 2016), a single model for calculating insurance premiums, insurance reserves and Solvency Capital Requirement, based on a single set of baseline data (actuarial basis), can be applied for all the insurance industries and segments.

To date, the actuarial models of life insurance, health insurance and general insurance considerably differ in the calculation formula and the composition of the original data (the actuarial basis). Moreover, the separate development of models over time only increases the gap between the descriptions of mentioned insurance industries.

Doubts about the objective need for such differences led to suppose that there was a single actuarial basis and a single mathematical model of calculations. In this case, the general insurance contract, life insurance contract and the health insurance contract should be considered as private cases of a certain generalized insurance contract.

For all, without exception, actuarial calculations there is used data contained exclusively in the single source, it is the actuarial basis of the insurance risk. No additional information is used in the calculations. This requirement allows reaching the completeness and consistency of the source data, the transparency of the calculations and significantly enhances monitoring of the validity of the actuarial calculations.

The actuarial basis includes estimates of the insurance risk data such as: The intensity of the occurrence of insurance cases per policy through a unit of time; the law of distribution of insurance payments in tabular form; the intensity of early termination of insurance contracts; duration of the expectant period; deferrals and disbursements of premiums and insurance premiums; delays in insurance payments; fixed and variable business expenses; distribution law of insurance amount and its changes over time in tabular form; the distribution functions in the course of the risk division and the rate of return (discounting); the level of reliability of the insurance premiums and the estimated level of the insurance portfolio (Ryzhkov, 2011). The pointed parameters of the actuarial basis are determined by statistical observation and if the parameter is not a random variety or observation data is not sufficient, than determined on the basis of non-statistical information, special calculations or expert estimation. All the parameters of the actuarial basis should be confirmed by the documents and are the subject of oversight bodies monitoring.

Modeling of a sufficient number of insurance portfolios is carried out on the basis of the actuarial basis of the Monte-Carlo method. For each time t and the insurance contract, the amount of future expenses that will be incurred under this contract after time t is determined. The amount is discounted to the time the insurance contract is concluded and ordered in ascending order to produce. The result is a number of discounted forthcoming expenses 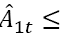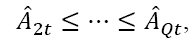where Q is the number of insurance contracts, the signˆ indicates discounting.

Using this series, it is easy to calculate the amount of the upcoming payments after a time that is not exceeded with the probability (reliability level of insurance premiums):

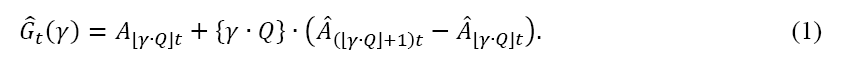
Here, parentheses⌊⌋ represent the whole part of the number and the parentheses{} are the fractional part of the number.

The value ˆG₀ corresponds to the insurance premium that is paid at the time of the conclusion of the insurance contract, the amount G_t, t > 0of time t, i.e., without discounting, the total amount of the insurance reserves at the time t. Insurance premiums (tariffs) (Bobrov, & Ryzhkov, 2013) may be calculated, including the risk dividing (Bobrov, 2012) as well as insurance reserves ( Ryzhkov, 2015b; Bobrov & Ryzhkov, 2015).

The application of this technique allows calculating the insurance premiums and insurance reserves, without assumptions about the specific analytical form of the loss distributive law, take into account in calculations the variation of virtually any parameters, the existence of delays, postponements, early termination and the application of franchises, reinsurance and other methods of dividing the risk.

In determining of one or another actuarial basis parameter, its different estimates may be obtained, which can be used in the calculations with equal justification. The multiplicity of estimates of the parameters of the actuarial basis gives rise to uncertainty about the results of insurance premiums and insurance reserves. The actuarial basis documents a number of alternative values of the parameter in ascending order. In this case, preliminary the parameter value is specified by Monte-Carlo method (Ryzhkov, 2015a), while modelling a contract. This method is based on the same principle as the bootstrap method (Efron, 1993).

Resulting number of discounted future costs will also take into account the uncertainty of the source data.

By virtue of a formula (1), any real size of the premium P can always be matched by its actual level of reliability of insurance premiums 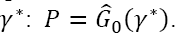Therefore, in a case where the value of the insurance premium (or insurance tariff) is different from that of the formula (1) for the level of reliability and the moment of time t=0, it is possible to find a measure γ^*based on a number 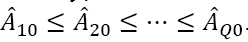In the particular case, when the actual value of the insurance premium corresponds to the one gotten with formula (1), equality has been fulfilled: γ^* = γ.

If the earmarked funds are not sufficient, the costs are covered by the insurer's own capital. Consequently, the required value of equity capital is determined on the basis of the amount of insurance payments that cannot be covered by the insurance reserves.

As indicated earlier, the level of reliability of Solvency II is γ^'. Therefore, the need for equity capital at the appropriate insurance risk at the time t will be:

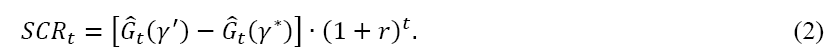
Here, r is the discount rate per unit of time provided by the actuarial basis and 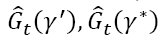is determined by formula (1).

Discussion of Results

From a meaningful point of view, the value (2) is the sum of the funds that the insurer is further required exceeding the amount of the insurance reserves to ensure that the reliability level is not lower than γ^'( Ryzhkov, 2014).

It is straightforward to see; the proposed model meets all the principles of Solvency II and is universal for all insurance risks. The results of the calculations are based solely on the confirmed data of generalized actuarial basis, which ensures a complete enumeration of all factors that are significant for the actuarial calculations. The SCR value by formula (2) will take into account the individual features of the particular insurance portfolio. The estimate of its own capital is understandable and consistent with the level of insurance reserves and insurance premiums, based solely on the baseline data used in the calculation of insurance premiums and reserves.

These advantages allow the proposed model to be considered as a possible variant of the internal model at the underwriting risk.

In order to verify the applicability of the generalized actuarial basis, special software was developed and a number of computational experiments on the calculation of insurance premiums, insurance reserves and the necessary value of their own capital (for example, Bobrov & Ryzhkov, 2014) was carried out. The results confirmed the universality of the calculation models based on the generalized actuarial basis and their practical applicability.

Unlike the standard Solvency II formula, the proposed model only takes into account the obligations under existing insurance contracts and does not consider the contracts to be concluded in the future. The determination of the required value of equity capital, taking into account future obligations, is possible by calculation of the formula (2), both for the current time t and for the moment in 12 months, in the assumption that all the planned contracts are concluded and the choice of the larger of the two values:

Here n is the number of time periods corresponding to 12 months because, actually, for the purposes of applying equations (1)-(3) time can be measured in any unit.

It is clear that, in effect (2), the required value of equity capital at any time is not so much related to actual bonuses and payments, but to the amount of insurance reserves ˆG_t. As shown in (Ryzhkov, 2008), there is a constant 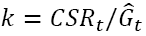that uniquely identifies the required value of its own capital through the amount of insurance reserves on the reporting date: 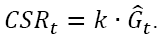The k value can be set during the development phase of insurance tariffs. Such a model could significantly simplify the calculations within the Solvency II. However, it has increased requirements for the reliability of the assessment of premiums and insurance reserves.

References

1. Bobrov L.K. & Ryzhkov O.Y. (2012). Calculation of the insurance rate on the basis of a generalized actuarial basis with risk taking into account. Bulletin of NSUEM (1), 188-196.
2. Directive. (2009). Directive 2009/138/EC of the European Parliament and of the Council. On the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II), recast. EUR-Lex–32009L0138.
3. E.A., Y. (2013). Internal model of the insurance company within Solvency II (use test). Scientific Researches of The Economic Faculty, 5(10), 77-89.
4. Efron B., T.R.J. (1993). An introduction to the bootstrap. New York: Chapman & Hall.
5. O.Yu., R. (2008). Financial stability of insurers: Evaluation and management (PhD thesis). Novosibirsk.
6. O.Yu., R. (2011). Generalized actuarial basis of insurance risk. Bulletin of NSUEM(2), 166-178.
7. O.Yu., R. (2014). What amount of equity is needed to the insurance company? Ideas and Ideals, 2(3), 106-113.
8. O.Yu., R. (2015a). Elimination of uncertainty of initial data in actuarial calculations. Proceedings of the II International Scientific and Practical Conference “Management Technologies and Models of Modernization Processes in the Russian Economy: History and Modernity”. Kursk, 100-106.
9. O.Yu., R. (2015b). The method of formation of insurance reserves using the generalized actuarial basis. Bulletin of NSUEU(1), 114-136.
10. O.Yu., R. (2016). Actuarial calculations in insurance on the basis of a generalized actuarial basis with the use of statistical modelling. Questions of Statistics (1), 54-62.
11. Regulation, C.D. (2014). Commission Delegated Regulation (EU) 2015/35 of 10 October 2014 supplementing Directive 2009/138/EC of the European Parliament and of the Council on the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II). EUR-Lex - 32015R0035–EN.
12. Ryzhkov O.Yu. & B.L.K. (2013). Tariffication of the insurance contract on the basis of a generalized actuarial basis. Bulletin of the Saratov State Technical University, 4(1), 329-336.
13. Ryzhkov O.Yu. & B.L.K. (2014). Estimation of the accuracy of the numerical method for calculating insurance tariffs, based on the generalized actuarial basis. Bulletin of NSUEM, 4, 60-80.
14. Ryzhkov O.Yu. & B.L.K. (2015). Formation of insurance reserves using a generalized actuarial basis. Bulletin of the Astrakhan State Technical University. Series: Management, Computer Science and Informatics (3), 85-95.
15. Ryzhkov O.Yu. & L.M.V. (2007). Financial stability of insurance organizations: Assessment and management. Institute of Economics and Industrial Organization. Novosibirsk.