Keywords

SFAS 133, SFAS 161, Derivatives, Bank Holding Companies, Notional Amounts.

JEL Descriptors

M40, M41, M49, G10, G12, G13, G20, G21.

Data Availability

The data used in this study is available from public sources indicated in the paper.

Introduction

The use of a growing array of derivatives and the related application of more-sophisticated approaches to measuring and managing risk are key factors underpinning the greater resilience of our largest financial institutions. Derivatives have permitted the unbundling of financial risks.

I view derivatives as time bombs, both for the parties that deal in them and the economic system. Financial weapons of mass destruction, carrying dangers that, while now latent, are potentially lethal.

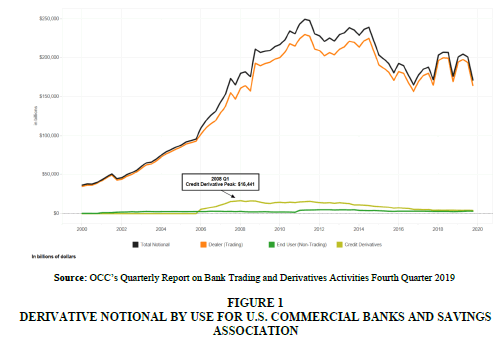
The views on the use of derivatives expressed by the former Chair of the Federal Reserve Board, Alan Greenspan, and billionaire investor Warren Buffet give us a glimpse of the contrasting views and perceptions individuals have on derivatives. According to the quarterly reports issued by the Office of the Comptroller of the Currency, in mid-2007, when signs of the crisis started showing up, the top 25 U.S. Bank Holding Companies (BHC) held over $160 trillion dollars in derivatives based on notional amounts. By the end of 2019, despite the role derivatives played in exacerbating the crisis, these banks held over $228 trillion dollars in derivative notional amounts. This represents an increase of 43% despite the negative press they received. Figure 1 below illustrates the increasing use of derivatives throughout the last 20 years for Commercial Banks.

Despite all the negative publicity received by derivatives, their continued and incrementing use serves as confirmation of their value to our financial markets. Derivatives, when used properly, help firms manage risk for which they otherwise would have no other medium. While negative instances of the use of derivatives make headline news, positive and responsible use of derivatives goes unnoticed on a daily basis. Because of their relatively higher exposure to financial risks, such as interest rate and foreign exchange risk, banks have a greater need to manage such risks. These banks find that derivatives, when used properly, are an effective and cost-efficient way to manage such risks. Indeed, the use of derivatives as a responsible risk management tool and their ability to permit the transfer of risk led Alan Greenspan to extoll their virtues.

The accounting and disclosure of derivatives has evolved throughout the years. The FASB continues to attempt to improve the transparency of such disclosures. The most recent statements, SFAS 133 and SFAS 161, have further improved the disclosures of such derivatives. One of the main changes made by SFAS 133 to improve the transparency of information was the requirement that the fair values of derivatives be recognized on the face of the financial statements. SFAS 161 re-introduced the requirement that notional amounts be disclosed and that such information be presented in a vastly more organized and easily readable tabular format.

This study, making use of such tabular data, examines if markets indeed value these specific classifications differently and if so, how do they relate to firm valuation. In particular, the research design focuses on the notional values of such derivatives and specifically distinguish between the hedging and non-hedging categories. Because most banks implemented SFAS 161 starting in 2009 the sample period covered in this study will be from 2009 up to December 2019 using quarterly data.

This paper finds that notional amounts of hedging derivatives are negatively correlated to firm valuation. This implies that while these derivatives may be effectively reducing the risk of the firm, they do it at a cost expressed in the form of return. The study finds that before controlling for trading revenues, notional amounts of non-hedging derivatives are positively related to firm valuation. Once we control for trading revenue, the relationship turns negative suggesting that any positive association between non-hedging derivatives and firm valuation is strictly related to their revenue generating potential. In fact, the negative coefficient for non-hedging derivatives is larger and significantly different than that for hedging derivatives.

This study contributes to prior research in that it is one of the few, if not the only one, to take the information directly from the new and improved SFAS 161 disclosure tables. Furthermore, it incorporates and examines a major driver of results which is rarely mentioned in prior research, related trading revenues.

The remainder of this paper is organized in the following manner. Section II describes the evolution of derivative accounting standards and related research. Section III provides a review of the theories that motivate my hypotheses. In Section IV presents information on the sample data and their descriptive statistics. Section V pertains to the empirical analysis and results obtained. Section VI concludes the paper with some final thoughts.

Derivative Accounting and Related Research

Derivative Accounting under SFAS 105, SFAS 107and SFAS 119

The first standards addressing derivative accounting and disclosures were SFAS 52 (1981) and SFAS 80 (1984). These standards were considered suboptimal in addressing the complex issues related to derivatives; they were difficult to apply consistently across all types of derivatives and failed to provide the transparency statement users desired (Duangploy & Helmi, 2002). In May of 1986, the FASB began a long-term project with the objective of issuing new standards that would improve on the existing ones. SFAS No. 105 was the first new statement borne out of this project. SFAS No. 105, Disclosure of Information about Financial Instruments with Off-Balance- Sheet Risk and Financial Instruments with Concentrations of Credit Risk, became effective for financial statements issued for fiscal years ending after June 15, 1990. One of its main features was the requirement that all financial instruments that carry off-balance sheet risk of accounting loss be disclosed. Off-balance sheet risk refers to the potential loss attributable to a financial instrument which is not currently recognized in the balance sheet. The statement extended prior disclosure practices by requiring new disclosures relating to financial instruments with potential off-balance sheet risk of accounting losses. SFAS No. 105 is often cited by researchers in supporting the use of notional amounts as a construct for the derivatives comprehensive risk exposure. In particular, researchers point out paragraph 89 which states the following:

The Board concluded that disclosing information about the face or contract amount (or notional principal amount) of financial instruments with off-balance-sheet risk provides a useful basis for assessing the extent to which an entity has open or outstanding contracts. The disclosure of that amount is intended to apprise investors, creditors, and other users that the entity is engaged in certain activities whose off-balance-sheet risk is beyond what is currently recognized in the statement of financial position. The face or contract amount gives investors and creditors an idea of the extent of involvement in transactions that have off-balance-sheet risk. That information conveys some of the same information provided by amounts recognized for on-balance-sheet instruments.

SFAS No. 107, Disclosures about Fair Value of Financial Instruments, was issued in December of 1991 and became effective after December 15, 1992 for firms with $150 million or more in total assets. SFAS No. 107 broadened the fair value disclosures under SFAS No. 80, which only covered exchange traded futures contracts, to include all financial instruments including derivatives.

SFAS No. 107 lacked clarity as it did not require separate disclosure of the fair values of derivative instruments and other financial instruments. In response to the lack of clarity, the FASB issued SFAS No. 119 in October of 1994 to be effective after December 15, 1994. SFAS No. 119 required the disclosures of fair values for derivative instruments be presented separately from that of other financial instruments. A recurring criticism of prior standards was that it was very difficult to ascertain if the fair values disclosed were assets or liabilities (Venkatachalam, 1996). This standard attempted to rectify this ambiguity by requiring a clearer distinction of fair value positions than previous standards. It also required the distinction between derivatives used for trading purposes from those not used for trading purposes.

Derivative Accounting under SFAS 133and SFAS 161

SFAS No. 133, Accounting for Derivative Instruments and Hedging Activities, was issued on June of 1998 to be effective after June 15, 1999. The effective date was later deferred to June 15, 2000 by SFAS No. 137. The most significant change brought on by this statement was the requirement that fair values of derivatives be recognized on the face on the statement of financial position. This requirement was opposed by many in the banking industry; arguing that it would substantially increase the volatility of the industry’s financial statements. Ironically, they also claimed that the information was already being provided under SFAS 107 and SFAS 119 (Duanploy & Helmi, 2002). To this day, it is considered the most complex accounting standard ever passed. If meeting certain specific conditions, a derivative would be classified as one of three types of hedging derivatives and the accounting of changes in fair values (gains and losses) would depend on its classification. The three categories of hedging derivatives created were: a) a fair value hedge is a hedge to the exposure of changes in fair value of a recognized asset, liability, or unrecognized firm commitment. Gains or losses are postponed and recognized in the same period in which the hedged items gains or losses are recognized so as to offset each other. Any gain or loss attributable to hedge ineffectiveness is recognized immediately, b) a cash flow hedge is a hedge to the exposure of a forecasted transaction. The gains and losses on the effective portion of the hedge is recorded in comprehensive income until the forecasted transaction takes place when it is reclassified into earnings, c) a hedge of foreign currency exposure of a net investment in a foreign operation, unrecognized firm commitment, available for sale security (AFS), or foreign currency denominated forecasted transaction. Gains and losses for net investments are recorded in other comprehensive income under cumulative translation adjustment. Gains and losses for the currency exposure of unrecognized firm commitments and AFS securities are treated similar to fair value hedges and forecasted transaction currency exposure gains and losses are treated similar to cash flow hedges. For derivatives not classified as hedging instruments, gains and losses are recognized immediately. The method used to assess hedge effectiveness must be established before the derivative is classified as a hedging derivative. In summary, SFAS 133 either amends or supersedes all previously aforementioned statements relating to derivatives (Barth, 1991).

SFAS No. 161, Disclosures about Derivative Instruments and Hedging Activities—an amendment of FASB Statement No. 133, was issued in March of 2008 and became effective for financial statements issued after November 15, 2008. The most recent statement considerably improves the amount and transparency of disclosures required for derivatives. This statement helps overcome the intentional obfuscation of derivative disclosures management had previously carried out. It requires information pertaining to fair values, risk type, gains and losses, accounting designation, and location on the statement to be presented in an easy to read tabular format. Another significant amendment introduced by this statement was the requirement that derivative notional amounts be disclosed; a requirement which had been discontinued in SFAS No. 133.

Table 1 shows a sample of one of the new and improved disclosure tables.

Table 1 Shows A Sample Of One Of The New And Improved Disclosure Tables
SunTrust Banks, Inc.
Notes to the Consolidated Financial Statements (Unaudited), continued As of December 31, 2012 Asset Derivatives
	Balance Sheet	Notional	Fair	Notional	Fair
(Dollars in millions)	Classifications	Amounts	Value	Amounts	Value
Derivatives designated in cash flow hedging relationships
Interest rate contracts hedging
Floating rate loans	Trading	$17,350	$771	$--	$--
Total		17,350	771	--	--
Derivatives designated in fair value hedging relationship
Interest rate contracts covering
Fixed rate debt	Trading	1.000	61	--	--
Total		1,000	61	--	--
Derivatives not designated as hedging instruments
Interest rate contracts covering:
Fixed rate debt	Trading	--	--	60	10
MSRs	Other	6,185	150	12,643	33
LIFS, IRLCs	Other	2,333	6	7,076	15
Trading activity	Trading	81,930	6,044	86,037	5,777
Foreign exchange rate contracts covering:
Commercial loans	Trading	--	--	34	--
Trading activity	Trading	2,451	66	2,326	63
Credit contracts covering:
Loans	Trading/Other	--	--	445	8
Trading activity	Trading	1,958	55	2,081	49
Equity contracts - Trading activity	Trading	15,748	1,342	22,184	1,529
Other contracts:
IRLCs and other	Trading/Other	6,783	132	142	1
Commodities	Trading	255	29	255	29
Total		117,643	7,824	133,283	7,514
Total derivatives		$135,993	$8,656	$133,283	$7,514

Among the most notable publications relating to these standards we find Ahmed et al. (2006). This study compares the value relevance of the post SFAS 133 recognized fair values to the pre SFAS 133 disclosed fair values. It finds that, while recognized fair values were value relevant, the disclosed fair values were not. A study done by Wang et al., (2002) finds mixed results as to the value relevance of the notional amounts under SFAS 133. This study only used two years of data; a possible reason for the limited findings. Other issues related to SFAS 133 have been researched. Finnerty & Dwight (2002) examine the methodological choice firms make to test for hedge effectiveness. Eckstein et al., (2008) examines the magnitude of cumulative effects of changes in accounting principle from the income statement in the year of adoption, market reaction to earnings announcements, and key financial ratios effects. In summary, research on the value relevance of notional values and their corresponding fair values under SFAS has not been too extensive and those that have studied the subject have had mixed results.

Motivation and Hypotheses Development

Very few studies, if any, have used post SFAS 161 data exclusively to test the value relevance of notional amounts of derivatives. Of the most notable studies, Riffe (1996) used SFAS 107 disclosures, Venkatachalam (1996) used SFAS 119 disclosures, Seow & Tam (2002) used SFAS 119 disclosures, and Wang et al., (2002) use a combination of SFAS 119 and 133 disclosures with the majority of the sample data provided under SFAS 119. The exclusive use of SFAS 133 data, enhanced with the SFAS 161 requirements, could provide updated information on the value relevance of such disclosures. SFAS 133 explicitly states the requirements for a derivative to qualify as a hedging instrument, perhaps increasing the perception of the risk reduction benefits of these particular derivatives and the reliability of the distinction as well. While prior studies have examined the distinct value relevance of risk management and trading derivatives, they fail to control for the revenue generating power of trading derivatives, a major distinction between both types of derivatives. Without such controls, any significant positive relationship between trading derivative notional values and stock returns may be picking up their revenue generating potential. It would be interesting to see how markets view these notional amounts once their related revenues are controlled for. This study uses post SFAS 133/161 data and controls for the trading revenue generated by derivatives.

Hypotheses Development

A basic model for the valuation of any asset is to discount all foreseeable future cash flows by a discount rate related to the risk associated with the actual occurrence of these cash flows. This risk, in turn, is associated with the systematic risk borne by such assets. Systematic risk is the risk that cannot be diversified away because it is associated with general market risks and unrelated to specific firm risks. Unsystematic risks are associated specifically with each asset and are also called idiosyncratic risks. Markets do not compensate for unsystematic risks because they can be diversified away. Derivatives are innovative financial instruments that can be used to reduce risk. It can be argued that derivatives are innovative financial instruments that can now help firms reduce their exposure to systematic risks or perhaps increase such exposure. Exposure to forces considered uncontrollable in the past such as international economic events, interest rates, or even acts of nature can be hedged against through the use of derivatives. But this reduction in exposure also comes at a cost. The act of hedging, while reducing the overall risk exposure of a firm, also limits its cash flows. At the extreme, a firm that hedges all of its cash flows under perfect hedges will act more like a risk-free investment. In other words, the act of hedging may shift the firm downwards in the risk/return spectrum. This shift is dependent on how the act of hedging affects the two main components of firm valuation, cash flows and discount rates. Venkatachalam (1996) finds results that are inconsistent with (Riffe, 1996). He finds that the coefficient on notional values of hedging derivatives is negative and significant. He attributes such results to the credit risk in derivative contracts. This can be interpreted as saying that while hedging instruments may reduce some forms of risk; this reduction is offset at least partially by the credit risk inherent on such derivatives therefore producing negative coefficients. In other words, the cash flow limitations imposed by such hedging strategies are not sufficiently offset by a risk reduction so as to produce a positive relationship with firm valuation. Skinner (1996) contends that such explanation does not necessarily rule out other explanations. He poses other potential explanation such as markets viewing hedging as an overly costly value reducing activity or that market participants don’t trust managers to use derivatives to reduce risk. Note how both of these alternative explanations are related to either cash flows or risk reduction. Wang et al. (2005) find some evidence of positive and significant coefficients for notional amounts of derivatives but fail to theorize why their results are so different from (Venkatachalam, 1996). Therefore, no prediction is made for the sign of derivative instruments used for hedging purposes and the following hypotheses are posited:

H₁: The notional amounts of hedging derivatives will be positively related to firm valuation when markets perceive their risk reduction benefits to outweigh the limitations imposed on future cash flows.

Alternative Hypothesis: The notional amounts of hedging derivatives will be negatively related to firm valuation when markets perceive the limitations imposed on future cash flows to outweigh their risk reduction benefits.

Trading derivatives, on the other hand, should act very differently from hedging derivative for two main reasons: a) They are not associated with risk reduction benefits and b) they produce revenues for those firms engaged in trading them. These derivatives clearly increase firm risk. With no other factors to consider a negative association between the coefficient of notional values of these derivatives and firm valuation would be expected. However, there are two important factors to consider when analyzing such derivatives, rarely mentioned in prior studies. The factors to consider are the facts that these derivatives generate a substantial amount of revenues for these firms and that, though not classified as hedging instruments, management employs risk reduction techniques within this category in an attempt to minimize the net exposure on either side of a position. Because these derivatives produce revenues, it is highly likely that their coefficient will be positively related to firm valuation. However, if markets view the risk introduced by these derivatives as offsetting any revenue benefits, then their coefficient may be either insignificant or negative depending on the market’s assessment of such risk. For these reasons the following hypotheses relating to trading derivatives are posited:

H₂: Due to their revenue generating potential, non-hedging derivatives will exhibit a positive relationship with changes in firm value. In other words, even if the derivative performs its function perfectly, this reduction in risk will cause the firm to shift downwards on the security market line to a lower risk/return profile.

H₃: After controlling for related trading revenues, the notional amounts of non-hedging derivatives will exhibit a negative relationship with changes in firm value, similar to hedging derivatives.

Finally, consistent with SFAS 133 classification and SFAS 161 requirement to disclose both the notional amounts of hedging derivatives and non-hedging derivatives separately, my final hypothesis will be the following:

H₄: The coefficient of the notional amounts of derivatives classified as hedging instruments as per SFAS 133 will be significantly different from the coefficient of those not classified as hedging instruments per SFAS 133.

Sample Data and Descriptive Statistics

The sample consists of 25 Bank Holding Companies which had both hedging derivatives, as classified by SFAS 133, and derivatives not classified as hedging derivatives during the time period studied. Those eliminated included banks that did not classify any of their derivatives as hedging instruments, those which did not comply with SFAS 161 starting in FY 2009, ADRs, and those who’s derivative holdings were considered negligible. Data is presented and examined on a quarterly basis beginning with the 1st quarter of 2009 and ending with the 4th quarter of 2019 for a total of 1,100 quarterly observations. Financial Data was obtained from the Compustat Bank Fundamentals Quarterly Database, Trading Revenue was obtained from the Federal Financial Institutions Examination Council (FFIEC) Central Data Repository's Public Data Distribution web site which provides data obtained from bank call reports, Stock Price data was obtained from CRSP, and the notional amounts of derivatives along with their fair values were obtained directly from the disclosure notes in the 10-Ks and 10-Qs filed by each bank for the SEC.

Table 2 presents descriptive statistics of some of the variables of interest in our study. Derivative holdings are concentrated on 5 banks which act as market makers. These banks hold 97% of all notional values held by BHCs. The remaining 3% is held within the remaining top 20 BHCs. For these 5 banks, revenues derived from derivative trading make up a big percentage of their business revenues. Interest Rate contracts comprise over 80% of the total notional values with Foreign Exchange Contracts coming in second at 12.4%. As seen below, trading derivatives comprise 99% of all notional values while derivatives classified as Hedging derivatives, per SFAS 133 standards, comprise only 1%. Risk management within the trading category does occur however as banks strive to reduce their net exposure on any side of a position.

Table 2 Descriptive Statistics Relating To Bank Holding Companies And Derivatives As Of December 31, 2019
Bank Name			Total Derivatives	Non- Hedging Derivatives Notionals	Hedging Derivatives Notionals	Market Cap	Derivatives Trading Revenue	Net Income (Loss)	Trading Rev as a % of NI
JP Morgan Chase			46,499,106	46,301,404	197,702	368,780	16,812	36,431	46%
Citigroup			40,820,866	40,660,193	160,673	163,580	6,232	19,280	32%
	Goldman Sachs		39,556,430	39,434,742	121,688	78,700	929	8,470	11%
	Morgan Stanley		32,513,056	32,437,531	75,525	73,930	1,932	9,040	21%
	Bank of America		30,395,057	30,140,687	254,370	279,730	3,535	27,430	13%
		Avg. for remaining 20 Banks	345,026	330,427	14,599	71,333	332	5,539	6%
		Total Sample	194,614,883	193,600,539	1,014,344	1,963,380	34,093	178,196	19%

Table 3 below shows how the 5 major market making banks derive a greater percentage of their total revenues from non-interest revenues which includes derivative trading revenues. These banks are also less dependent on Loans and Deposits which make up a lower percentage of Total Assets and Liabilities.

Table 3 Descriptive Statistics Relating To Bank Holding Companies And Major Sources Of Revenues As Of December 31, 2019
Bank Name	% of Non- Interest Revenue	% of Net Interest Revenue	Total Revenue	% of Loans to Assets	Total Assets	% of Deposits to Liabilities	Total Liabilities
JP Morgan Chase	50.5%	49.5%	115,627	35%	2,687,379	64%	2,426,049
Citigroup	36.2%	63.8%	74,376	35%	1,951,158	61%	1,757,212
Goldman Sachs	88.1%	11.9%	36,546	4%	992,968	21%	902,703
Morgan Stanley	88.7%	11.3%	41,419	15%	895,429	23%	812,732
Bank of America	46.4%	53.6%	91,244	40%	2,434,079	66%	2,169,269
Total for remaining 20 Banks	35.2%	64.8%	245,347	52%	4,299,494	82%	3,791,137

Table 4 reports the Pearson and Spearman correlations for the variables used in the subsequent regressions. Of interest is the high correlation between the following three explanatory variables: notional amounts of hedging derivatives (HD), notional amounts of non-hedging derivatives (NHD), and net fair values of derivatives (NFV). Though multicollinearity does not affect the overall explanatory power of the regression, it can obscure the parameters of each individual explanatory variable therefore some econometric techniques are employed to assuage the effects of multicollinearity in the subsequent section. Furthermore, multicollinearity of each specification used will be monitored by examining their variance inflation factors (VIF).

Table 4 Pearson And Spearman Correlations
	SP	BVPS	EPS	TRADRV	NFV	HD	NHD	ORTNH D
SP		0.90	0.80	0.60	0.75	0.69	0.70	0.07
BVPS	0.80		0.71	0.56	0.77	0.63	0.77	0.20
EPS	0.80	0.64		0.55	0.62	0.60	0.58	-0.05
TRADRV	0.53	0.44	0.42		0.72	0.66	0.69	0.00
NFV	0.26	0.57	0.19	0.20		0.89	0.95	-0.01
HD	0.23	0.53	0.19	0.23	0.70		0.94	0.16
NHD	0.26	0.41	0.18	0.54	0.47	0.55		0.10
ORTNHD	0.13	0.20	0.05	-0.11	0.03	0.15	0.06

Pearson Correlations are shown above the diagonal and Spearman Correlations are shown below the diagonal.

Empirical Analysis and Results

Prior research has developed various models specific to the banking industry. These models, however, tend to work best for studies related to interest rate margins. Because the sample used in this study is heterogeneous, with many of the sample banks generating the bulk of their financials from fee related revenue, a more general model is used. Following Barth & Clinch (1998), An enhanced version of the Ohlson Model (1995) is estimated to evaluate the value relevance of the data studied. The model used was the following:

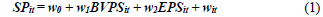
In this model SP represents share price and it is regressed on Book Value of Equity per Share and Earnings per Share. The scaling on a per share basis should help alleviate bias introduced by size as bank sizes vary considerably. In other words, scaling on a per share basis may help with omitted variable bias. Similar model, detailed in Table 5, incorporating notional amounts for both hedging and non-hedging derivatives as well as other explanatory variables are estimated to find the best fitting model free of econometric issues. Table 5 presents the results obtained for 6 of these models 2. It starts off with the basic specification whereby stock prices are regressed on book value per share and earnings per share to verify the validity of my data. If the data proves not good enough for this basic earnings capitalization model then it would be imprudent to proceed by adding variables to this model and other econometric techniques would have to be explored. This model will also serve as a basis of comparison of subsequent models. Model 1 shows that book value per share and earnings per share combined explain approximately 86% of the variation in stock prices for my sample data. Furthermore, the mean VIF of this model is 2.04 indicating multicollinearity is not an issue. In model 2, the two main variables of interest, notional amounts of hedging (HD) and non-hedging derivatives (NHD), are added. Results show that the addition.

Other models examined but excluded from the table above include a fixed effects year model, a model using sales growth as a proxy for omitted variables, and many others of notional amounts of hedging derivatives and non-hedging derivatives help improve the explanatory power of the earnings capitalization model from 86% to 89.4% as expressed by the adjusted R2. All variables are significant at the 5% level of significance. Results show that, consistent with the alternative to our first hypothesis, notional amounts of hedging derivatives are negatively related to changes in stock prices. This is consistent with the theory that, while markets may view such derivatives as risk reducers, they come at a price. The price is limitations on future expected cash flows thus causing the negative associations. This is consistent with financial theory that stipulates that risk and return are inversely related and that, for firms that are efficiently priced, risk cannot be reduced without sacrificing potential future returns. Furthermore, we see that the notional amounts of non-hedging derivatives are positively related to changes in firm valuation consistent with my second hypothesis. However, this positive relationship may be related to the revenue generating capacity of these derivatives which, unlike hedging derivatives, generate revenues for these firms at high gross margins. While results are consistent with my hypotheses, there is one major flaw to this model, note that this model has a mean VIF of 6.46.

This high VIF is driven by the high multicollinearity between the notional amounts of hedging and non-hedging derivatives. Model 3 controls for trading revenue by adding this variable to the right hand side model 2. Results are consistent with prior expectations. Once again notional amounts of hedging derivatives are significantly negatively related to changes in firm value at all confidence levels. Trading revenues, the new variable, is significantly positively related to changes in firm value at all confidence levels as well. Notional amounts of non-hedging derivatives continue to be positively related to changes in firm value. This is not consistent with my third hypothesis, which indicated that once the revenue generating power of these derivatives are controlled for, they should exhibit a negative relationship with changes in firm value. These results, however, may be affected by the high mean VIF of this model. While the adjusted R2 of model 3 improves that of model 2 from 89.4% to 89.9% and the average VIF is reduced from 6.46 to 5.77, this model still has a very high VIF. In particular, when looking at the individual explanatory variables within this model, results show that the notional amounts of hedging and non-hedging derivatives have VIFs of 11 and 9.2 respectively. Net fair values of derivatives were added in model 5. Adding this variable increased the explanatory power of the model to 90.5% but at a cost of increasing the VIF to 8.62, an unacceptable level to draw any inferences on individual coefficients. In model 6, the intercept is permitted to vary by individual BHC using a fixed firm effects model. Once again the mean VIF of this model was simply too high to draw any reliable inferences.

In an attempt to assuage the multicollinearity issues found in my 3rd specification, the notional amounts of non-hedging derivatives are orthogonalized with their related trading revenues. This is done by replacing the notional amounts of hedging derivatives in model 3 with the residuals of the following regression:

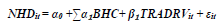
By doing so, any redundancies between these two variables in explaining changes in firm valuation are eliminated. A look at the correlation matrix shows that the correlation of the new variable (ORTNHD) and trading revenues is 0. This simple econometric technique can help assuage the multicollinearity issues experienced in the prior models and help us draw more reliable inferences on the results. Model 4 in Table 5 shows us the results of this specification. The first thing to note is that the mean VIF is now reduced to 1.76. Furthermore, a look at the VIF of each individual explanatory variable shows that none of the explanatory variables has a VIF greater than 4.5. Thus Model 4 is the most econometrically sound of all and the one from which the paper will draw its final conclusions. Consistent with the alternative to my first hypothesis, and with the results of all the other models, this model shows that the relationship between hedging derivatives and firm valuation is significant and negative at all levels of confidence. This supports the theory that the use of hedging derivatives cause a downward shift of the Security Market Line (SML) for firms using derivatives as hedging instruments. A portion of this downward shift can also be attributed to skepticism on the efficacy of these derivatives. Results also show that, once notional amounts of non-hedging derivatives are orthogonalized to remove the revenue effect, their relationship with firm valuation becomes significant and negative at the 95% level of confidence. This is consistent with the paper’s third hypothesis which attributes any positive relationship between trading derivatives and firm value to their revenue generating effect. The results for the remaining variables are all as expected and significant at all levels of confidence. Model 4 helps explain 88.4% of the variation in firm value as expressed by stock price changes. Finally, a comparison of the coefficients hedging derivatives and non-hedging derivatives shows that they are significantly different, supporting the need to report these separately as investors give each classification a different weight in firm valuation. In fact, once trading revenues are controlled for, results show that markets view non-hedging derivatives as riskier than hedging derivatives as evidenced by their greater negative coefficient to firm value.

Table 5 Model Specification Results
#	Specification	α₀	BVPS	EPS	HD	NHD	ORTNHD	TRADRV	NFV	adj. R2	Mean VIF
(1)	SPit = α0 + β1BVPSit + β2EPSit + εit	1.868	0.721	9.022					0.860		2.04
	P Values	0.096	0.000	0.000
(2)	SPit = α0 + β1BVPSit + β2EPSit + β3HD + β4NHD + εit	4.089	0.912	8.673	-0.002	0.0007			0.894		6.46
	P Values	0.000	0.000	0.000	0.000	0.000
(3)	SPit = α0 + β1BVPSit + β2EPSit + β3HD + β4NHD + Β₅TRADRV + εit	3.469	0.924	7.868	-0.004	0.0006		8.649	0.899		5.77
	P Values	0.002	0.000	0.000	0.000	0.000		0.000
(4)	SPit = α0 + β1BVPSit + β2EPSit + β3HD + β4ORTNHD + Β₅TRADRV + εit	-0.721	0.928	7.373	-0.001		-0.162	12.891	0.884		1.76
	P Values	0.514	0.000	0.000	0.000		0.033	0.000
(5)	SPit = α0 + β1BVPSit + β2EPSit + β3HD + β4NHD + Β₅TRADRV + β₆NFV + εit	4.923	0.903	7.320	-0.003	0.0002		6.2590	0.181    0.905		8.62
	P Values	0.000	0.000	0.000	0.000	0.065		0.004	0.000
(6)	SPit = α0 + ∑ α₁ BHC + β2EPSit + β2EPS it + β3HD + β4NHD + εit	3.355	0.596	5.558	-0.005	0.0005			0.950		28.39
	i = 1	0.125	0.000	0.000	0.000	0.053

Where SP is share price; BVPS is book value per share; EPS is earnings per share; HD is the notional value of derivatives classified as hedging derivatives per share; NHD is the notional value of derivatives not classified as hedging derivatives per share; TRADRV is the derivatives trading revenues; NFV is the net fair value of derivatives as presented on the face of the statements; ORTNHD is the notional amounts of non-hedging derivatives after being orthogonalized with related trading revenues. Number of observations = 1,100. The FE model controls for common variables within each BHCs 44 quarterly sample periods by creating dummy variables for each bank (except the base). Therefore, this model will contain 44 different α₁ for each bank excluding the base bank

Conclusion

In conclusion, this paper attempts to contribute towards the literature on the value relevance of derivatives disclosures. Taking advantage of new disclosure requirements under SFAS 133 and SFAS 161 and of an increased market awareness of the use of derivatives after the 2008 financial crisis, this paper re-examines the relationship between derivatives and firm valuation. Results show that hedging derivatives are negatively correlated to firm valuation. This implies that while management may have achieved its purpose of reducing certain risks, it does so at the expense of curtailing potential positive cash flow thus leading to the negative association found.

Unlike hedging deriveratives, non-hedging derivatives not only introduce risk but also increase cash flows in the form of trading revenues. This helps explain the positive correlation found by many prior studies, between firm valuation and notional amounts of non-hedging derivatives (mostly known as trading derivatives). This study confirms the positive relationship between notional amounts of non-hedging derivatives and firm valuation but shows that this relationship is driven mostly by their revenue generating potential. Controlling for their revenue generating potential, results show that these derivatives lead to a market discount on firm value.

SP is share price; BVPS is book value per share; EPS is earnings per share; HD is the notional value of derivatives classified as hedging derivatives per share; NHD is the notional value of derivatives not classified as hedging derivatives per share; TRADRV is the derivatives trading revenues; NFV is the net fair value of derivatives as presented on the face of the statements; ORTNHD is the notional amounts of non-hedging derivatives after being orthogonalized with related trading revenues. Number of observations = 1,100. The FE model controls for common variables within each BHCs 44 quarterly sample periods by creating dummy variables for each bank except the base. Therefore, this model will contain 44 different α_₁ for each bank excluding the base bank.

References

Ahmed, A.S., Kilic, E., & Lobo, G.J. (2006). Does recognition versus disclosure matter? Evidence from value relevance of banks' recognized and disclosed derivative financial instruments.The Accounting Review,81(3), 567-588.

Indexed at, Google Scholar, Cross Ref

Barth, M.E. (1991). Relative measurement errors among alternative pension asset and liability measures.Accounting Review, 433-463.

Indexed at, Google Scholar

Barth, M.E., & Clinch, G. (1998). Revalued financial, tangible, and intangible assets: Associations with share prices and non-market-based value estimates.Journal of Accounting Research,36, 199-233.

Indexed at, Google Scholar, Cross Ref

Duangploy, O., & Helmi, D. (2002). Analysis of derivatives'unrealized gains/losses from pre-sfas 133 disclosures: banking industry.Academy of Accounting and Financial Studies Journal,6(3), 1.

Indexed at, Google Scholar

Riffe, S. (1997). The valuation of off-balance sheet financial instrument disclosures in the banking industry: In Derivatives, regulation and banking industry: Advances in Finance, Investment and Banking Services. Amsterdam, B Schachter (ed.), 93-121. Holland.

Seow, G.S., & Tam, K. (2002). The usefulness of derivative-related accounting disclosures.Review of Quantitative Finance and Accounting,18(3), 273-291.

Indexed at, Google Scholar, Cross Ref

Skinner, D.J. (1996). Are disclosures about bank derivatives and employee stock options ‘value-relevant’?.Journal of Accounting and Economics,22(1-3), 393-405.

Indexed at, Google Scholar, Cross Ref

Venkatachalam, M. (1996). Value-relevance of banks' derivatives disclosures.Journal of Accounting and Economics,22(1-3), 327-355.

Indexed at, Google Scholar, Cross Ref

Wang, L., Alam, P., & Makar, S. (2005). The value-relevance of derivative disclosures by commercial banks: A comprehensive study of information content under SFAS Nos. 119 and 133.Review of Quantitative Finance and Accounting,25(4), 413-427.

Indexed at, Google Scholar, Cross Ref

Received: 27-Feb-2022, Manuscript No. AAFSJ-22-11389; Editor assigned: 01-Mar-2022, PreQC No. AAFSJ-22-11389(PQ); Reviewed: 15-Mar-2022, QC No. AAFSJ-22-11389; Revised: 05-Apr-2022, Manuscript No. AAFSJ-22-11389(R); Published: 12-Apr-2022