Keywords

Value at Risk, Downside Risk, Kupiec Point of Failure Test, Christofferson Test, Risk Management.

Introduction

It is really difficult to manage the downside risk when the financial market around the world is fluctuating, especially in emerging markets, and to minimize the downside risk; everyone recognizes the importance of managing it. Risk management provides various models or tools for managing downside risk. The different ways of measuring risk that have emerged in financial markets in recent decades raise concerns about their validity. The most advanced and preferred risk management model has to be Value at Risk (VaR) because it is simple to understand and easy to interpret. Value at Risk (VaR) is the primary measure of downside risk. Its the most prominent risk measurement method often used by investors, institutional investors, FIIs, fund managers, hedgers, risk managers, regulators, policymakers, and other participants. Over the last decade, Value at Risk (VaR) has evolved as one of the most important risk measuring approaches in finance. When implementing Value at Risk (VaR) systems, it attempts to anticipate future asset prices using prior market data, which may or may not correctly reflect the market environment in the future. As a result, Value at Risk (VaR) models are only effective if they appropriately forecast future risk. To ensure that the results of Value at Risk (VaR) estimates and forecasts for any stock indices are consistent and accurate, the models should regularly be validated for those stock indices using correct statistical processes. One can never be sure that the Value at Risk (VaR) approach produces reliable risk assessments without effective model validation. The topic is particularly relevant in the emerging market, where the volatility is always higher than the advanced countries' markets. The accuracy of the Value at Risk (VaR) estimates and forecasts in emerging markets is always an important issue, so backtesting has been used for this purpose in this study. Testing the Value at Risk (VaR) forecasting power in emerging market are very important for risk managers, investors, policymakers, institutional investors, FIIs, fund managers, hedgers, financial and non-financial institutions, regulators, and other participants.

Backtesting is a process of comparing an actual loss with forecasted loss calculated through value at risk from past data, and it compares statistical confidence level with the number of exceptions. If exceptions are too high or low compared to the chosen significance level (we selected 5 percent), the model overestimates or underestimates volatility. If exceptions match the significance level, then the Value at Risk (VaR) model estimation in these stock indices is valid. In the present study, two most commonly used backtesting approaches, namely the Kupiec “Point of Failure Test” and “Christoffersen Test,” have been used to validate the Value at Risk (VaR) model in BRICS. The study estimated and forecasted the Value at Risk (VaR) for BRICS countries' stock markets and validated Value at Risk (VaR) results through Kupiec Point of Failure Test” and “Christoffersen Test”. No paper in the literature has studied the backtesting of any risk measure for such a long time and contributed to the body of knowledge on validation of Value at Risk (VaR) estimation forecasting power for BRICS economies. The Value at Risk (VaR) model was only backtested because it is the most popular and commonly utilized risk measurement technique. Other lesser-known risk metrics can be backtested by future researchers like ES, weighted ES, Generalized quantile, Beyond VaR, Limited VaR, and the like. Also, they can use other backtesting techniques. Thus, the paper contributed to the body of knowledge by investigating the validation of the Value at Risk (VaR) model as a risk management technique in BRICS stock indices. To the best of the Authors' knowledge, no prior study has contributed to the body of knowledge on the acceptability of the VaR model as a risk management tool for any country indices that too for such a long period. The study's findings have practical implications for investors, institutional investors, FIIs, fund managers, hedgers, risk managers, regulators, policymakers, and other participants. These participants were expected to benefit considerably from the empirical findings of this study. These participants can use Value at Risk (VaR) as a risk-management tool for financial control, reporting, investment, and risk management-related decisions.

The rest of the paper is organized as follows:

1. Section 2 presents the objective of the study;
2. Section 3 provides the research methodology section;
3. Section 4 discusses the results and findings; and,
4. Section 5 gives us the conclusion, followed by the reference section.

Objectives

An attempt has been made to achieve the following main objectives:

1. To validate the Value at Risk (VaR) model as a risk management tool in BRICS economies.
2. To check if the Value at Risk (VaR) model provides reliable estimates in BRICS economies.
3. To help stock market stakeholders in investment and financial risk management-related decisions.

Research Methodology

The study uses weekly closing price data of BRICS countries' leading stock indices from April 1996 to March 2021 taken from investing.com. The interpolation method performed in Stata 16 software was used for filling the few missing observations in this data. The main stock indices selected for the study are Brazil (BOVESPA Index), Russia (RTS Index), India (NIFTY 50 Index), China (SSE Composite Index), and South Africa (FTSE 100 Index). The log or compounded return is calculated from weekly closing price data in R software by using the following formula:

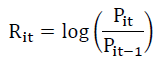
where;

Rit stands for log difference return at time t,
Pit and Pit-1 stand for two successive weekly closing prices of the selected ith stock exchange.
The study used log difference returns as they are symmetrical and preferred for various advance financial calculations (Danielsson, 2011). The study performs the analysis using R software.

Descriptive Statistics And Unit Root Test

Descriptive statistics is an important tool for defining and explaining the fundamental aspects of a data collection. It is used to calculate the centre, spread (variability), and shape of the data. This study uses mean, standard deviation, skewness, and kurtosis to assess the behaviour of the gathered data set. Before applying any econometric model to the data, it is required to investigate the unit root and whether or not cointegration occurs. The unit root test is used to determine if time-series data is stationary, that is, whether it travels around a constant long-run mean, whether covariance is constant or time-fixed, and whether the theoretical correlogram diminishes as lag length grows (Asteriou & Hall, 2007). In this study, the first instance line graph is employed to identify volatility clusters. The data series' unit root is then validated using the Augmented Dickey-Fuller (ADF) and Philips-Perron tests. The ADF test use the following model to test H₀: γ= 0. If the ADF test statistics are less than the critical value, the H₀ is rejected, and we may infer that the series is stationary.

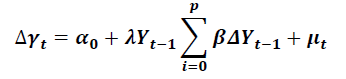
In addition, the current study employs another unit root test, the Phillips–Perron (PP) test, to evaluate the null hypothesis H₀: β=0 The H0 is rejected if the PP test statistics is less than the crucial value, indicating that the series has no unit root.

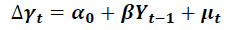
Results and Discussions

Descriptive Statistics

Tables 1 and 2 show the summary of descriptive results of the series for the reference period, and it is clear from Table 1 that comparatively, there is a maximum standard deviation in the Russian stock exchange (RTS Index (RTSI.ME).

Table 1 Summary Of Descriptive Statistics Of Closing Prices Of Brics Stock Indices
Country	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.	st dev	kurtosis	skewness
IBOVESPA (^BVSP)(b)	5016	14862	48535	44758	62930	125077	28899.86	2.4496	0.446406
RTS Index (RTSI.ME)(r)	38.81	373.83	1020.46	960.33	1399.69	2478.87	586.8396	2.0625	0.148539
NIFTY 50 (^NSEI)	808.2	1323.7	4523.4	4872.8	7783.8	15163.3	3627.958	2.3372	0.644596
SSE Composite Index (000001.SS)(C)	587.0	1504.0	2192	2302	2979	5903	939.3984	3.5421	0.692012
FTSE 100 (^FTSE)(sa)	3991.0	8771.0	24278	25641	44028	62789	16795.26	1.6329	0.30361

Table 2 Descriptive Statistics Of Stock Market Return Of Brics Stock Indices
Country	Min.	1st Qu.	Median	Mean	3rd Qu.	Max	st dev	kurtosis	skewness
IBOVESPA (^BVSP)(b)	-0.250585	.020156	.004896	.00240 6	.026787	.217 57	.04159 6	7.388755	-0.608774
RTS Index (RTSI.ME)(r)	-0.341144	.023196	.004698	.00217 2	.030691	.341 876	.05802 9	8.185776	-0.435805
NIFTY 50 (^NSEI)	-0.173755	.015466	.003965	.00204 7	.019742	.143 568	.03168 8	5.712919	-0.32000
SSE Composite Index (000001.SS)(C)	-0.226293	.017048	.00237	.00136 7	.019119	.160 587	.03367 1	6.679132	-0.259518
FTSE 100 (^FTSE)(sa)	-0.169327	.013769	.002728	.00180 5	.017772	.179 208	.02913 7	7.193702	-0.294176

The return series of these indices are negatively skewed, and the distribution is leptokurtic (with fat and long-tail) as all of these kurtosis values are greater than three. Thus, both kurtosis and skewness result shows that the data is not normal. The Jarque Bera test results presented in Table 3 support these results. The p-value for each return series is less than 1%, thereby discrediting the null hypothesis of the Jarque Bera test.

 

Table 3 Jarque Bera Test Results
H0: Data is Normally Distributed (skewness =0 and kurtosis=3)
	Brazil	Russia	India	China	South Africa
X-squared	1126.2	1501.3	421.82	749.52	973.63
Df	2	2	2	2	2
p-value	< 2.2e-16	< 2.2e-16	< 2.2e-16	< 2.2e-16	< 2.2e-16

Unit Root Tests

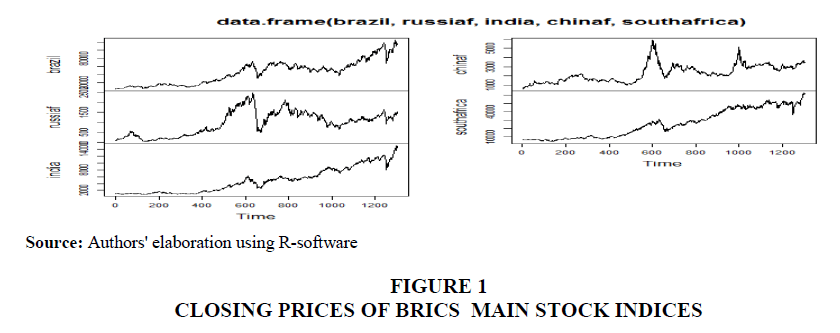
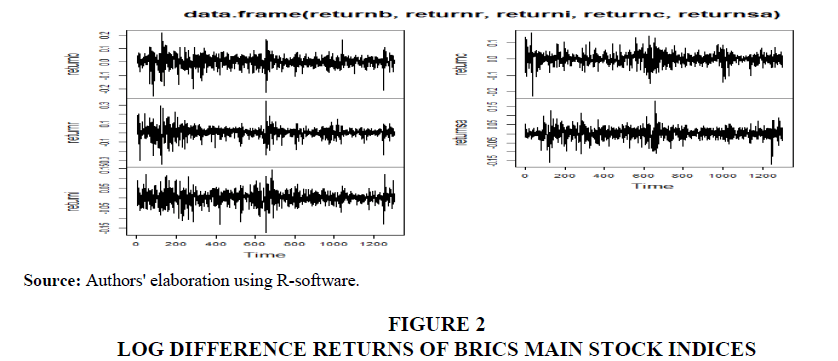
Before conducting the formal unit root tests, it would be in the fitness of things to have a rough idea about the stationarity by developing the line graph of BRICS stock market indices closing prices and log difference returns of each country in the BRICS bloc. These are shown in figure 1 and figure 2.

The augmented dickey fuller test (Dickey & Fuller, 1979) and Phillips perron test (Phillips & Perron, 1988) were applied to check stock index return series stationarity. The PPs-test was employed because there is heteroskedasticity in the error terms. The presence of a unit root test is a null hypothesis for both these tests. As presented in Table 4, both the test result showed that all these series are non-stationary because the p-value of ADF statistics and PP statistics for all stock returns of all BRICS countries is more than the assumed level of significance (p-value >.05). Hence, one can conclude that each BRICS nation's stock market returns series has unit root at level. However, all the return series of BRICS countries' stock markets are found to be stationarity at first difference level I(1) under both the tests, as the P-vlaue found to be < .01 for each return series.

Table 4 Results Of Unit Root Tests
Stock Returns	Augmented Dickey-Fuller Unit root Test (ADF-test)			Phillips-Perron Unit root Test (PPs-test)
	Lags	Test-statistics	P-values	Lags	Test-statistics	P-values
Brazil
Level	10	-2.6331	0.3103	7	-17.365	0.1411
1st Difference	10	-11.669	0.01*	7	-1467.2	0.01*
Russia
Level	10	-2.4033	0.4076	7	-9.4034	0.5852
1st Difference	10	-10.263	0.01*	7	-1331.1	0.01*
India
Level	10	-2.0173	0.571	7	-10.217	0.5398
1st Difference	10	-11.019	0.01*	7	-1287.0	0.01*
China
Level	10	-3.4027	0.05297	7	-15.569	0.2413
1st Difference	10	-9.581	0.01*	7	-1268.5	0.01*
South Africa
Level	10	-2.792	0.243	7	-18.396	0.09567
1st Difference	10	-10.968	0.01*	7	-1332.4	0.01*

Evaluating Var Forecast Validation: Unconditional And Conditional Coverage Tests

Investors or institutions keenly monitor the performance of emerging markets stock markets because these markets generate healthy returns compared to the developed markets. Consequently, the risk of investment in these stock markets is obviously more. Besides, there is a significant increase in capital inflow in emerging markets due to greater upside deviation offered by these emerging markets, including South Africa (McMillan & Thupayagale, 2010). These markets have a higher risk and conditional volatility as compared to advanced countries' stock markets (Bekaert & Harvey, 2003; Santis & Imrohoroglu, 1997), not due to world risk factors but due to local risk factors. Investors, FIIs, or foreign portfolio investments prefer emerging markets to diversify their portfolios (Vo and Ellis, 2018) as returns from emerging stock markets are more volatile and give higher average returns (Bekaert & Wu, 2000). The Value at Risk (VaR) models were constructed to assess the possible negative loss of a risky financial asset or investment. In statistical terms, Value at Risk (VaR) refers to the quantile of a probability distribution function. The concept of Value at Risk (VaR) refers to the maximum amount of money that may be lost on a portfolio or a single asset with a certain level of confidence owing to market risk exposure over a specific period.(Hendricks (1996); Jorion (2007) defined Value at Risk (VaR) as “the worst loss over a target horizon such that there is a low, prespecified probability that the actual loss will be larger,” and Dowd, K. (1998) defined it as “the value at risk (VaR) is the maximum expected loss over a given horizon period at a given level of confidence.” These definitions comprise the time horizon expressed daily, weekly, monthly, or annually and the level of confidence, which can be 99.9%, 99%, or 95% (Jorion, 2007). The level of confidence, the length, and the potential loss of value are the three most important components of Value at Risk (VaR). The reference period captures the span of information gathered in the Value at Risk (VaR) measure, and the probability of the expected minimum loss is the confidence level. Value at Risk (henceforth VaR) is generally accepted as a measure of risks to which financial institutions are exposed. Value at Risk (VaR) has evolved as one of the most important risks measuring approaches (Bai & Lam, 2022). There are various methods for estimating Value at Risk (VaR) but Historical simulation (Wu & Thanyaluckpark, 2019) and Historical method is producing more accurate estimates (Salem, et al., 2022). When implementing Value at Risk (VaR) systems, it attempts to anticipate future asset prices using prior market data, which may or may not correctly reflect the market environment in the future. As a result, Value at Risk (VaR) models are only effective if they correctly forecast future risk. For this purpose, Backtesting technique is used.

After understanding the Value at Risk (VaR) of stock markets, an attempt is made to examine the forecast power of the Value at Risk (VaR) model by using the well-recognized backtests. Backtesting is the process of comparing an actual loss to a Value at Risk (VaR) value calculated from past data. It ensures an accurate assessment of volatility. Assuming a 5% significance level, five-day exceptions occur once every 100 days on average; It examines whether the statistical confidence level corresponds to the number of exceptions. If the exceptions are too high or low compared to the chosen significance level, the model overestimates or underestimates volatility. If the exceptions match the significance level, the volatility estimation is valid. The two types of backtesting approaches are conditional and unconditional, with the former computing and comparing the number of exceptions with the degree of significance. While the latter tests the exceptions' dependence and calculates and compares the number of exceptions with the significance level (Jorion, 2007). Unconditional coverage and independence properties should be included in a good estimating model (Jorion, 2007; Campbell, 2005; Christoffersen et al., 2004). Unconditional tests are simple to implement since they do not take into account the timing of exceptions, whereas conditional coverage tests do (Jorion, 2007). It is being said that a model is as good as its backtest; therefore, in order to evaluate the quality of the model, it is always recommended to intensively backtest the same (Einhorn & Brown, 2008). Backtesting is important to risk managers, investors, policymakers, institutional investors, FIIs, fund managers, hedgers, financial and non-financial institutions, regulators, and other participants. With this test, we ensure that model provides an accurate assessment of volatility. The main purpose of this research is to validate the Value at Risk (VaR) model as a risk management technique in the BRICS stock indices.

We employed the most common and important backtests to validate the Value at Risk (VaR) model, namely the Kupiec point of failure and Christofferson tests. Kupiec's test merely analyses the number of actual losses with estimated losses, whereas Christofferson also takes into account the independence of exceptions. By taking into consideration the timing of exceptions, Conditional coverage tests overcome the drawback of Unconditional coverage tests. The null hypothesis for both tests is that the model is good. The Rollgarch package in R software applies both the unconditional coverage test (Kupiec), (Kupiec, 1995) and conditional coverage test (Christofferson) tests (Christoffersen et al., 2004). The study used historical data from April 1996 to March 2021. It is recommended to start backtesting after skipping a few initial years to overcome the problem of the non-converged estimation window; therefore, the study started backtesting from 2001 to 2021. The Value at Risk (VaR) is calculated at a 5% significance level for all BRICS stock indices. The study reestimated the Value at Risk (VaR) estimates after every year using the “moving” period of estimation method and “Hybrid solver” algorithm for specification. As presented in Table 5, the test results failed to reject the null hypotheses of both the tests because test statistics are less than critical values; as such, it is concluded that the Value at Risk (VaR) model has the power to give an accurate estimate or forecasts of volatility.

Table 5 Unconditional And Conditional Coverage Test
VaR Backtest Report	Brazil	Russia	India	China	South africa
Model	sstd(VaR)	sstd(VaR)	sstd(VaR)	sstd(VaR)	sstd(VaR)
Backtest Length	783	783	783	783	782
Data
Alpha (a)	5%	5%	5%	5%	5%
Expected Exceed	39.2	39.2	39.2	39.2	39.2
Actual VaR Exceed	33	43	34	50	37
Actual	4.2%	5.5%	4.3%	6.4%	4.7%
Unconditional Coverage (Kupiec Point of Failure) Test
Null-Hypothesis (H0)	Correct Exceedances	Correct Exceedances	Correct Exceedances	Correct Exceedances	Correct Exceedances
LR.uc Statistic	1.072	0.387	0.745	2.921	0.127
LR.uc Critical	3.841	3.841	3.841	3.841	3.841
LR.uc p-value	0.301	0.534	0.388	0.087	0.722
Reject H0	NO	NO	NO	NO	NO
Conditional Coverage (Christoffersen) Test
Null-Hypothesis	Correct Exceedances &	Correct	Correct	Correct	Correct
(H0)	Independence of	Exceedances	Exceedances	Exceedances	Exceedances &
	Failures	&	&	&	Independence of
		Independence	Independence	Independenc	Failures
		of Failures	of Failures	e of Failures
LR.cc Statistic	4.75	1.459	2.096	5.224	0.164
LR.cc Critical	5.991	5.991	5.991	5.991	5.991
LR.cc p-value	0.039	0.482	0.351	0.073	0.921
Reject H0	NO	NO	NO	NO	NO

Conlcusion

This study examined the applicability of the Value at Risk (VaR) model in BRICS nations' stock returns as a risk management tool through backtesting. The study verified Value at Risk (VaR) forecasting in estimating the risk using backtesting. The weekly stock return series of the BRICS nations were not normally distributed and was found to be stationary at first difference. The Unconditional and Conditional Coverage Tests, i.e., Kupiec point of failure and Christofferson tests, revealed that Value at Risk (VaR) forecast models as a risk management tool are accurate. No study in the literature has investigated the performance of the Value at Risk (VaR) model in specific countries' stock indices. Backtesting the Value at Risk (VaR) forecasts for countries' stock indices has received very little attention in the past. The study contributed to the body of knowledge by investigating the validation of the Value at Risk (VaR) model as a risk management technique in BRICS main stock indices, which has not been studied in prior studies. The Value at Risk (VaR) model was only backtested because it is the most popular and commonly utilized risk measurement technique. Other, lesser-known risk metrics can be backtested by future researchers like ES, weighted ES, Generalized quantile, Beyond VaR, Limited VaR, etc., and backtesting techniques. In order to gain a better understanding, the authors believe that future studies should be extended to other trade blocs and countries.

References

Asteriou, D., & Hall, S.G. (2007). Applied Econometrics: a modern approach, revised edition.Hampshire: Palgrave Macmillan,46(2), 117-155.

Indexed at, Google Scholar

Bai, X., & Lam, J. S.L. (2022). Portfolio value‐at‐risk estimation for spot chartering decisions under changing trade patterns: A copula approach.Risk Analysis.

Indexed at, Google Scholar, Cross Ref

Bekaert, G., & Harvey, C.R. (2003). Emerging markets finance.Journal of empirical finance,10(1-2), 3-55.

Indexed at, Google Scholar, Cross Ref

Bekaert, G., & Wu, G. (2000). Asymmetric volatility and risk in equity markets.The review of financial studies,13(1), 1-42.

Indexed at, Google Scholar, Cross Ref

Campbell, S.D. (2005). A of backtesting and backtesting procedures. The Journal of Risk, 9(2), 1–17.

Indexed at, Google Scholar

Christoffersen, P., & Pelletier, D. (2004). Backtesting value-at-risk: A duration-based approach.Journal of Financial Econometrics,2(1), 84-108.

Indexed at, Google Scholar, Cross Ref

Danielsson, J. (2011).Financial risk forecasting: the theory and practice of forecasting market risk with implementation in R and Matlab. John Wiley & Sons.

Indexed at, Google Scholar

Dickey, D.A., & Fuller, W.A. (1979). Distribution of the estimators for autoregressive time series with a unit root.Journal of the American statistical association,74(366a), 427-431.

Indexed at, Google Scholar, Cross Ref

Einhorn, D., & Brown, A. (2008). Private profits and socialized risk.Global Association of Risk Professionals,42, 10-26.

Google Scholar

Hendricks, D. (1996). Evaluation of value-at-risk models using historical data.Economic policy review,2(1), 39-70.

Indexed at, Google Scholar, Cross Ref

Jorion, P. (2007) ‘Value_at_Risk,_3rd_Ed.__The_New Benchmark for managing financial risk.’

Kupiec, P.H. (1995). Techniques for Verifying the Accuracy of Risk Measurement Models. The Journal of Derivatives, 3(2), 73-84.

Indexed at, Google Scholar, Cross Ref

McMillan, D., & Thupayagale, P. (2010). Evaluating stock index return value-at-risk estimates in South Africa: Comparative evidence for symmetric, asymmetric and long memory GARCH models.Journal of Emerging Market Finance,9(3), 325-345.

Indexed at, Google Scholar, Cross Ref

Phillips, P.C., & Perron, P. (1988). Testing for a unit root in time series regression.Biometrika,75(2), 335-346.

Indexed at, Google Scholar, Cross Ref

Salem, A. Ben, Safer, I., & Khefacha, I. (2022). Value-at-Risk (VAR) Estimation Methods: Empirical Analysis based on BRICS Markets.

Indexed at, Google Scholar

Santis, G.D. (1997). Stock returns and volatility in emerging financial markets.Journal of International Money and finance,16(4), 561-579.

Indexed at, Google Scholar, Cross Ref

Wu, D., & Thanyaluckpark, C. (2019). Valueat Risk Performance in BRICS countries. In2019 4th IEEE International Conference on Cybernetics (Cybconf)(pp. 1-5). IEEE.

Indexed at, Google Scholar, Cross Ref

Received: 23-Sep-2022, Manuscript No. AAFSJ-22-12602; Editor assigned: 24-Sep-2022, PreQC No. AAFSJ-22-12602(PQ); Reviewed: 07-Oct-2022, QC No. AAFSJ-22-12602; Revised: 12-Oct-2022, Manuscript No. AAFSJ-22-12602(R); Published: 19-Oct-2022