Keywords

Location Selection, Multi-criteria analysis, AHP, SAW, Promethee II, Sensitivity Analysis.

Introduction

In this paper, facility location selection problem is considered. The long-term planning of manufacturing organizations is greatly influenced by facility location decisions. Medical centers chosen incorrectly may result in the absence of qualified trainers for work and the absence of medical tools for blood centers, the absence of medical tools for blood centers, insufficient transportation facilities for patients, an increase in travel expenses or the organization could be negatively affected by political and societal interference. The best location for medical centers should be chosen by the decision maker to ensure both performance and flexibility to accommodate the necessary future changes. This decision support system uses the PROMETHEE II and SAW (Simple Addictive Weighting) methods in the process of selecting the best location and the results are compared. The ability of these methods to solve decision-making problems with multiple conflicting criteria and alternatives has been observed.

The reminder paper is laid out in the following order: PROMETHEE II and SAW techniques are discussed in section 2, along with formulas and relationships. The impact of sensitivity analysis on MCDM models is proposed in Section 3, which is the most important part of the paper. The accuracy of the proposed model is examined through a numerical example presented in Section 4. In section5, the results are discussed.

Methods

Different techniques (Agrawal et al., 2010) have already been used by previous researchers to solve the issue of facility location selection. Using complex mathematical formulations, most of those techniques neglect qualitative information about criteria values. The problem (Siahaan et al., 2017) often faced by the decision makers is the injustice in choosing a decision which lead to difficulties. Using manual work (Bertsimas et al., 2006) for location selection problems includes disadvantages such as high cost and the fact that well- trained professionals are required in the decision making process. A fuzzy TOPSIS method (Yong, 2006) is used for solving plant location selection decision-making problems in linguistic environment. Fuzzy TOPSIS method (Önüt et al., 2008) is used to solve the solid waste transshipment site selection problem and AHP is used in determining criteria weights. TOPSIS method (Amiri et al., 2009) is used for selecting the best location along with heuristics based on fuzzy goal programming. Topsis (Ghose, 2021) is used in site selection process for steel industry.

AHP method (Ishak et al., 2009) was proved as an efficient method to handle complicated decision making problems. It analyses the data that has been collected and it can speed up the process by identifying and weighing available selection criteria.

The Analytic Hierarchy Process (Mani, 2014) is a decision-making process for determining weights in multi-criteria decision-making. It was first introduced by mathematician Saaty in 1980. AHP is a reliable method for calculating criteria weights. However, the AHP method was not appropriate if used for the ranking process because the calculation process does not distinguish between costs and benefit data. So, it was only used for the weighing process. This SAW method (Taherdoost et al., 2023a). In order to determine the ranks of the alternatives, the SAW method utilizes the concept of additive property. This Multi-criteria decision-making technique (Azhar et al., 2011) usually splits the problem into small pieces. This helps the decision makers to get the clear view. These techniques mainly help in improving the quality, efficiency, rationality and explicitness of decision. It helps in reducing time and complexity. PROMETHEE (Preference Ranking Organization Method for enrichment evaluation) (Oubahman et al., 2021) involves different preference functions. It calculates the relation between alternatives for each criterion in decision making. The overall result is calculated based on net flow value. PROMETHEE (Goswami, 2020) is used in selecting the best laptop model among the six alternative laptop models based on criteria such as processor, operating system, capacity of hard disk, RAM, screen size, brand, and color. MCDM (Taherdoost et al., 2023c) helps in solving highly complex problems. There is no good or bad multi-criteria decision making method, each and every method has its advantages, and which method to use depends only upon on the problem.

Decision Support System

DSS (Mohammadi, 2018) Decision Support System supports human reasoning and helps in decision-making process. This DSS accepts the facts from the users, then processes the facts and produces the solution to the problems that are nearly same as the solutions presented by the human experts. DSS system can provide solutions to the complex decision making problems in transparent cost effective, systematic and efficient way that are not analyzed by the human experts. The concept of a decision support system (Bonczek et al., 1980) was first extracted by Peter Keen and Charles Stabell, during the late 1950s and early 1960s. Then later Bonczek (Keen et al., 1978) proposes the theory based on knowledge based DSS. In this stage he explained how the Artificial Intelligence concept was applied in DSS. Then later Mora (Mora et al., 2003) explains how the decision maker employs the computer technology in this decision making problems.

Analytic Hierarchy Process

In AHP (Kilincci et al., 2011) information is decomposed into a hierarchy of alternatives and criteria. The AHP generates a weight for each evaluation criterion according to the decision maker’s pair wise comparisons of the criteria. The higher the weight, the more important the corresponding criterion.

The procedure or steps in AHP are as follows: 1) The first step in determining the priority of an element is to make a paired comparison. 2) Then the pair wise comparison matrices represents the relative importance of an element to other elements.

Simple Additive Weighting

Based on the criteria used, it can analyze cases. This approach does not limit the use of criteria values. The concept (Stofkova et al., 2022) of aggregation is utilized by the method. The values of the criteria and weights are aggregated into a single value. The primary idea is to maximize the benefits criteria, and any problems that are minimizing can be turned into maximizing ones with the formula. The cost and benefit criteria are the minimizing and maximizing evaluation criteria in this method. This SAW method can be used in sensor selection problems, employee placement problems, stock selection problems, and ranking of best resources.

PROMETHEE II

Brans (Taherdoost, 2023b) introduced this method in 1982 and later expanded on it in 1985. The main step in this method is enriching the preference structure with several functions for preference and the dominance relations of the alternatives.

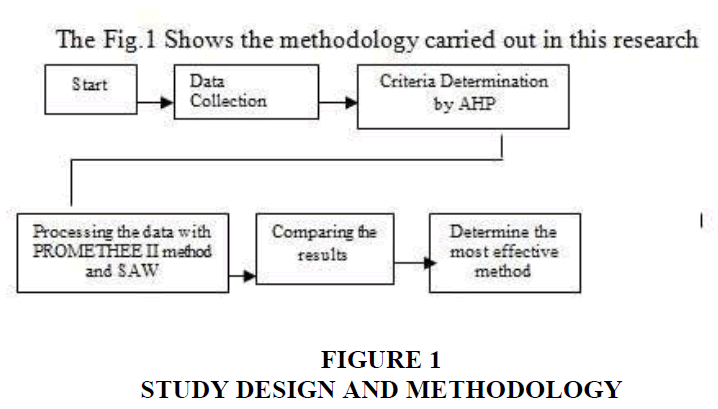
There are three stages involved in selecting the facility location problem. Finding the most appropriate distribution centers, placing them in the best possible location, and minimizing the expense of facility placement Figure 1.

PROMETHEE II Method

The steps involved in PROMETHEE II method are:

Step 1: First the decision matrix should be constructed by the decision maker for all criteria and alternatives.

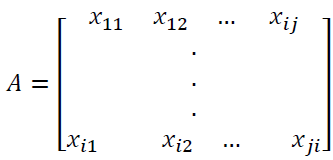
Then the normalization process for the decision matrix is done by using the below equation,

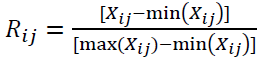
Where X_ij is the value of i^th alternative for the j^th criteria.

For cost criteria it can be rewritten as,

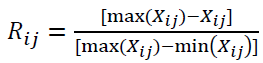
Step 2: Evaluative differences calculation of i^th alternative with respect to other alternatives.

Step 3: Preference function, 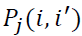calculation. There are various types of preference functions (Pelitli et al., 2020). These preference functions requiring the definition of some preferential parameters such as the preference and in differential thresholds. However, in real time applications, it is very difficult for the decision maker to specify which form of preference function is suitable for each criterion and also to determine the parameters involved. To avoid this problem, the following simplified form of preference function is used here

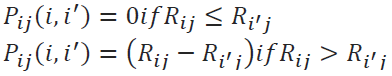
Step 4: Aggregated Preference Function calculation based on the criteria weight values.

Aggregated preference function,

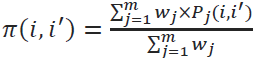
Step 5: Leaving and entering outranking flow values should be calculated. Positive (leaving) outranking flow value for i^th alternative should be calculated as,

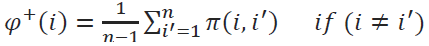
Negative (entering) outranking flow value for i^th alternative should be calculated as,

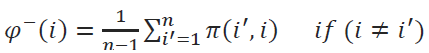
Where n is the total number of alternatives.

Each alternative has (n-1) number of other alternatives. The leaving (positive) outflow determines how much an alternative has got greater values than the other alternatives. The entering (negative) outflow determines how much an alternative is dominated by other alternatives. Complete ordering is based on the net outranking flow values in our proposed PROMETHEE II method.

Step 6: Calculation of net outranking flow values for each alternatives.

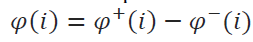
Step 7: Ranking of all the alternatives based on the value of net outranking flow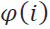. The higher the value of net outranking flow determines the best and most preferred alternative.

Simple Additive Weighting Method

The Simple Additive weighting method is one of the most common multi-attribute decision-making (MADM) methods.

Step 1. Prepare the Initial Matrix.

Step 2. Normalization is done to the value of i^th criterion for the j^th alternative. Calculating this value must be done in this step, considering whether the problem is of cost or benefit type. The difference is that in cost problems, the main objective is minimizing costs, while in benefit problems; the objective is maximizing benefits.

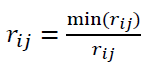, if j is a cost criteria

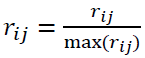, if j is benefit/profit criteria

where r_ij is the value of the i_th criterion for the j_th object. The max(r_ij) is the largest value of the i_th criterion for the j_th object. The min(r_ij) is the smallest value for it. r_ij represents the normalized value for the i_th criterion and j_th alternative.

Step 3.Integration of the values of the criteria and weights. By integrating criteria and weights, we can obtain a single value that represents the final performance value for each alternative. For this the following equation can be used for the j_th alternative.

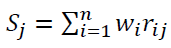
Step4. Selecting the best one is achieved by ranking alternatives. The alternative that got the highest value of S_j is selected as the best one.

Sensitivity Analysis

It (Memariani et al., 2009) shows the results of changing the weight of a single attribute on the final ranking of alternatives. Analyzing sensitivity after solving a problem can help in making precise decisions. Because the weights come from the decision maker's opinions, so the decision maker wants to determine which attribute is more sensitive than others and the extent to which a change in the weight of one criterion can impact the final results of the problem being solved. We present a novel approach for conducting sensitivity analysis on multi-attribute decision making problems. This method allows for the determination of how changes in attribute weights impact the results of a decision making problem. An analysis was conducted for the SAW and PROMETHEE II methods and the formulas are obtained.

The Effect of a Change in the Weight of one Attribute on the Weight of Other Attributes

The vector of attribute weights 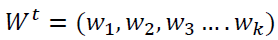where the weights are normalized and sum to 1, that is:

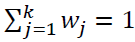
Under these assumptions, when the weight of one attribute changes, the weight of the other attributes changes accordingly, and the new vector of weights changes into

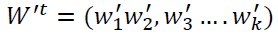
The next theorem depicts the changes in attribute weights. If the weight of P^th, attribute changes from 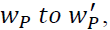in the MADM model, the weight of other attributes changes as Δj; j=1, 2,…..k.

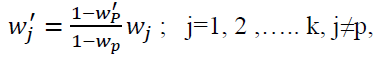
Results and Discussion

AHP in Determining Criteria Weights

AHP is a decision making tool that can be used to solve complex decision problems. It makes use of a hierarchical multi-level frame work with objectives, criteria, sub-criteria and alternatives. AHP uses pair -wise comparisons in decision making process.

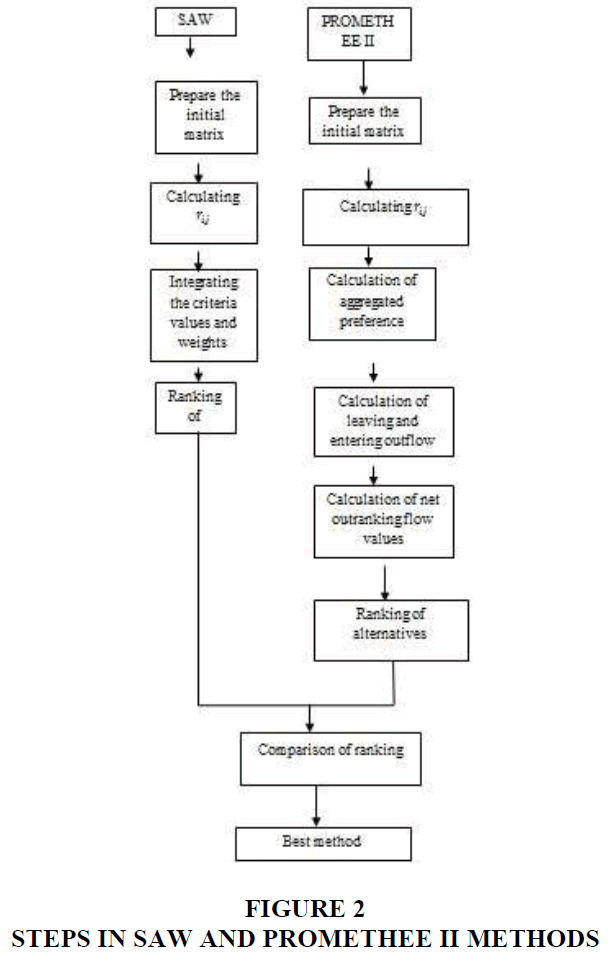
These pair wise comparisons help in determine the criteria weights and the relative performance measures of the alternatives in terms of each individual decision criterion. The steps of the SAW and PROMETHEE II method are presented in Figure 2.

The priorities will be derived from a series of measurements. Pair wise comparisons involving all the nodes. The nodes at each level will be compared, two by two, with respect to their contribution to the nodes above them.

The results of these comparisons will be entered into a matrix which is processed mathematically to derive the priorities for all the nodes on the level. Our goal is to choose the location based on four specific criteria such as Closeness to market (CM), closeness to raw material (CR), Availability of Labour (AL) and Land transportation (LT) Figure 2.

Each element of the hierarchy is given a numerical weight or priority, which makes it possible to compare elements to one another in a logical and consistent manner. Numerical priorities are determined for every alternative in the final step. These numbers allow for a clear evaluation of the different alternatives since they show how capable each alternative is of achieving the chosen course of action.

The relative weight value for each criteria are obtained by dividing the each criteria value by the sum of the of all weight value as shown.

By using the below formula we are going to get the weight value for each criteria.

Normalized score =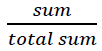

Data Preparation

In this case, the Rao used data was employed to choose the optimal facility location for a certain application using the graph theory and matrix approach (GTMA). Here, the same case is used to show how SAW and the PROMETHEE II technique are applicable and effective as MCDM tools. Four facility location selection criteria and four other facility locations are considered in this scenario.

The four selection criteria as considered here to affect the location selection decision are Closeness to market (CM), closeness to raw material (CR), Availability of Labour (AL) and Land transportation (LT) Table 1.

Table 1 AHP in Determining Criteria Weights
Demand making criteria’s/Alternatives	CM	CR	AL	LT
Medical centre1	95	165	70	100
Medical centre2	100	175	65	165
Medical centre3	90	205	85	165
Medical centre4	110	220	80	100
sum	385	765	300	525
Normalized score	0.194	0.387	0.1518	0.265

The results that can be obtained from AHP is shown in the below table. The weight values for each criterion can be calculated by using AHP method. These weight values are obtained by applying AHP and matrix of pair wise comparisons as shown in Table 2.

Table 2 Criteria Weights
Demand making criteria’s	Weight values
CM	0.194
CR	0.387
AL	0.1518
LT	0.265

Results of Promethee Ii Method

The objective and subjective information regarding different selection criteria are given in Table 3. All these criteria are expressed subjectively in linguistic terms.

Table 3 Information for Medical Centre Location Values
Location	CM	CR	LT	AT
L1	H	VH	H	AA
L2	VH	H	H	VH
L3	A	HHHH	VH	AA
L4	H	VH	A	H

The calculating steps for the PROMETHEE II method are as follows. The table 3-7 shows the results of every step. Earlier methods use complex graph theoretical approach for medical location selection problems. This methodology is time consuming and it is very complex. The same example is considered for the illustration of PROMETHEE II method. The best alternative location is selected based on eight facility location selection criteria. The value of each alternative based on the criteria are expressed in linguistic terms are given in Table 3.The values are expressed by using the 11-point scale as given in the Table 4.This 11- point scale is widely used in decision making problems. There are 4 selection criteria are considered for the selection of best medical location centre. They are nearby the emergency areas (NM), nearby blood banks (NB), low transportation cost (LT), higher patient coverage (HC).The medical centre location values based on the criteria are Closeness to market (CM), closeness to raw material (CR), Availability of Labour (AL) and Land transportation (LT)are given in the Table 3 & Table 4.

Table 4 11-Points Fuzzy Scale
Linguistic term	Crisp score
Exceptionally Low	0.045
Extremely Low	0.135
Very Low	0.255
Low	0.335
Below Average	0.410
Average	0.500
Extremely High	0.865
Exceptionally High	0.955
Above Average	0.590
High	0.665
Very High	0.745
Average	0.500

Table 5 Transformed Objective Data
Location	CM	CR	LT	AT
L1	0.665	0.745	0.665	0.590
L2	0.745	0.665	0.665	0.745
L3	0.500	0.865	0.745	0.590
L4	0.665	0.745	0.500	0.665

Table 6 Normalized Decision Matrix
Location	CM	CR	LT	AT
L1	0.6735	1	0	0
L2	1	0	0	1
L3	0	0	1	0
L4	0.6735	1	0	0

Table 7 Preference Values for all the Pairs of Medical Centre Locations
Location	CM	CR	LT	AT
(L1,L2)	0	1	0	0
(L1.L3)	0.6735	1	0	0
(L1,L4)	0	0	0	0
(L2,L1)	0.3265	0	0	1
(L2,L3)	1	0	0	1
(L2,L4)	0.3	0	0	1
(L3,L1)	0	0	1	0
(L3,L2)	0	0	1	0
(L3,L4)	0	0	1	0
(L4,L1)	0	0	0	0
(L4,L2)	0	1	0	0
(L4,L3)	0.6	1	0	0

Table 1 values are converted to crisp score by using point scale as given in Table 4. The transformed objective data is given in the Table 5.

The transformed normalized decision matrix is constructed by using the given in Table 6. Rao determined the weights of the criteria that were taken into consideration as, 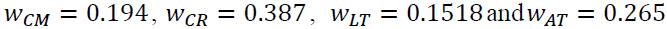using AHP method and the same criteria weights are used here for PROMETHEE II analysis Table 6.

Now the preference function is calculated for all the locations by using the results are given in the Table 7.

Table 8 provides the total aggregated preference value, which is computed for each alternative pair.

Table 8 Aggregated Preference Function
Locations	L1	L2	L3	L4
L1	-	0.387	0.518	0
L2	0.329	-	0.46	0.329
L3	0.1521	0.1521	-	0.1521
L4	0	0.387	0.518	-

The leaving and entering outflows for all the pair of alternatives are calculated and it is shown in Table 9.

Table 9 Leaving and Entering Flows Values for Different Locations
Locations	Leaving flow	Entering flow
L1	0.30166	0.160
L2	0.372	0.308
L3	0.152	0.498
L4	0.301	0.160

The net outranking flow values for the medical centre locations L1, L2.L3, L4 and L5 is calculated and shown in Table 10.

Table 10 Values of Net Outranking Flow for Different Locations
Locations	Net outranking flow values	Rank
L1	0.1413	2
L2	0.063	3
L3	-0.346	4
L4	0.143	1

The medical centre locations are prioritized as L4>L1>L2>L3.The medical centre locations are ranked based on the net outranking flow values. Thus the PROMETHEE II method is employed in solving complex decision making problems.

This methodology helps to minimize transportation cost, time, and complexity for the customers in need for emergency services. This proposed PROMETHEE II method deals with vagueness by using linguistic variables. At that point, research focus on how the vagueness are foreseen and embedded into the decision-making process. The proposed method includes a simple computation process that can be programmed easily. This demonstrates the PROMETHEE II method's applicability and potentiality for handling challenging decision-making scenarios in the manufacturing domain. The PROMETHEE II method's computational process is illustrated in the real-time industrial example provided, and it may be extended to various strategic decision-making scenarios.

Sensitivity in PROMETHEE II

If the weight of the first attribute 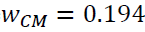is increased to 0.2, 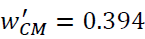the weight of other attribute changes by using as,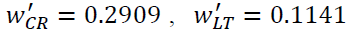 and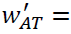 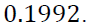Then the aggregated preference function can be obtained by using as shown in the Table 11.By using 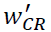can be calculated as,

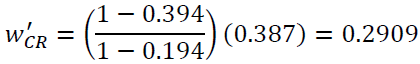
In the same way the weights of other attributes are changed based on Eq.15 and the results are shown below Table 11.

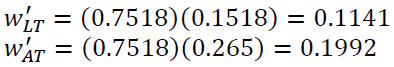
Table 11 Aggregated Preference Function
Locations	L1	L2	L3	L4
L1	-	0.29084	0.55696	0
L2	0.32859	-	0.59472	0.31812
L3	0.11443	0.11443	-	0.11443
L4	0	0.29084	0.5279	-

The leaving and entering outflows for all the pair of alternatives are calculated and it is shown in Table 12.

Table 12 Leaving and Entering Flows for Different Locations
Locations	Leaving flow	Entering flow
L1	0.2826	0.14767
L2	0.41381	0.23203
L3	0.11443	0.55986
L4	0.27291	0.14418

The net outranking flow values for the medical centre locations L1, L2.L3, L4 and L5 is calculated and shown in Table 13.

Table 13 Net Outranking Flow Values for Different Locations
Locations	Net outranking flow values	Rank
L1	0.13493	2
L2	0.18178	1
L3	-0.44543	4
L4	0.12873	3

The medical centre locations are prioritized as L2>L1>L4>L3.The medical centre locations are ranked according to the net outranking flow values. This example demonstrates that: First, changing in the weight of one attribute affects the weight of other attributes and the amount of this change is calculated. Second, the final rank of all alternatives will change after the change in the weight of the attributes. Before changing the weights of the attributes the alternatives are ranked as L4>L1>L2>L3. When the weight of one criteria is changed, it will affect the weights of other attributes and it will change the final ranking result as L2>L1>L4>L3.

Results of SAW Method

The calculating steps using the SAW are shown in the tables 14-16.After going through the calculation process, the normalized performance matrix is obtained as shown in table 14.To determine the matrix of weighted normalized decisions or matrix Y is a multiplication between the matrixes of normalized decisions (R) obtained from the Table14 with weight (W) values Table 14 & Table 15.

Table 14 Normalized Decision Matrix
Location	NM	NB	LT	AT
L1	0.6735	1	0	0
L2	1	0	0	1
L3	0	0	1	0
L4	0.6735	1	0	0

Table 15 Weighted Normalized Decision Matrix
Location	CM	CR	LT	AT
L1	0.113065	0.387	0	0
L2	0.194	0	0	0.265
L3	0	0	0.1518	0
L4	0.13065	0.387	0	0

Table 16 Saw Ranking
Location	result	Rank
L1	0.51765	1
L2	0.459	3
L3	0.1518	4
L4	0.51765	1

By using the integration of the criteria and weights to gain a single magnitude that is the final performance value for each alternative is the final value of SAW method Table 16.

The locations L1 and L4 both got the same value in the SAW method. Both are selected as best locations by using SAW method. Location L3 got the least rank.

Sensitivity in SAW

If the weight of the first attribute is increased to 0.2, 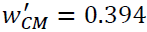the weight of other attribute changes as, 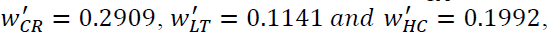then the weighted normalised matrix can be obtained by using (12) as shown in the Table 17 and the SAW method results are shown in Table 18.

Table 17 Weighted Normalized Decision Matrix
Location	CM	CR	LT	AT
L1	0.26535	0.2909	0	0
L2	0.394	0	0	0.1992
L3	0	0	0.1141	0
L4	0.26535	0.2909	0	0

Table 18 Saw Ranking
Location	result	Rank
L1	0.55625	2
L2	0.5932	1
L3	0.1141	4
L4	0.55625	2

The medical centre location L2 got the highest rank. The locations L1 and L4 got the same rank .The location L3 got the least rank based on the SAW algorithm. This example demonstrates that: First, changing in the weight of one attribute affects the weight of other attributes and the amount of this change is calculated by using. Second, the final score of all alternatives will change after the change in the weight of the attributes. Before changing the weights of the attributes the alternatives are ranked as L4>L1>L2>L3. When the weight of one criteria is changed, it will affect the weights of other attributes and it will change the final ranking result as L2>L1>L4>L3.

Comparison of the Results of PROMETHEE II and the SAW Algorithm

The final results of ranking medical centre locations by comparing the SAW method and the PROMETHEE II can be seen in the Table 19. It is depicted that the results of the ranking order are not always the same; the difference can be caused by differences in the calculation process algorithm Table 19 & Table 20.

Table 19 Comparison of the Results of the Saw and   Promethee II Algorithms
Location	SAW method	Rank	PROMETHEEII	Rank
L1	0.51765	1	0.1413	2
L2	0.459	3	0.063	3
L3	0.1518	4	-0.346	4
L4	0.51765	1	0.143	1

Table 20 Comparison of the Sensitivity Analysis of   Saw and   Promethee II Algorithms
Location	SAW method	Rank	PROMETHEEII	Rank
L1	0.55625	2	0.13493	2
L2	0.5932	1	0.18178	1
L3	0.1141	4	-0.44543	4
L4	0.55625	2	0.12873	3

From the table 19 and 20, it can be concluded that PROMETHEE II Algorithms provide the reliable and accurate results as compared to SAW method in these location selection decision making problems. SAW method does not provide the accurate results, since it provides same value and ranking for both the locations L1 and L4 as in Table 19.

Conclusion

The final results of the ranking order of locations shows different results between the SAW method and PROMETHEE II. These variations can be caused by differences in the algorithm of the calculation process. Sensitivity analysis can be applied to both SAW method and PROMETHEE II. The weight given to each criterion influences the final ranking results. Changes in weight values will also affect the final result. The results are compared and it confirms that PROMETHEE II is more effective than the SAW method in providing a good ranking. The sensitivity analysis results proved that PROMETHEE II is more robust than SAW and it provides accurate and reliable results than SAW method. Results conclude that PROMETHEE II proved to be both easy to implement and effective. Further this research work will be extended such that this PROMETHEE II Decision making techniques will be implemented in other decision support systems such as car selection, project topic selection datasets.

Acknowledgement

At the end of research, the author agreed to thank the Kalasalingam University and the accompanying lecturers who provided their assistance in carrying out the scientific research.

References

Agrawal, S., Subramanian, K. R., & Kapoor, S. (2010). Operations research-contemporary role in managerial decision making. International Journal of Research and Reviews in Applied Sciences, 3(2), 200-208..

Indexed at, Google Scholar, Cross Ref

Amiri, M., Kazemi, A., Sadaghiani, J. S., Yaghoubi, A., & Mashatzade, H. (2009). Developing and solving a new model for the location problems: Fuzzy-goal programming approach. Journal of applied sciences, 9(7), 1344-1349.

Indexed at, Google Scholar, Cross Ref

Azhar, N. A., Radzi, N. A., & Wan Ahmad, W. S. H. M. (2021). Multi-criteria decision making: a systematic review. Recent Advances in Electrical & Electronic Engineering (Formerly Recent Patents on Electrical & Electronic Engineering), 14(8), 779-801.

Indexed at, Google Scholar, Cross Ref

Bertsimas, D., & Thiele, A. (2006). Robust and data-driven optimization: modern decision making under uncertainty. In Models, methods, and applications for innovative decision making (pp. 95-122). INFORMS.

Indexed at, Google Scholar, Cross Ref

Bonczek, R. H., Holsapple, C. W., & Whinston, A. B. (1980). The evolving roles of models in decision support systems. Decision Sciences, 11(2), 337-356.

Indexed at, Google Scholar, Cross Ref

Ghose, P. S. (2021). Selection of Plant Location for a Steel Project by TOPSIS. World Journal of Applied Chemistry, 6(1), 1-5.

Indexed at, Google Scholar, Cross Ref

Goswami, S. S. (2020). Outranking methods: Promethee i and promethee ii. Foundations of Management, 12(1), 93-110.

Indexed at, Google Scholar, Cross Ref

Ishak, A., & Akmaliah, V. (2019). Analytical hierarchy process and PROMETHEE as decision making tool: a review. In IOP Conference Series: Materials Science and Engineering (Vol. 505, No. 1, p. 012085). IOP Publishing.

Indexed at, Google Scholar, Cross Ref

Keen, P. G., & Scott Morton, M. S. (1978). Decision support systems: an organizational perspective. 

Indexed at, Google Scholar

Kilincci, O., & Onal, S. A. (2011). Fuzzy AHP approach for supplier selection in a washing machine company. Expert systems with Applications, 38(8), 9656-9664.

Indexed at, Google Scholar, Cross Ref

Mani, V., Agrawal, R., & Sharma, V. (2014). Supplier selection using social sustainability: AHP based approach in India. International Strategic Management Review, 2(2), 98-112.

Indexed at, Google Scholar, Cross Ref

Memariani, A., Amini, A., & Alinezhad, A. (2009). Sensitivity analysis of simple additive weighting method (SAW): the results of change in the weight of one attribute on the final ranking of alternatives. Journal of optimization in industrial engineering, 2(4), 13-18.

Indexed at, Google Scholar

Mohammadi, M. (2018). Maria Rashidi, Maryam Ghodrat, Bijan Samali and. Manag. Inf. Syst, 19, 22.

Google Scholar

Mora M, Forgionne G, Gupta J, (2003) Decision Making Support Systems: Achievements and Challenges for the New Decade. Natural Resources Planning, Silva Fennica: Harrisburg.

Google Scholar

Önüt, S., & Soner, S. (2008). Transshipment site selection using the AHP and TOPSIS approaches under fuzzy environment. Waste management, 28(9), 1552-1559.

Indexed at, Google Scholar, Cross Ref

Oubahman, L., & Duleba, S. (2021). Review of PROMETHEE method in transportation. Production Engineering Archives, 27(1), 69-74.

Indexed at, Google Scholar, Cross Ref

Pelitli, T., Karagöz, E., & Yaralioğlu, K. (2020). The Determination of Food Preferences with PROMETHEE Multi-criteria Decision-Making Method: A Web-Based Application. In Economic and Financial Challenges for Balkan and Eastern European Countries: Proceedings of the 10th International Conference on the Economies of the Balkan and Eastern European Countries in the Changing World (EBEEC) in Warsaw, Poland 2018 (pp. 329-341). Springer International Publishing.

Indexed at, Google Scholar, Cross Ref

Siahaan, M. D. L., Elviwani, A. B. S., Lubis, A. H., & Siahaan, A. P. U. (2017). Implementation of simple additive weighting algorithm in particular instance. International Journal of Scientific Research in Science and Technology, 3(6), 442-447.

Indexed at, Google Scholar, Cross Ref

Stofkova, J., Krejnus, M., Stofkova, K. R., Malega, P., & Binasova, V. (2022). Use of the analytic hierarchy process and selected methods in the managerial decision-making process in the context of sustainable development. Sustainability, 14(18), 11546.

Indexed at, Google Scholar, Cross Ref

Taherdoost, H. (2023). Analysis of Simple Additive Weighting Method (SAW) as a Multi-Attribute Decision-Making Technique: A Step-by-Step. Taherdoost, H, 21-24.

Indexed at, Google Scholar, Cross Ref

Taherdoost, H., & Madanchian, M. (2023). Multi-criteria decision making (MCDM) methods and concepts. Encyclopedia, 3(1), 77-87.

Indexed at, Google Scholar, Cross Ref

Taherdoost, H., & Madanchian, M. (2023). Using PROMETHEE method for multi-criteria decision making: Applications and procedures. Iris Journal of Economics & Business Management, 1(1).

Indexed at, Google Scholar, Cross Ref

Yong, D. (2006). Plant location selection based on fuzzy TOPSIS. The International Journal of Advanced Manufacturing Technology, 28, 839-844.

Indexed at, Google Scholar, Cross Ref

Received: 03-Apr-2024 Manuscript No. JMIDS-24-15163; Editor assigned: 04-Apr-2024 Pre QC No. JMIDS-24-15163(PQ); Reviewed: 15-Apr-2024 QC No. JMIDS-24-15163; Revised: 22-Apr-2024 Manuscript No. JMIDS-24-15163(R); Published: 30-Apr-2024