Research Article: 2019 Vol: 23 Issue: 4
The Impact of Product Market Competition on Debt Ratio in Vietnam Stock Market
Tan Vinh Nguyen, Academy of Politics Region
Thi Oanh Nguyen, Academy of Politics Region
Abstract
Asymmetric information has caused difficulties for investors in the financial market when the enterprises have high competitiveness in the market but there are acts of using unusual debt ratio. Investment decisions on the stock market of investors will be negatively affected by asymmetric information. Therefore, the authors conduct research to assess the impact of product market competition on the debt ratio of enterprises listed in the Vietnam stock market (excluded the enterprises operating in the financial field) from 2010 to 2018. By analyzing panel data through the Difference Generalized method of moment (D-GMM), the research results indicate: Competitiveness factors (Tobin's Q and HHI) have a negative impact on debt ratio (DR)- the results support the predation theory. When businesses are highly competitive, there will be a tendency to reduce the debt ratio. From the results of this research, good signals of enterprises in the market (Tobin’s Q high) will reduce external debt. Besides, if these companies issue more shares, it is also a good signal for investors (according to the pecking order theory) because capital is not an urgent issue for businesses at this time when they are high competition in the market. At the same time, low-competitive enterprises will be threatened when the debt ratio tends to increase, making pressure on loan payments increase. HHI competition index (Herfindahl-Hirschman Index) has the opposite effect on debt ratio of large-scale enterprises. It can be seen that large-scale enterprises, with high economic potential when highly competitive, create pressure on enterprises with low competition, enterprises tend to reduce debt ratio. At the same time, low-competitive enterprises cannot increase their capital by issuing shares because this reduces the value of the business according to information asymmetry theory.
Keywords
Product Market Competition, Capital Structure, GMM Model
Introduction
In the business environment, firms are always faced with policies on capital needs to expand or maintain business (Moeinaddin et al., 2013). For businesses with low competitiveness, increasing debt leads to a risk of bankruptcy that will force businesses to reduce their debt ratio to limit the amount of payments each period (Scott, 1976). Therefore, firms in different situations have different debt ratio strategies, and each strategy using debt ratio can affect competitors' behavior in the market (Guney et al., 2011). This strategy will change the competitive position in the market. Therefore, researchers have proposed three basic modeling methods to explain the relationship between product market competition and debt ratio: (1) Limited ability; (2) predation model; (3) investment effect model (Guney et al., 2011; Moeinaddin et al., 2013).
With the predation model, a high-leverage company is threatened by companies with lower financial leverage (Bolton & Scharfstein, 1990; Brander & Lewis, 1986; Opler & Titman, 1994). The model specifies that investors who enter new markets will be more vulnerable than incumbents. Companies with high financial leverage will significantly lose more market share than companies with low financial leverage in the recession industry (Guney et al., 2011; Opler & Titman, 1994). Incumbents having deep pocket are willing to come up with price and output policies to create great pressure on new market participants. These actions will increase their market shares and new entrants may have to withdraw from the market without large financial potentials (Gui-Diby, 2016; Guney et al., 2011). Since then, the company will have a policy to encourage debt reduction. These arguments indicate the negative relationship between product market competition and debt ratio.
In limited liability model, there have been shown a clear relationship between debt ratio and product market competition. Good firm performance helps to increase competition in the market, leading to creditors willing to lend more because they are not afraid of debt recovery. In contrast, when businesses are not performing well, the competitiveness in the market is low, making creditors afraid of debt recovery, thus limiting loan sources as well as creating restrictions in loan contracts.
With investment effect model, debt is the cause of under-investment due to the asset substitution effect (Myers, 1984; Phillips, 1995). Increase in debt will be a signal for investors not to invest in the future due to increased cash costs in each period (Guney et al., 2011). Therefore, the benefits or profits of shareholders will be partially shared to lenders because internal finance is always cheaper than external sources such as debt or equity. Therefore, according to information asymmetry theory, the increase in equity through issuing shares or debt is also a signal that the competitiveness of the company decreases.
Among previous studies, some have shown a negative relationship between leverage and product market competition (Barclay, Smith, & Watts, 1995; Titman & Wessels, 1988), some have found a positive relationship between debt ratio and product market competition (Fosu, 2013; Guney et al., 2011; Michaelas, Chittenden, & Poutziouris, 1999). In the research context of Vietnam, the author has not found adequate research on the relationship between debt ratio and product market competition, considering both the market and the industry and the comparison of a competitive company (high and low competition). Therefore, the author selected the topic "Impact of product market competition on debt ratio in Vietnam stock market".
Literature Review
Debt ratio is a financial term that describes the origin and method of forming firms’ capital to buy assets, material means and maintain business activities. Debt ratio takes an important role in utilizing firms’ activities because it concerns the decisions of combining different sources of capital (Khan, 2012). These sources include long-term debts, short-term debts (known as debts), preferred stocks and common stocks (also known as capital stock). Setting up an optimal debt ratio will lead to effective financial performance, as well as, increase firms’ competitiveness (Terra, 2008).
Competitiveness of enterprises is the ability to maintain and expand the market share of enterprises. National competitiveness is the ability of a country to achieve a high and sustainable per capita income ratio (Krugman, 1994; Porter, 1997). The competitiveness of one industry is measured by concentration or scatter ratio of its market share (Moeinaddin et al., 2013). The more scattering its market share is, the more competitive the industry is and vice versa. They discussed about HHI index which is usually used to evaluate the competitiveness of firms or industries. According to the, HHI is a strong index to assess the competitive capabilities by sectors and ranges from 0 to 1. The greater the index is, the more the market share concentrates on some particular enterprises, which means the less competitive the market becomes (Moeinaddin et al., 2013).
Guney et al (2011) have conducted their research in Chinese market and pointed out that: there was a linear, as well as, nonlinear relationship between factors of competition HHI and debt ratio of firms. Sumitra & Malabika (20) have studied and found the influence of competition in product market which some firms have to face in such a developing country as India on decisions of debt ratio firms have to make (Naha & Roy, 2011).
Research Design
Research Model
The dependent variable is the debt ratio and is defined as the ratio of total debt to total assets. The independent variable is product market competition in my thesis. Product market competition can be measured by Tobin’s Q or Herfindahl-Hirschman Index (HHI). These variables are theoretically sound and reliable indicators of a firm’s market power (Boghean & State, 2015; Fosu, 2013; Lindenberg & Ross, 1981). In addition, the research also adds model also incorporates control variables that may affect debt ratio.
Model 1: Impact of Tobin’s Q on Debt ratio
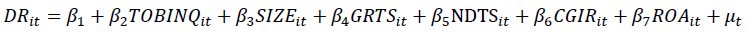
Model 2: Impact of HHI on Debt ratio
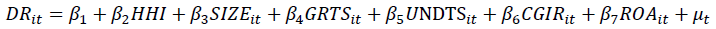
Definition of Variables and the Relationship between Capital and Independent Variables
Debt ratio: is dependent variable in the research model and is calculated based on total liabilities/total assets. At the same time, the independent variable is the competition of the enterprise measured by the criteria of Tobin’s Q and Herfindahl–Hirschman Index (HHI) based on the strength of the enterprise in the market (Guney et al., 2011; Lindenberg & Ross, 1981). Tobin’s Q is the difference between the market value and the book value of the enterprise.
Profitability: is a characteristic quantity for profitability on assets of ROA enterprises is an important quantity indicating how profitable a company is. This research variable was measured by return on assets (ROA), which is calculated by operating profit divided by total assets. Higher profitability creates larger retained earnings; as a results, businesses can reduce debt ratio to reduce the cost of interest. However, businesses can also continue to increase debt ratio to control agency costs in enterprises (Guney et al., 2011; Jensen, 1986).
Firm Size: The size of the enterprise represents how large total assets or total capital of the enterprise are. Size is measured by taking the loga nepe of total assets. Large businesses will tend to diversify the portfolio to limit financial risks, and this diversification makes the debt ratio of firm increase.
Growth rate: is measured by annual growth of revenue. Enterprises with high revenue growth will be able to generate large cash flows. Therefore, the ability to use debt ratio of companies will also decrease.
Non-debt tax shield: are items such as depreciation or pension funds used in the enterprise for the purpose of reducing corporate tax payable. Businesses that use more non-debt tax shield tend to use less debt (Guney et al., 2011). Non-debt tax shield in this study is measured by the depreciation rate on total assets.
Capability of generating internal resources: when firms have good internal capital resources, it is preferable to use these resources before raising capital according to the classification order theory. Besides, in order to make good use of the tax shield through the use of financial leverage, businesses still want to use loan capital with tax advantages (Jensen, 1986). Therefore, capability of generating internal resources can have positive or negative impact on firm debt ratio.
The research variables are detailed in Table 1.
| Table 1 Definition of Variables | ||
| Variables | Symbol | De?nition |
| Dependent variable: Debt ratio |
DR | Debt ratio=total liabilities/total assets |
| Independent variables: | ||
| Tobin's Q | TobinsQ | Book value of total liabilities plus market value of total shares/book value of total assets |
| HHI | HHI | HHIi= (xj/∑xj)2 xj is revenue of firm j |
| Control variables | ||
| Pro?tability | ROA | Operating pro?t/total assets |
| Firm size | SIZE | Ln (total assets) |
| Growth rate | GRTS | (Total salest − total salest-1) /total salest-1 |
| Non-debt tax shield | NDTS | Depreciation/total assets |
| Capability of generating internal resources | CGIR | Net cash ?ow of operations/total assets |
Data
Secondary database is collected from audited financial statements of enterprises (only Non-financial Company) from 2010 to 2018 through FiinPro data system provided by StoxPlus Corporation (balanced panel data). The variables are calculated before inputting data analysis with STATA software.
After preparing data, the author proceeds to describe the enterprises’ characteristics according to the business value and the size of the business. While low-value companies (Tobin’s Q smaller than 1) have an average debt ratio of 0.52, this variable is lower (0.31) for high value companies. The competition index measured by HHI for low-value group is 0.18% smaller than the high value (0.31%). The average of ROA of low-value group is also smaller than that of high value companies. However, revenue growth of the former is higher than that of the latter. Non-debt tax shield on the generation and security of internal resources of low-value businesses are higher than that of high-value businesses. Details of variables are described in the Table 2.
| Table 2 Descriptive Variables by Firm Value | ||||||
| Variable | Obs | Mean | Std. Dev. | Min | Max | |
| Low value | DR | 4,887 | 0.525983 | 0.216807 | 0.000471 | 0.983578 |
| TobinsQ | 4,887 | 0.364844 | 0.257168 | 0 | 0.999793 | |
| HHI | 4,885 | 0.183248 | 2.569292 | 0 | 62.72393 | |
| ROA | 4,885 | 0.045207 | 0.070824 | -1.75887 | 0.783739 | |
| ASSET | 4,887 | 1.78E+12 | 4.39E+12 | 6.10E+09 | 7.82E+13 | |
| GRTS | 4,326 | 0.362349 | 11.98194 | -0.87553 | 783.2474 | |
| NDTS | 4,887 | -0.1975 | 0.245403 | -1.83709 | 0 | |
| CGIR | 4,850 | 0.038723 | 0.154039 | -2.59208 | 2.018969 | |
| High value | DR | 861 | 0.319231 | 0.176998 | 0.009166 | 0.896111 |
| TobinsQ | 861 | 1.880057 | 1.100546 | 1.000575 | 9.759737 | |
| HHI | 861 | 0.132533 | 7.615592 | 0 | 78.98392 | |
| ROA | 860 | 0.124484 | 0.116214 | -0.8965 | 0.716832 | |
| ASSET | 861 | 4.29E+12 | 1.78E+13 | 9.97E+08 | 2.89E+14 | |
| GRTS | 759 | 0.166409 | 0.880752 | -0.61017 | 19.33624 | |
| NDTS | 861 | -0.2984 | 0.311326 | -1.89122 | 0 | |
| CGIR | 852 | 0.122619 | 0.148208 | -0.60581 | 0.733143 | |
Described by firm size, it indicates that the larger the scale of enterprises, the higher the debt utilization rate. Small companies have a higher value, or Tobin’s Q than medium and large companies. In contrast, the companies with high competition HHI are small and medium enterprises. High revenue growth belongs to larger enterprises. Non-debt tax shield of small business is lower than that of medium and large enterprises. The value of capability of generating internal resources is almost no different between businesses of different sizes. Details of the variables described in Table 3.
| Table 3 Descriptive Variables by Size | ||||||
| Variable | Obs | Mean | Std. Dev. | Min | Max | |
| Small | DR | 55 | 0.262673 | 0.194618 | 0.000471 | 0.862891 |
| TobinsQ | 55 | 1.11794 | 1.112306 | 0.011428 | 5.045582 | |
| HHI | 55 | 3.31E-05 | 7.92E-05 | 0 | 0.000466 | |
| ROA | 55 | 0.042439 | 0.078697 | -0.25206 | 0.222692 | |
| ASSET | 55 | 1.53E+10 | 4.01E+09 | 9.97E+08 | 1.99E+10 | |
| GRTS | 40 | -5.3E-05 | 0.155161 | -0.30698 | 0.734948 | |
| NDTS | 55 | -0.14455 | 0.183866 | -1.13863 | 0 | |
| CGIR | 55 | 0.04466 | 0.158893 | -0.54852 | 0.527061 | |
| Medium | DR | 598 | 0.370904 | 0.200634 | 0.008356 | 0.959671 |
| TobinsQ | 598 | 0.713276 | 0.661511 | 0 | 4.627197 | |
| HHI | 596 | 0.000131 | 0.000396 | 0 | 0.004173 | |
| ROA | 596 | 0.053513 | 0.082559 | -0.47157 | 0.394106 | |
| ASSET | 598 | 5.77E+10 | 2.26E+10 | 2.00E+10 | 1.00E+11 | |
| GRTS | 494 | 0.116476 | 0.665631 | -0.43818 | 8.326454 | |
| NDTS | 598 | -0.25942 | 0.294206 | -1.89122 | 0 | |
| CGIR | 589 | 0.047402 | 0.152554 | -0.90688 | 0.608482 | |
| Large | DR | 5,095 | 0.512088 | 0.220717 | 0.001981 | 0.983578 |
| TobinsQ | 5,095 | 0.571874 | 0.72686 | 0 | 9.759737 | |
| HHI | 5,095 | 0.399647 | 4.036077 | 0 | 78.98392 | |
| ROA | 5,094 | 0.057649 | 0.084406 | -1.75887 | 0.783739 | |
| ASSET | 5,095 | 2.42E+12 | 8.48E+12 | 1.00E+11 | 2.89E+14 | |
| GRTS | 4,551 | 0.359545 | 11.68534 | -0.87553 | 783.2474 | |
| NDTS | 5,095 | -0.20785 | 0.254475 | -1.88118 | 0 | |
| CGIR | 5,058 | 0.05178 | 0.156458 | -2.59208 | 2.018969 | |
Methods of Data Analysis
With analytical data characteristics for companies listed from 2010 to 2018, the panel data model will be used for analysis. The data, after had been collected, were input to the STATA software for analysis. Basic models, such as fixed effect and Random effect were put in priority. Hausman test is used to evaluate the appropriateness for the real research data between Fixed effect and Random effect (Hausman, 1978).
In case there are some problems with the model, such as autocorrelation, heteroscedasticity, endogeneity, we will use the Difference GMM (Difference Generalized method of moments) of Arellano - Bond (1991) to fix them. The method of Arellano - Bond is designed to correct the fixed effects implied in the error term of the model due to some unchanged characteristics by time of the studied firms; for example, location and types of business can correlate with explanatory variables in the model. This test is so used for panel data with a short period of time (time = 9 years) and a large number of companies because it can make a shock firms’ fixed effects, which are reflected in the error term, reduced by time.
Sargan test (Hansen test) and Arellano - Bond test will be used to test the appropriateness of the estimation results of GMM. Sargan test determines the appropriateness of instrumental variables in GMM model. This is a test for over - identification restrictions, of which null hypothesis is that instrumental variables are exogenous. Arellano - Bond test, is used to test for autocorrelation of variance in GMM model in first differenced-errors. Therefore, the difference series studied implicitly have linear correlation - AR(1), the testing results are ignored Autocorrelation test- AR(2) is tested on the difference series of error terms to detect autocorrelation of error terms at quadratic. Hypothesis H0 of Arellano-Bond test does not have autocorrelation and is applied for the remainder of differences.
Results
Results of regression analysis with FEM and REM models are both displayed in the Table 4. However, endogenous problem often occurs in these models. To solve those problems and make the model more stable, the authors also use the GMM model to analyze the results.
| Table 4 Regression Results by Firm Value | ||||||
| Low value | High value | |||||
| VARIABLES | FEM | REM | GMM | FEM | REM | GMM |
| TobinsQ | -0.578*** | -0.493*** | -0.206*** | -0.0485*** | -0.0402*** | -0.0278*** |
| (0.0142) | (0.0128) | (0.0428) | (0.00654) | (0.00574) | (0.00980) | |
| ROA | -0.389*** | -0.363*** | 0.0355 | -0.479*** | -0.449*** | -0.0381 |
| (0.0211) | (0.0215) | (0.0327) | (0.0465) | (0.0434) | (0.0507) | |
| SIZE | -0.0103*** | 0.0103*** | 0.0615*** | 0.0157*** | 0.0240*** | 0.0230** |
| (0.00314) | (0.00274) | (0.0160) | (0.00544) | (0.00440) | (0.00956) | |
| NDTS | 0.186*** | 0.153*** | 0.526*** | 0.211*** | 0.171*** | 0.268*** |
| (0.0143) | (0.0133) | (0.0774) | (0.0278) | (0.0230) | (0.0548) | |
| CGIR | -0.000829 | 0.00256 | 0.160*** | -0.0565** | -0.0564** | 0.106** |
| (0.00866) | (0.00890) | (0.0401) | (0.0245) | (0.0242) | (0.0498) | |
| Constant | 1.077*** | 0.491*** | -0.917** | 0.123 | -0.138 | -0.241 |
| (0.0865) | (0.0757) | (0.444) | (0.151) | (0.122) | (0.256) | |
| Observations | 4,301 | 4,301 | 3,813 | 810 | 810 | 716 |
| R-squared | 0.412 | 0.322 | ||||
| Number of id | 546 | 546 | 546 | 155 | 155 | 151 |
| AR(2) | 0.380 | 0.532 | ||||
| Hansen test | 0.215 | 0.343 | ||||
Analyze the Impact of Tobin’s Q, HHI on Debt Ratio by Firm Value
The model results for high value and low value enterprises all have similar results: The Tobin’s Q has a negative impact on debt ratio. Firm size, capability of generating internal resources and non-debt tax shield has positive impacts on the debt ratio of enterprises. ROA does not affect the debt ratio of the companies (Tables 5-7).
| Table 5 Regression Results by Firm Value | ||||||
| Low value | High value | |||||
| VARIABLES | FEM | REM | GMM | FEM | REM | GMM |
| HHI | 0.00357* | 0.00253 | -0.000482*** | 6.59e-05 | 0.00115 | -0.00168*** |
| (0.00200) | (0.00167) | (5.23e-05) | (0.00282) | (0.00167) | (2.90e-05) | |
| ROA | -0.373*** | -0.388*** | -0.371*** | -0.463*** | -0.449*** | -0.196*** |
| (0.0253) | (0.0253) | (0.0457) | (0.0484) | (0.0448) | (0.0119) | |
| SIZE | 0.0227*** | 0.0341*** | 0.0105*** | 0.0307*** | 0.0311*** | 0.0280*** |
| (0.00364) | (0.00303) | (0.000865) | (0.00529) | (0.00447) | (0.00110) | |
| NDTS | 0.323*** | 0.248*** | 0.262*** | 0.226*** | 0.173*** | 0.184*** |
| (0.0167) | (0.0149) | (0.0297) | (0.0288) | (0.0235) | (0.00530) | |
| CGIR | -0.0141 | -0.0164 | -0.392*** | -0.0592** | -0.0602** | -0.0589*** |
| (0.0104) | (0.0105) | (0.0156) | (0.0256) | (0.0250) | (0.00305) | |
| Constant | 0.00586 | -0.324*** | -0.0405 | -0.370*** | -0.395*** | -0.590*** |
| (0.0989) | (0.0825) | (0.0280) | (0.142) | (0.121) | (0.0343) | |
| Observations | 4,301 | 4,301 | 3,813 | 810 | 810 | 716 |
| R-squared | 0.152 | 0.264 | ||||
| Number of id | 546 | 546 | 546 | 155 | 155 | 155 |
| AR(2) | 0.214 | 0.924 | ||||
| Hansen test | 0.278 | 0.148 | ||||
| Table 6 Regression Results by Firm Size | |||||||||
| Small | Medium | Large | |||||||
| VARIABLES | FEM | REM | GMM | FEM | REM | GMM | FEM | REM | GMM |
| TobinsQ | -0.175** | -0.116*** | -0.0336* | -0.252*** | -0.142*** | -0.0375** | -0.143*** | -0.126*** | -0.0697*** |
| (0.0741) | (0.0440) | (0.0182) | (0.0292) | (0.0192) | (0.0147) | (0.00630) | (0.00535) | (0.0138) | |
| ROA | 0.0511 | 0.00173 | 0.149 | -0.367*** | -0.284*** | 0.0252 | -0.388*** | -0.385*** | -0.0633** |
| (0.113) | (0.0973) | (0.361) | (0.0637) | (0.0622) | (0.0309) | (0.0212) | (0.0211) | (0.0300) | |
| SIZE | 0.0425 | 0.0213 | 0.00289 | 0.0487** | 0.0855*** | 0.00278 | 0.0292*** | 0.0375*** | 0.0311*** |
| (0.0791) | (0.0620) | (0.208) | (0.0202) | (0.0179) | (0.0379) | (0.00342) | (0.00297) | (0.0102) | |
| NDTS | 0.00649 | 0.237 | 0.0833 | 0.123*** | 0.100*** | 0.0545 | 0.281*** | 0.235*** | 0.418*** |
| (0.367) | (0.195) | (0.0907) | (0.0396) | (0.0353) | (0.0434) | (0.0138) | (0.0127) | (0.0646) | |
| CGIR | 0.118* | 0.118** | 0.0228 | -0.119*** | -0.120*** | -0.215*** | -0.00330 | -0.00187 | 0.0351 |
| (0.0583) | (0.0533) | (0.0839) | (0.0301) | (0.0301) | (0.0346) | (0.00913) | (0.00920) | (0.0365) | |
| Constant | -0.517 | 0.00246 | 0.118 | -0.595 | -1.583*** | 0.263 | -0.111 | -0.364*** | -0.231 |
| (1.903) | (1.457) | (4.858) | (0.509) | (0.447) | (0.941) | (0.0947) | (0.0819) | (0.275) | |
| Observations | 51 | 51 | 39 | 582 | 582 | 487 | 4,478 | 4,478 | 4,003 |
| R-squared | 0.347 | 0.313 | 0.309 | ||||||
| Number of id | 18 | 18 | 18 | 112 | 112 | 112 | 546 | 546 | 546 |
| AR(2) | 0.534 | 0.800 | 0.538 | ||||||
| Hansen test | 0.825 | 0.368 | 0.127 | ||||||
| Table 7 Regression Results by Firm Size | |||||||||
| Small | Medium | Large | |||||||
| VARIABLES | FEM | REM | GMM | FEM | REM | GMM | FEM | REM | GMM |
| HHI | 78.74 | 137.1 | 3.370 | 27.86 | 30.06 | 55.59** | 0.00154 | 0.000128 | -0.000498*** |
| (273.3) | (239.2) | (86.69) | (23.01) | (19.29) | (27.84) | (0.00158) | (0.00122) | (9.29e-05) | |
| ROA | 0.0502 | 0.00406 | -0.129 | -0.240*** | -0.243*** | -0.158 | -0.390*** | -0.420*** | -0.285*** |
| (0.123) | (0.105) | (0.0766) | (0.0667) | (0.0652) | (0.113) | (0.0225) | (0.0224) | (0.0360) | |
| SIZE | 0.112 | 0.0853 | -0.0833 | 0.114*** | 0.115*** | -0.0303 | 0.0470*** | 0.0477*** | 0.0172*** |
| (0.0809) | (0.0611) | (0.0676) | (0.0201) | (0.0182) | (0.0624) | (0.00355) | (0.00313) | (0.00155) | |
| NDTS | 0.00377 | 0.207 | -0.0241 | 0.185*** | 0.145*** | -0.118 | 0.327*** | 0.275*** | 0.236*** |
| (0.417) | (0.211) | (0.0559) | (0.0419) | (0.0361) | (0.0814) | (0.0145) | (0.0134) | (0.0137) | |
| CGIR | 0.155** | 0.145** | -0.0130 | -0.165*** | -0.151*** | -0.412*** | -0.000877 | -0.00563 | -0.332*** |
| (0.0617) | (0.0567) | (0.0530) | (0.0319) | (0.0314) | (0.123) | (0.00971) | (0.00981) | (0.0210) | |
| Constant | -2.361 | -1.608 | 1.976 | -2.390*** | -2.405*** | 0.765 | -0.669*** | -0.703*** | -0.177*** |
| (1.908) | (1.413) | (1.586) | (0.499) | (0.452) | (1.554) | (0.0973) | (0.0858) | (0.0452) | |
| Observations | 51 | 51 | 39 | 582 | 582 | 487 | 4,478 | 4,478 | 4,003 |
| Number of id | 18 | 18 | 18 | 112 | 112 | 112 | 546 | 546 | 546 |
| AR(2) | 0.539 | 0.240 | |||||||
| Hansen test | 0.813 | 0.117 | |||||||
HHI has a negative impact on debt ratio for both high value and low-value businesses in the market, similar to the effects of Tobin’s Q (HHI and Tobin’s Q have negative effects on debt ratio). The two factors SIZE and NDTS both have positive impacts on debt ratio, while the impact of CGIR on debt ratio is negative. It is noticeable that the impact of HHI as explainatory variable making the relationship between CGIR and debt ratio turn into opposite direction. The results also show that ROA has the negative effect on debt ratio.
Analyze The Impact of Tobin’s Q, HHI on Debt Ratio by Firm Size
The results show that for companies of different sizes, the debt ratio is negatively impacted by Tobin's Q. Besides, ROA only has negative effects on debt ratio of large enterprises and these effects are insignificant for small and medium-sized businesses. The SIZE factor does not affect the small and medium enterprises’ debt ratio but has a positive impact on debt ratio of large enterprises. Similarly, NDTS affects the debt ratio of large enterprises in positive way and does not affect debt ratio of small and medium enterprises. Finally, CGIR only adversely affect debt ratio for medium enterprises but does not affect the debt ratio of small businesses and large enterprises.
For medium enterprises, HHI has a positive impact, but for large enterprises HHI has the opposite effect. While ROA has a negative impact on the debt ratio of small and large enterprises, ROA does not affect the debt ratio of medium enterprises. SIZE and NDTS only affect debt ratio in large enterprises and do not affect the debt ratio of small and medium enterprises. CGIR does not affect the debt ratio of small businesses but has a negative impact on the debt ratio of medium and large enterprises.
Discussion
The Tobin’s Q has a negative impact on debt ratio, which indicates that firms with good information on the market (market value is higher) tend to reduce the debt ratio. This result is similar to the previous studies of Barclay, Smith, & Watts (1995); Titman & Wessels, (1988). This result also supports the theory of predation suggesting when businesses are highly appreciated by investors in the market they will have an advantage over businesses with low market value. Lower Tobin’s Q value businesses tend to borrow more capital for their operations instead of using internal capital sources or issuing additional shares. Asymmetric information significantly affects the debt ratio of businesses. The asymetric information theory suggests that raising capital from issuing shares may send bad signals to the market about the shortage of capital. This has caused businesses’s Tobin’s Q to devalue and they tend to switch to using loans to avoid continued decline. In contrast to businesses with increased value of Tobin’s Q, the level of investor interest also increases. This may be due to good business results leading to much more capital used from retained earnings.
HHI has a negative impact on debt ratio of enterprises. It can be seen that enterprises with high economic potential and high competition will put pressure on enterprises with low competition by reducing debt ratio. It can be seen that businesses are not risking a trade-off between high competition and high debt ratio (not risking in using leverage). In addition, companies with reduced competitiveness tend to borrow more debts (not to use equity) to ensure the value of enterprises in the market. The fact that low-competitive companies borrow more debt will be subject to further pressure on cost of debt and from businesses with great competitiveness while taking advantage of products to put pressure on competitive enterprises low.
ROA does not affect debt ratio of small and medium enterprises (SMEs) but has a negative effect on debt ratio of large enterprises. It can be seen that the large companies apply the tax shield more effectively than SMEs. ROA of large enterprises is statistically larger than the ROA of SMEs. Therefore, the use of financial leverage in SMEs seems to be inefficient compared to large enterprises. The large company is more efficient businesses as it has brought in greater internal capital (retained earnings). It will help large enterprises be more flexible in selecting investment capital (there are more options when there is an excess of internal capital). In contrast to SMEs with lower ROA, the decision to use capital depends heavily on capital outside the enterprises.
The SIZE factor only has a positive impact on the debt ratio of large enterprises without affecting the debt ratio of SMEs in both low and high enterprise value. Expanding firm size for large enterprises is positively associated with external loans; the companies often use internal capital. The pressure of enterprise with interest expenses when using too much external loans. For SMEs, expanding size does not relate to debt ratio; this result shows that SMEs still tend to use external loans when internal resources are limited.
Non-debt tax shield (NDTS) also only affects the debt ratio of large enterprises without affecting the debt ratio of SMEs. For large enterprises, large depreciated assets lead to the use of NDTS to bring efficiency for effective application of tax incentives for companies. Application of NDTS will make policies using tax shields more diversified and make the use of debt ratio also be reduced as large enterprises are able to diversify preferential policies to tax. SMEs are more disadvantaged with NDTS when the use of NDTS is not effective in optimizing the tax incentives of enterprises.
References
- Arellano, M., & Bond, S. (1991). Some tests of specification for panel data: Monte carlo evidence and an application to employment equations. The Review of Economic Studies, 58(2), 277-297.
- Barclay, M.J., Smith, C.W., & Watts, R.L. (1995). The determinants of corporate leverage and dividend policies. Journal of Applied Corporate Finance, 7(4), 4-19.
- Boghean, C., & State, M. (2015). The relation between foreign direct investments (FDI) and labour productivity in the european union countries. Procedia Economics and Finance, 32, 278-285.
- Bolton, P., & Scharfstein, D.S. (1990). A theory of predation based on agency problems in financial contracting. The American Economic Review, 80(1), 93-106.
- Brander, J.A., & Lewis, T.R. (1986). Oligopoly and financial structure: The limited liability effect. The American Economic Review, 76(5), 956-970.
- Fosu, S. (2013). Capital structure, product market competition and firm performance: Evidence from South Africa. The Quarterly Review of Economics and Finance, 53(2), 140-151.
- Gui-Diby, S.L. (2016). Impact of foreign direct investments on economic growth in Africa: Evidence from three decades of panel data analyses. Research in Economics, 68(3), 248-256.
- Guney, Y., Li, L., & Fairchild, R. (2011). The relationship between product market competition and capital structure in Chinese listed firms. International Review of Financial Analysis, 20(1), 41-51.
- Hausman, J.A. (1978). Specification tests in econometrics. Econometrica, 46(6), 1251-1271.
- Jensen, M.C. (1986). Agency costs of free cash flow, corporate finance, and takeovers. The American Economic Review, 76(2), 323-329.
- Krugman, P. (1994). Competitiveness: A dangerous obsession. Foreign Affairs, 73, 28.
- Lindenberg, E.B., & Ross, S.A. (1981). Tobin’s q ratio and industrial organization. The Journal of Business, 54(1), 1–32.
- Michaelas, N., Chittenden, F., & Poutziouris, P. (1999). Financial policy and capital structure choice in U.K. SMEs: Empirical evidence from company panel data. Small Business Economics, 12(2), 113-130.
- Moeinaddin, M., Nayebzadeh, S., & Ghasemi, M. (2013). The relationship between product market competition and capital structure of the selected industries of the tehran stock exchange. International Journal of Academic Research in Accounting, Finance and Management Sciences, 3(3), 221-233.
- Myers, S.C. (1984). Capital Structure Puzzle, (Working Paper No. 1393).
- Naha, S., & Roy, M. (2011). Product market competition and capital structure of firms: The indian evidence. Journal of Quantitative Economics, 9, 140-153.
- Opler, T.C., & Titman, S. (1994). Financial distress and corporate performance. The Journal of Finance, 49(3), 1015-1040.
- Phillips, G.M. (1995). Increased debt and industry product markets an empirical analysis. Journal of Financial Economics, 37(2), 189-238.
- Porter, M.E. (1997). Competitive strategy. Measuring Business Excellence, 1(2), 12-17.
- Scott, J.H. (1976). A theory of optimal capital structure. The Bell Journal of Economics, 7(1), 33-54.
- Terra, P.R.S. (2008). Modigliani, F., & Miller, M.H. (1958). The cost of capital, corporation finance and the theory of investment. American Economic Review, 48(3), 261-297. Revista Base (Administração e Contabilidade) da UNISINOS, 5(2), 154-155.
- Titman, S., & Wessels, R. (1988). The Determinants of Capital Structure Choice. The Journal of Finance, 43(1), 1-19.