Research Article: 2020 Vol: 24 Issue: 3
The Effects of Monetary Policy on Stock Market Returns and Volatility: Evidence from South Africa
Godfrey Marozva, University of South Africa
Abstract
For several decades finance professionals have debated on the effects of monetary policy variables on stock returns. This article examines the extent to which stock returns are linked to interest rate and exchange rate in South Africa from 1995 to 2019, using OLS and GARCH (1,1). Some unanticipated results were uncovered, ultimately contributing to the existing body of literature and illustrating how different markets respond to different stimuli. The most substantial was the significant positive relationship between stock returns and interest rates. A relationship that can be explained by the Keynesian hypothesis based on a sticky price model. In line with theory results revealed a negative and significant relationship between exchange rates and stock market price returns. Also, the study revealed a positive and significant relationship between stock returns volatility and interest rates. However, exchange rates only exhibited a significant positive relationship under the OLS methodology for the JSE All-Share Index return volatility. This study may assist stock market regulating authorities, monetary policy authorities and other stock market participants in understanding the effects of monetary policy variable on stock returns. Further research may dwell on the causality and cointegrating relationships as deterministic relationship may not be dependable for policy formulation and forecasting.
Keywords
Monetary policy, Stock returns, Stock return volatility, GARCH (1,1).
Introduction
Stock market volatility is widely considered pertinent in portfolio evaluation, analysis and management. Changes in monetary policy variables including exchange rates, money supply, and interest rates are perceived to be determinants of stock market volatility. Thus, the monetary policy significantly influences stock market return behaviour, as capital markets play a pivotal role in the transmission of monetary policy (Zare et al., 2013). The higher the volatility of the exchange rate the higher the risk associated with the country and the less attractive it is to foreign investors, consequently this environment is associated with highly volatile and depressed security prices. A decrease in money supply is often associated with an increase in interest rates ceteris paribus. Increase in interest rates increase the discount rates used to calculate the present value of future cash flows. Wang & Mayes (2012) argues that the higher the discount rates the lower the present value of future cashflows and hence the price of the stocks.
Chami et al. (1999) illustrated that the contemporary day process for transmitting the effect of monetary policy shifts is primarily through assets price adjustment instead of through the traditional credit and money channels. Therefore, it is the aim of this article to investigate the effects of monetary policy variables on stock market volatility and stock market returns.
The effects of the monetary policy variables on stock market volatility and returns has been widely researched in the context of well-developed markets (Gallo et al., 2016; Zare et al. 2013; Vähämaa & Äijö, 2011). Most of this literature concludes that monetary policy decision making by the central banks affects volatility and returns of stock markets. The emerging markets are fundamentally and technically different from developed markets (Marozva, 2017). Moreover, the level of efficiency is totally different, it is incumbent to investigate the linkage in emerging markets like South Africa.
Wang & Mayes (2012) opines that a relationship between monetary policy and stock prices is, in fact, prevalent and that the robustness of the inter-relationship is dependent on structural and institutional features of the economy under scrutiny. It is these structural and institutional differences between developed and developing countries that compelled the researcher to investigate the nexus between these variables. Moreover, Belke & Wiedmann, (2018) argues that the nexus between monetary policy and stock prices in an emerging country context is advantageous both to monetary authorities, stock market participants and traders.
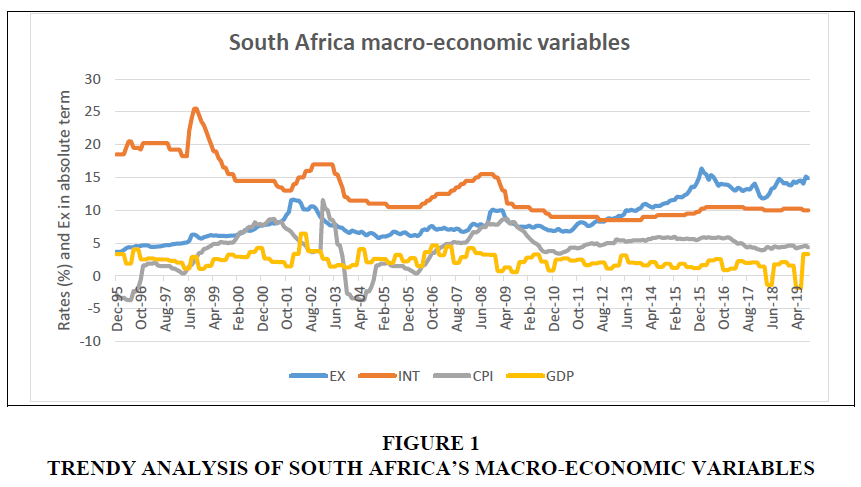
The South African economy is a unique emerging market and new democratic country that attained its independence in 1994. The country has witnessed a significant deterioration in macroeconomic fundamentals since independence. The trend in macro-economic fundamentals are captured is Figure 1.
Over the period of analysis, gross domestic product (GDP) quarterly growth rate was highly volatile and in more recent years the growth rate was negatively skewed. The exchange rate (EX) also high degree of volatility and has been deteriorating since 2010. As the economic activity was shrinking the exchange rate negatively performed. The interest rates (INT) have been going down gradually. A gradual decrease in interest rates could have been resulting from the expansionary policy stance the South African Reserve Bank took in a bid to stimulate the economy. Inflation as measured by consumer price index (CPI) has been highly volatile but below 10% from 1995 to 2010, there after it stabilised around 5%. Despite these interesting economic development in relation to a South African context, there is a dearth of literature and empirical evidence to show the effects monetary policy and other macro-economic variables on the Johannesburg Stock Exchange (JSE). This research, therefore, intends to contribute to this shortage. The objective of this article is to gain insights into the effects of monetary policy variables on the behaviour of stock returns and stock volatility.
Literature Review
Theoretically the linkage between interest rates, exchange rates and stock returns are explained with a couple of models. Kasman et al. (2011) argues that interest rate risk can be an extra market factor on the intertemporal capital asset pricing model (ICAPM) of Merton (1973). This implies that investors will require additional compensation for the risk associated with changes in interest rates. Also, stock market volatility will respond accordingly to changes in interest rates. Kasman et al. (2011), Yourougou (1990) and Sweenery & Warga (1986) point out that interest rates and exchange rates can be analyzed through the implications of the Arbitrage pricing Theory (APT)first studied by Ross (1976). These scholars argue that interest rates and exchange rates are priced factors when stock market prices are in equilibrium. Thus, in equilibrium, changes in interest rates and exchange rates affects stock market prices. Despite a clear theoretical underpinning on the linkage between stock returns, interest rates and exchange rates very few papers investigated the nexus between these variables empirically in emerging markets.
Stock prices are some of the most scrutinized asset prices in most markets and are widely regarded as being hypersensitive to economic deviations given their inherent susceptibility to numerous variables (Wang & Mayes, 2012). The principal set of objectives planned to achieve by the manipulation of monetary policy is illustrated through macroeconomic variables such as economic growth, inflation, exchange rates and unemployment (Aron & Muellbauer, 2007). The ramifications of such findings for monetary policy formulation and investor portfolio approach are pivotal. Reserve Bank officials and stock market observers should be cognisant of the interrelationship between monetary policy variables and share price performance in order to assimilate the effects of policy shifts in a way. It is the responsibility of monetary policy officials to face the often-paradoxical predicament of whether to react to stock price movements, over and above the mandatory response to interest rates and exchange rate developments. Although both reactive and proactive approaches have their merits, timing being the differentiator, both assume that monetary policy can affect stock market value (Umezurike et al., 2019; Mayes & Viren, 2011). Extensive evidence exists reinforcing that, in conjunction with having the ability to influence economic growth and inflation, monetary policy has direct linkage with stock prices (Suhaibu et al., 2017; Iacoviello & Minetti, 2008).
Exchange rates on the other side directly influence companies through their impact on input and output prices. When the exchange rate appreciates the sales and profits of the exporting company shrink, which lead to stock prices declining. The sales and profits of importing companies go up and the stock prices increase. The opposite holds true for depreciating exchange rates. Exchange rates are prices for foreign currencies, and changes in these are reflected in stock prices. In goods markets, an appreciation of the rand may negatively affect the stock prices of exporting companies while generating a positive impact on stock prices of importing companies. Adam & Nguyen (2019), Roubaud & Arouri (2018) and Manu & Bhaskar (2018) showed that the exchange rate exhibited a significant relationship with the emerging and developed stock markets, therefore, the rand/dollar exchange rate was chosen as a variable in this study.
Expectations surrounding monetary policy shifts play an imperative role in the understanding of the market value of financial instruments. Two fundamental hypotheses have been identified by theorists for identifying the role of expectations in financial markets (Sourial, 2002). The first is the Brown & Rozeff’s (1979) adaptive expectations process, where only past information is used to identify the market value of a derivative and history is predictor of the future. The second, a process formulated by Muth (1961) and Lucas (1975), is the rational expectations process, where both past and current information is taken into consideration and understanding market dynamics. A shift towards an expansionary monetary policy approach, according to the adaptive expectations process, will not solicit immediate deviations in derivative prices, and it will take time until investors anticipate an increase in inflation (Sourial, 2002). Conversely, with reference to rational expectations process, investors will anticipate increases in the inflation rate; consequently, prices will increase instantaneously (Sourial, 2002).
Various monetary indicators are used to determine whether a relationship exists between monetary policy shifts and financial market behaviour. The determinants of the validity of the results depend upon the degree to which the market under investigation is mature, and the instruments used by policymakers to cause the shift (Prabu, Bhattacharyya & Ray, 2016). Although there is wide deliberation about the suitability of responding to asset price deviations, specifically share prices, it is apparent that monetary policy does indeed also respond to them in practice, as confirmed by Khan & Saha (2017). The relationship is bi-directional. For stock market participants, vicissitudes in monetary policy variables have implications for pragmatic investment and risk mitigation decisions. For central banks, an understanding of the interrelatedness between monetary policy and asset prices is paramount, as has been demonstrated with emphatic clarity in the 2009 - 2010 global financial crisis. A multifaceted understanding is required for central bankers both to influence stock prices and to influence impact on inflationary and financial stability (Wang & Mayes, 2012).
Methodology
Data and Variables
The study used annual time series data for the period between 1995 and 2019 and all data used in the research was obtained from the McGregor data base and the central bank of South Africa. The analysis pertaining to the deterministic, cointegration and implied causal relationship between the four main variables was restricted to 1995–2019 as the JSE upgraded to an electronic trading system in the early 1990s.
The returns of the stocks were computed as monthly returns of JSE all share index and JSE top 40 index. In order to monitor an entire exchange without the subjectivity of industry, the FTSE/JSE All Share Index and JSE top 40 index were utilised. The FTSE/JSE Africa Index Series is designed to represent the performance of South African companies, providing investors with a comprehensive and complementary set of indexes, which measure the performance of the major capital and industry segments of the South African market. Whereas, the JSE top 40 index represent the top 40 firms listed on the JSE in terms of market capitalisation.
Standard deviation of stock returns was used as a proxy of the stock volatility. The standard deviation is calculated on the returns of the FTSE/JSE All Share Index and the JSE top 40 index for the reasons highlighted in the previous paragraph. Also, Generalised Autoregressive Conditional Heteroscedasticity (GARCH) model was used to establish the effect of the monetary policy variables on the volatility of the stock returns. GARCH (1,1) model was adapted as stock volatility is clustering, that is periods of high stock price volatility are followed by periods of high stock volatility and vice versa.
The lending interest rate is the rate charged by financial institutions on credit facilities to prime customers. This variable is measured as a percentage and is taken as a proxy for nominal interest because it measures the condition of credit in the economy and takes into account central bank’s discount rate and bank’s profit margin. A low lending rate indicates credit and funds are easily obtained, while a high lending rate suggests that funds are more difficult to obtain. The former is an indication of expansionary policy while the latter is an indication of contractionary monetary policy. For the purpose of this research, the South African prime interest rate will be utilised.
For the purpose of this research, the rand and dollar currency movements will be analysed to illustrate the effects that changes in exchange rates have on stock returns and volatility.
Econometric Model
Based on theoretical and empirical discussion, two steps have been carried out to capture the relationship between the variable under consideration. Initially, to establish the deterministic relationship between the variables the Ordinary least squares (OLS) approach was used. Secondly, in a bid to capture volatility clustering associated with the JSE, GARCH (1,1) model was adopted and variables were empirically put into perspective.
Regression Model
JSE all index returns, interest rates, exchange rates, and gross domestic product are incorporated into a function to motivate a linear regression framework in equation 1.
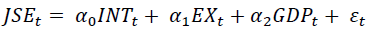 (1)
(1)
For the empirical estimation the relationship between JSE all index stock return volatility, interest rates, exchange rates, and gross domestic were expressed mathematically in equation 2.
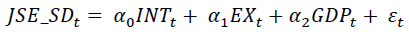 (2)
(2)
To estimate the deterministic relationship between JSE T40-Share index, interest rates, exchange rates, and gross domestic product a linear regression framework was motivated in equation 3.
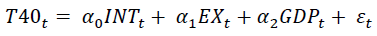 (3)
(3)
For the empirical estimation the relationship between JSE Top 40-Share return volatility, interest rates, exchange rates, and gross domestic were expressed mathematically in equation 2.
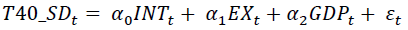 (4)
(4)
Generalised Autoregressive Conditional Heteroscedasticity (GARCH 1,1)
Generalised Autoregressive Conditional Heteroscedasticity (GARCH) method was employed to establish the effect of the monetary policy variables and GDP on the volatility of the stock returns. The GARCH model was the most appropriate model to use as volatility is assumed to cluster that is periods of high volatility are followed by periods of high volatility and vice versa. This is not the case with the simple OLS where the volatility was not lagged. Moreover, Marozva (2017) finds that JSE All-share Index returns are volatility clustering.
The Engle’s (2002) GARCH model was employed to primarily investigate the relationship between JSE stock return volatility and South Africa’s monetary policy variable because of its advantages. Firstly, Marozva and Magwedere (2017) argue that GARCH (1,1) model allows the researcher to observe the pair-wise conditional correlation coefficients for the indices returns under examination. Secondly, the methodology can be used to analyse the relationship between variables for different periods. Lastly, the model gives a better estimation of volatility than standard deviation which does not account for volatility clustering (see Zakoian, 1994; Chen, Gerlach and Lin, 2008). The GARCH (1, 1) models are presented in the following equations and the test results are provided subsequently.
Mean equations (ARCH)
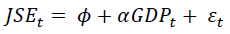 (5)
(5)
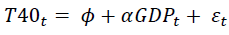 (6)
(6)
Variance equations (GARCH)
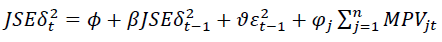 (7)
(7)
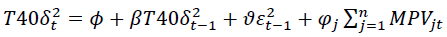 (8)
(8)
Where 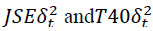 the error terms derived from the lag polynomial model A(L), Φ is a constant, the
the error terms derived from the lag polynomial model A(L), Φ is a constant, the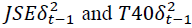 is the squared residual from one period lag of time as derived from the A (L) model which is the previous month’s volatility of JSE All-Share Index returns and JSE top 40-Share Index returns respectively, i.e. the GARCH term in each of these equations, the
is the squared residual from one period lag of time as derived from the A (L) model which is the previous month’s volatility of JSE All-Share Index returns and JSE top 40-Share Index returns respectively, i.e. the GARCH term in each of these equations, the 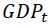 is the gross domestic product for South Africa at a given point in time. the
is the gross domestic product for South Africa at a given point in time. the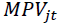 the monetary policy variable j for South Africa at a given point in time, the
the monetary policy variable j for South Africa at a given point in time, the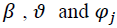 are coefficients and the
are coefficients and the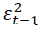 is the previous period squared residual derived from the mean equations i.e. the ARCH term.
is the previous period squared residual derived from the mean equations i.e. the ARCH term.
Analysis of Findings and Discussion
Unit root Tests
To determine the order of integration of the variables of the study, stationarity tests were performed in order to carry out regression analysis and the GARCH (1,1) tests. Since volatility was assumed to cluster, it is vital to assess the stationarity of data series before using GARCH (1,1) model. Moreover, the unit roots were employed for robustness such that no variable that has higher order of integration is included in the regression analysis and GARCH tests. The Augmented Dickey Fuller (ADF) and Phillips – Perron (PP) test of stationarity results are presented in Table 1.
| Table 1 Unit Root Tests | ||||
| Variable | Intercept | Interc & Trend | None | Decision |
| Unit root test using the Augmented Dickey Fuller (ADF) test | ||||
| Exchange Rate | -12.9061*** | -12.8861*** | -12.8011*** | I(1) |
| GDP | -4.6270*** | -5.3372*** | -1.7094*** | I(1) |
| Interest Rate | -7.5477*** | -7.5449*** | -7.5325*** | I(1) |
| JSEAS returns | -17.5821*** | -17.5489*** | -17.0957*** | I(0) |
| Top 40 Returns | -17.9993*** | -17.9747*** | -17.7068*** | I(0) |
| Unit root tests using Phillips – Perron (PP) test | ||||
| Exchange Rate | -12.8599*** | -12.8389*** | -12.7794*** | I(1) |
| GDP | -2.9191*** | -26.8134*** | -20.2810*** | I(0) |
| Interest Rate | -12.2945*** | -12.2290*** | -12.2810*** | I(1) |
| JSEAS returns | -17.6389*** | -17.6039*** | -17.1103*** | I(1) |
| Top 40 Returns | -8.0243*** | -18.0019*** | -17.6803*** | I(1) |
The regression model was then run to investigate the deterministic relationship between the stock returns (JSE All-Share index and JSE Top 40-Share index return/ volatility) and selected macro-economic variables. The F-statistic, t-statistic and P-values were used to establish the best fit of the model and the significance of the relationship between these variables, the results are presented in Table 2.
| Table 2 A Summary of the Determinants of JSE Stock Returns and Stock Volatility | ||||
| Equation 1 | Equation 2 | Equation 3 | Equation 4 | |
| JSE | JSE_SD | T40 | T40_SD | |
| INT | 0.00595* | 0.0170** | -0.00152 | 0.0116 |
| (0.00249) | (0.00605) | (0.00258) | (0.00638) | |
| EX | -0.00256* | 0.0184* | -0.00443* | -0.00366 |
| (0.00217) | (0.00712) | (0.00215) | (0.00645) | |
| GDP | 1.470*** | 1.193*** | 1.204*** | 1.001*** |
| (0.0371) | (0.0918) | (0.0411) | (0.109) | |
| _cons | -1.719*** | -1.775** | -2.471*** | -2.813*** |
| (0.225) | (0.546) | (0.246) | (0.640) | |
| N | 286 | 286 | 286 | 286 |
| R2 | 0.960 | 0.725 | 0.958 | 0.632 |
*p<0.05, **p<0.01, ***p<0.001
According to the results, there is a positive and significant relationship between stock returns and interest rates. Although most existing literature supports a negative relationship between stock returns and interest rates, the results of the researcher are consistent with other empirical research (Kalu, 2017; Ologunde et al., 2007) who explored the association between stock returns and interest rates and finds a significant positive relationship between these variables. A possible theoretical explanation for the positive relationship might be according to Firth (1979) who posits that holding stocks might be an effective hedge against inflation, and hence that the Fisher effect would explain this positive correlation. Moreover, Marshall (1992) states that if inflation is caused by money shock, it would lower the rate of interest and investors would shift their cash holdings to stocks and bonds in order to maximise potential capital gains
Results indicate that there is a negative and significant relationship between exchange rates and stock returns. Theoretically, the relationship can be positive or negative depending on the nature of the companies under investigation. The results of this study are consistent with research conducted by Cifter (2015). Results also show a positive and significant relationship between GDP and stock returns. As expected, the growth in economy is stimulus to the growth of companies in general.
Interest rates, exchange rates and GDP showed to be positively and significantly related to JSE All share index returns volatility. Since the interest rates has shown to be related to stock returns the change in any direction should trigger some activity on the returns of stocks and hence stock return volatility accordingly. Same applies to exchange rates and GDP, a change in these variables had a bearing on the volatility of stock returns. To further analyse the relationship between stock returns and volatility, the generalised autoregressive conditional heteroscedasticity GARC (1,1) model was adopted.
The inferred results of the Z-statistic are based on three types of distribution and these include: Normal Gaussian distribution, Student’s t with fixed df, and the Generalized Error Distribution assumption. The empirical results from the GARCH (1,1) model are presented in Tables 3 and 4.
| Table 3 Z-Statistic for Arch and Garch Test: Dependent Variable (JSE all-Share Index) | |||
| Indep variable | z-statistic | ||
| Normal distribution | Student's t distribution | Gen error distribution | |
| Constant | -0.000003 | 0.000123 | -0.001371** |
| Resid-squared | 0.92498 *** | 1.00791*** | 0.496766*** |
| Lagged Volatility | -0.084310 | -0.070742 | -0.006655 |
| Interest rate | 0.000079** | 0.0000586* | 0.000178*** |
| Exchange rate | -0.000017 | -0.0000153 | 0.000056** |
| Diagnostics | NS/NA/RN | NS/NA/RN | NS/NA |
| Table 4 Z-Statistic for Arch and Garch Test: Dependent Variable (JSE top 40-Share Index) | |||
| Independent variable | z-statistic | ||
| Normal distribution | Student's t distribution | Gen error distribution | |
| Constant | -0.000321 | -0.000310 | -0.001367** |
| Resid-squared | .633983*** | 0.636184** | 0.590760*** |
| Lagged Volatility | 0.238625 | 0.243216 | 0.133624* |
| Interest rate | 0.000066** | 0.000065* | 0.000233*** |
| Exchange rate | -0.000074 | -0.000072 | 0.000016 |
| Diagnostics | NS/NA | NS/NA | NS/NA |
The Table 3 summarises the Z-statistic for ARCH and GARCH test for Exchange rates and interest rates factors relative to the JSE All Share Index. Results showed that the GARCH effect is not significant under all the distribution models. This indicated that though JSE All Share Index volatility was not persistent meaning that the period (t-1) stock returns volatility did not significantly influence stock returns volatility at time (t). The ARCH coefficient is significant under all the distributions an indication that previous period mean stock returns residuals had influence on the current period stock returns volatility. Lastly, results from Table 4 further indicate that interest rate is positively and significantly related to volatility. This indicates that interest rates influence stock market price volatility, the higher the interest rates the higher the volatility. Thus, JSE All Share stock returns volatility is heavily dependent on the interest rate, confirming the finding by Gallo et al. (2016) that high interest rates are associated with high volatility. The reason for the positive relationship could be a result of gradually decreasing interest rates in South Africa. A steady decrease in interest rates could have meant a steady increase stock returns and hence low volatility.
The Table 3 summarises the Z-statistic for ARCH and GARCH test for relationship between the JSE Top 40-Share Index volatility and the selected monetary policy variables. Results showed that the ARCH coefficient is significant under all the distributions, this confirmed that the previous period mean stock returns residual influenced the current period of JSE Top 40-Share Index volatility. The GARCH effect is significant under the generalised error distribution. An indication that the JSE Top 40-Share Index volatility was persistent meaning that the period (t-1) stock returns volatility significantly influenced stock returns volatility at time (t). Lastly, results from table 3 further indicate that interest rate is positively and significantly related to volatility across all z-statistic distribution. Thus, interest rates positively influenced stock market price volatility, implying that the higher the interest rates the higher the volatility. This is in line with results in Table 2, also, confirming the preposition that high interest rates are associated with high volatility.
Conclusion
The main aim of this study was to empirically test the effects of interest rates and exchange rates on stock returns and stock returns volatility. A detailed analysis of the data was undertaken in South Africa from 1995 to 2019. The analysis was done using two econometric frameworks which included OLS and GARCH (1,1) models.
The results on the effects of the monetary policy variables on stock returns were a mixed bag. Contrary to many empirical and theoretical literature the results of the analysis reveal that there is a positive significant relationship between stock returns and interest rates. With reference to exchange rates, the results showed a negative and significant, relationship to stock market price returns, and this was expected and in line with theory. GDP was used as a control variable and the results were as expected, a significant positive relationship was revealed between stock market returns and GDP. Further analysis on the relationship between stock return volatility and the variables under consideration revealed that whether volatility is measured as standard deviation or under the GARCH (1, 1) scenario the results were the same on the effects of interest rates. The results revealed a positive and significant relationship between stock returns volatility and interest rates. However, exchange rates were only positive and significant under the OLS methodology for the JSE All Share Index return volatility.
This study assists stock market regulating authorities, monetary policy authorities and other stock market participants in understanding the effects of monetary policy variable on stock returns. The authorities are advised to monitor the developments in the world financial market, such as movements in major world stock markets and interest rates since they also affect the South African stock market performance. Further research may dwell on the causality and cointegrating relationships as deterministic relationship may not dependable on policy formulation and forecasting.
References
- Aron, J., & Muellbauer, J. (2007). Review of monetary policy in South Africa since 1994. Journal of African economies, 16(5), 705-744.
- Aziza, F.O. (2010). The effects of monetary policy on stock market performance: A cross-country analysis. Available at SSRN 1743834.
- Belke, A., & Wiedmann, M. (2018). Dissecting long-run and short-run causalities between monetary policy and stock prices. International Economics and Economic Policy, 15(4), 761-786.
- Brown, L.D., & Rozeff, M.S. (1979). Adaptive expectations, time-series models, and analyst forecast revision. Journal of Accounting Research, 341-351.
- Chen, C.W., Gerlach, R., & Lin, E.M. (2008). Volatility forecasting using threshold heteroskedastic models of the intra-day range. Computational Statistics & Data Analysis, 52(6), 2990-3010.
- Cifter, A. (2015). Stock returns, inflation, and real activity in developing countries: A Markov-switching approach. Panoeconomicus, 62(1), 55-76.
- Cosimano, M.T.F., Fullenkamp, C., & Chami, M.R. (1999). The stock market channel of monetary policy. International Monetary Fund, Washington DC.
- Firth, M. (1979). The relationship between stock market returns and rates of inflation. The Journal of Finance, 34(3), 743-749.
- Gallo, L.A., Hann, R.N., & Li, C. (2016). Aggregate earnings surprises, monetary policy, and stock returns. Journal of Accounting and Economics, 62(1), 103-120.
- Iacoviello, M., & Minetti, R. (2008). The credit channel of monetary policy: Evidence from the housing market. Journal of Macroeconomics, 30(1), 69-96.
- Kalu, K. (2017). A Re-examination of the asymmetry between interest rates and stock returns. International Journal of Economics and Finance, 9(6), 23-30.
- Kasman, S., Vardar, G., & Tunç, G. (2011). The impact of interest rate and exchange rate volatility on banks' stock returns and volatility: Evidence from Turkey. Economic Modelling, 28(3), 1328-1334.
- Khan, G.S., & Saha, M. (2017). Monetary variables and stock market returns–the indian experience. Research Bulletin, 43(1), 135-154.
- Lucas Jr, R.E. (1975). An equilibrium model of the business cycle. The Journal of Political Economy, 1113-1144.
- Manu, K.S., & Bhaskar, P. (2018). Effect of exchange rates volatility on stock market performance. Asian Journal of Management, 9(4), 1337-1341.
- Marozva, G. (2017). Africa stock markets cross-market linkages: A time-varying dynamic conditional correlations (DCC-GARCH) approach. Journal of Applied Business Research (JABR), 33(2), 321-328.
- Marozva, G. (2017). An empirical study of liquidity risk embedded in banks' asset liability mismatches, Doctoral dissertation, University of South Africa, Pretoria
- Marozva, G., & Magwedere, M.R. (2017). Macroeconomic variables, leverage, stock returns and stock return volatility. Acta Universitatis Danubius. Œconomica, 13(4).
- Marshall, D.A. (1992). Inflation and asset returns in a monetary economy. The Journal of Finance, 47(4), 1315-1342.
- Merton, R.C. (1973). An intertemporal capital asset pricing model. Econometrica: Journal of the Econometric Society, 867-887.
- Muth, J.F. (1961). Rational expectations and the theory of price movements. Econometrica: Journal of the Econometric Society, 315-335.
- Nguyen, V.H. (2019). Dynamics between exchange rates and stock prices: Evidence from developed and emerging markets. The International Journal of Business and Finance Research, 13(1), 73-84.
- Ologunde, A.O., Elumilade, D.O., & Asaolu, T.O. (2007). Stock market capitalisation and interest rate in nigeria: A time series analysis. Economic and Policy Review, 13(2).
- Prabu, E., Bhattacharyya, I., & Ray, P. (2016). Is the stock market impervious to monetary policy announcements: Evidence from emerging India. International Review of Economics & Finance, 46, 166-179.
- Ross, S. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory, 13(3), 341-360.
- Ross, S.A. (2013). The arbitrage theory of capital asset pricing. In Handbook of the fundamentals of financial decision making: Part I (pp. 11-30).
- Roubaud, D., & Arouri, M. (2018). Oil prices, exchange rates and stock markets under uncertainty and regime-switching. Finance Research Letters, 27, 28-33.
- Sourial, M.S. (2002). Monetary policy and its impact on the stock market: The Egyptian case (No. 0204002). Economic Working Paper, Archive EconWPA.
- Suhaibu, I., Harvey, S.K., & Amidu, M. (2017). The impact of monetary policy on stock market performance: Evidence from twelve (12) African countries. Research in International Business and Finance, 42, 1372-1382.
- Sweeney, R.J., & Warga, A.D. (1986). The pricing of interest?rate risk: Evidence from the stock market. The Journal of Finance, 41(2), 393-410.
- Umezurike, C.M., Echekoba, F., & Ananwude, A. (2019). Does monetary policy affect stock market return? recent evidence from nigerian stock exchange (1986-2018). South Asian Journal of Social Studies and Economics, 5(3), 1-8.
- Vähämaa, S., & Äijö, J. (2011). The Fed's policy decisions and implied volatility. Journal of Futures Markets, 31(10), 995-1010.
- Wang, S., & Mayes, D.G. (2012). Monetary policy announcements and stock reactions: An international comparison. The North American Journal of Economics and Finance, 23(2), 145-164.
- Yourougou, P. (1990). Interest-rate risk and the pricing of depository financial intermediary common stock: Empirical evidence. Journal of Banking & Finance, 14(4), 803-820.
- Zare, R., Azali, M., & Habibullah, M.S. (2013). Monetary policy and stock market volatility in the ASEAN5: Asymmetries over bull and bear markets. Procedia Economics and Finance, 7(1), 18-27.
- Zakoian, J.M. (1994). Threshold heteroskedastic models. Journal of Economic Dynamics and control, 18(5), 931-955.