Keywords

Compounding Interest, Retirement Planning, Excel, Economic Education.

Introduction

This paper introduces a lesson on the application of interest compounding and future value calculations to retirement planning. By applying the material to the concept of retirement planning this lesson adds a new dimension to ordinary coursework on these ideas. Students are very interested in this topic and seem to become more engaged with the core material of interest compounding through this presentation. What follows is a unit that can be taught to students with little previous experience in compounding interest calculations or can be adjusted to a more advanced audience. The lesson includes a homework assignment with some out-of-classroom student research and more personal explorations of expected lifespan with an online longevity calculator, projected future living expenses and potential ways to save money. In total, students come away with a much stronger understanding of the ‘magic’ of compounding interest and how it can be used to their advantage to create their own future financial stability.

This lesson draws on retirement information taken from a variety of sources, most notably work done by Littell, Hopkins, Tacchino (2015), Tacchino (2013) & McLellan (2012) Those authors suggest approaches and ideas that need to be considered by retirement planners and their clients (some beyond the scope of short lessons such as this one) but constitute a valuable resource for further information on these topics. The primary concern of this lesson is to demonstrate the power of interest compounding on a stream of deposits to accumulate a retirement fund that can then be drawn down over the retirement horizon, using the basic concepts of future and present value. Additional concerns, such as an analysis of retirement savings vehicles (IRAs or 401(k) plans), Medicare or tax implications of retirement savings can be assigned as student research questions on the student assignment or can be alluded to briefly in class or omitted altogether. The basic components of the lesson, excluding these more in-depth concepts, can be contained in a 1 to 1.5 h class timeframe. While this may require trade-offs with other class material (as all lessons do), it can have valuable life-long impacts on students.

This module should follow on the heels of a lesson on interest and present/future value calculations. At the very least, the concepts of future and present value need to be touched on before this lesson begins. This module requires at least one homework assignment given before the in class presentation and at least one full class period devoted to discussing the results from that assignment as the students present their answers. The lesson involves the presentation of an Excel workbook (available from the author) that demonstrates a stream of savings through working years up to retirement age and then drawdown of the resulting savings balance by month. For more adult students, a brief concluding discussion on opening an IRA account, through something like an on-line brokerage house and a final debriefing brings the lesson to full closure.

Pre-Presentation Class Preparation: Concepts Of Present/Future Value

Topics that need to be covered in class before the lesson are:

1. Present and Future Values of a Single Fixed Amount.

2. Compounding Interest on Streams of Payments.

3. Real versus Nominal Returns.

Covering future value calculations of a single fixed amount is fairly straightforward and introduces the concept of compounding interest. Any number of sources for this material can be found including most economics textbooks (such as Croushore, 2015). Beginning with simple interest calculations using annual interest rates and time in years for a single deposit is common. Equation 1 shows the future value formula for a single current amount (Present Value) with interest rate of r for amount of time t (where r is the periodic interest rate r and t is the number of periods so that if r is an annual rate then t is the number of years).

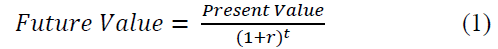
Developing this lesson in the normal fashion to more frequent compounding furthers the understanding of the power of compounding interest rates. The lesson below requires at least monthly compounding of an income stream, so the equation adjusted for monthly compounding (so that r is replaced by the monthly interest rate and t is replaced by the number of months) also needs to be presented and discussed in class prior to the exposition of the retirement section. Extending the concept to a stream of identical deposits made on a regular basis then follows

Equation 2 shows the future value of a stream of monthly deposits (D) for the number of months (m) where r remains an annual interest rate, so that 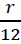is the monthly interest rate.

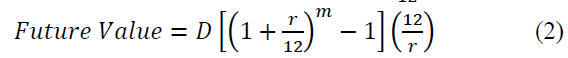
For more advanced students, continuous compounding for a single current amount is based on the formula below with r being an annual interest rate and t in years for a single, fixed initial amount (Present Value) is shown in equation 3.

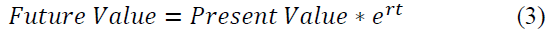
Extending the analysis to a stream of deposits with compounding interest, where variables are as previously defined is demonstrated in equation 4.

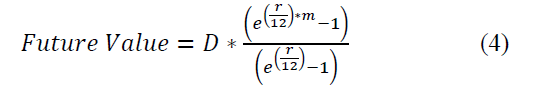
Another concept of importance here is real versus nominal values. Students will, as part of the assignment, be exploring predictions for inflation rates and market rates of return so as to find real interest rates. A brief discussion of inflation adjusted values, using real interest rates rather than nominal rates allows the class to remove focus from price level adjustments to real values. The pertinent relationship between real and nominal values is below. Figure 1 provides a short example of a discussion of price adjustments for inflation.

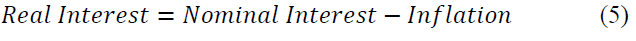
The instructor needs to do some out of class preparation before the classroom presentation of the Excel spreadsheet and the accompanying classroom discussion. Besides personally investigating the answers to all of the assigned research questions, the instructor would do well to provide some outside material. For instance, finding current information on any new Social Security legislation is helpful as students may ask about the topic. Additionally, having information on how to open and the returns to, a few different retirement account options is useful. One place for such information is an online brokerage house. Preparing and assigning the student assignment discussed below and familiarity with the Excel spreadsheet are also necessary.

Student Assignment

The assignment for this lesson needs to be prepared and distributed with enough lead time for students to be able to complete the assignment before the in class demonstration. Setting the due date to coincide with the in class demonstration leaves the material fairly fresh in the minds of students. When the homework is assigned, students should be warned to keep copies of their answers, as they will share their results with the class after the papers have been collected.

The student assignment contains four questions. The first three questions are identical for every student. The first question directs each student to find an estimate of their personal life expectancy. Provide a link to a lifespan calculator such as ‘Living to 100’ (http://www.livingto100.com) or from Abaris (http://www.myabaris.com/tools/life-expectancy-calculator-how-long-will-i-live/). Both of these life expectancy calculators provide an expected lifespan based on current age and a fairly short set of questions regarding health and lifestyle. Most students will find about the same life expectancy given they are currently around the same age. Some students, however, may be surprised to discover the size of the impact of some of their behaviours (such as drinking or smoking).

The second question asks each student to find ways that they, personally, could save at least $15 per week without moving to a cheaper living accommodations or changing jobs (so that they need to think about every day spending habits). The third question asks students to estimate their future living expenses in retirement (in current dollars). For this question, having students concentrate on specific categories of expenditures by wording the question as follows works well:

Estimate how much money you will need to live per month when you retire (in current dollars). Write out how much you think you will need for each of the following categories: rent/mortgage (include an estimate of property taxes if you plan to own a home, at a rate of XX% per year of the home’s value), food, entertainment, transportation, auto and health insurance and additional expenses such as clothing or charity and total it up.(note: the ‘XX’% estimate should be based on your state’s average property tax rate which will be between 0.28% for Hawaii and 2.38% for New York).

Finally, each student gets one research question such as those attached in Appendix A of this paper. These questions involve issues specific to retirement planning. For lower division or introductory courses, it is sufficient to limit these questions to finding expected inflation rates, expected returns to various market indexes or general explorations of retirement issues. The more advanced questions such as 401(k) plans versus Roth IRAs versus Traditional IRAs or Social Security pay-outs at full versus early retirement ages, can be reserved for more in depth personal finance classes or more advanced students. Depending upon the number of students in the class, individualized assignments can be created so that small groups of 2 to 3 students get identical assignments. Having more than 1 student with the same research question, without being aware of who else has that same question, is likely to ensure at least one correct answer. Furthermore, the instructor needs to keep track of which student has which research question so that those individuals can be called upon during the class demonstration. The instructor will want to track the response quality of the answers on the research questions (assigning points on an easily manageable scale, say 0 for no answer, 4 for adequately prepared correct answer and 5 for excellent and thorough response).

Excel Spreadsheet

The instructor will present an Excel spreadsheet for the in class portion of the lesson. There are two versions of the spreadsheet available from the author, one uses monthly compounding analysis while the other uses continuous compounding. While continuous compounding is more realistic, if students are not familiar with continuous compounding using the monthly compounding format for the class demonstration may be more appropriate. The instructor should work with the spreadsheet in advance, perhaps using the SOLVER function, so that the in class presentation goes smoothly.

In Class Demonstration

The in class demonstration has the following steps:

1. Going over homework answers to motivate the concept of retirement.

2. Introducing the concepts of retirement savings and Social Security.

3. Using the homework answers to develop the Excel spreadsheet results.

4. Debriefing.

First Homework Question Discussion

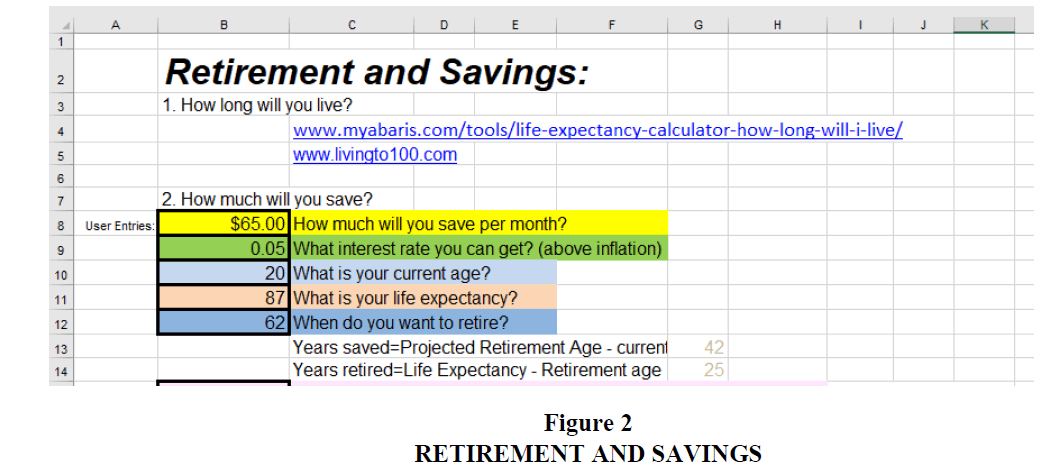
An initial discussion of the first homework question provides estimates on expected lifespan. The instructor can offer his/her own expected lifespan from one of the calculators or ask for student input. Many of the students will have similar results with an expected lifespan of something like 76 for males and 81 for females. Asking for the longest expected lifespan estimate will be useful for the presentation. Upon getting estimates of expected lifespan, ask students when they want (or expect) to retire. The answers may be surprising: ranging perhaps from age 50 to ‘never.’ Open the Excel spreadsheet to the first sheet (Savings) and enter in the approximate current age of most students and the longest lifespan that was mentioned in class (cells B10 and B11, respectively). Enter an expected (realistic) retirement age such as 62 in B12. The sheet will automatically calculate the number of years available for saving (Years saved in cell G13) and retirement duration (Years retired in cell G14).

Second Homework Question Discussion

Student responses for the second homework question, finding ways to save $15 per week, also can prove enlightening to see what some students consider optional spending. Responses will range from eating out less often to reducing impulse shopping binges. In cell B8 enter 65 to represent the monthly total savings for $15 per week with an average of 4.33 weeks per month (a larger amount can be easily substituted later in the presentation so students can see the large difference toward the total retirement account a few extra dollars a month makes). Figure 2 shows the spreadsheet with the default values of $65 a month in savings, current age of 20, life expectancy of 87 and expected retirement age of 62. This figure also lists a default after inflation (real) interest rate on savings of 5% (which will be discussed later in the class discussion).

Retirement Concepts

The ideas of retirement savings and social security are now ready to be introduced. Social Security is often in the news, so students may have ideas they wish to share here. The instructor now presents the current Social Security rules and pay-outs. For instance, retirees are required to have 40 credits or 10 years of work history covered by social security in order to be eligible to receive payments (assuming one is born after 1929). Further, individuals can take early retirement at 62 with permanently reduced pay-outs with full pay-outs being achieved at full retirement age (67 for individuals born in 1960 or later). The Excel spreadsheet (sheet 3) reports minimum social security pay-out amounts for various numbers of years of work (with actual pay-outs likely exceeding these minimum values depending upon income history).

A projected amount for Social Security payments is entered in B22 (set at $1,700 as default to represent a not unobtainable value for full time workers over a career horizon, though this can be easily adjusted downward to a minimum value found in the provided sheet 3 or upward to represent higher future earnings. Further, have students contribute ideas about other sources of retirement funds such as pensions (which are becoming rare, but are still possible) or inheritance. Those amounts can then be entered into the spreadsheet as well.

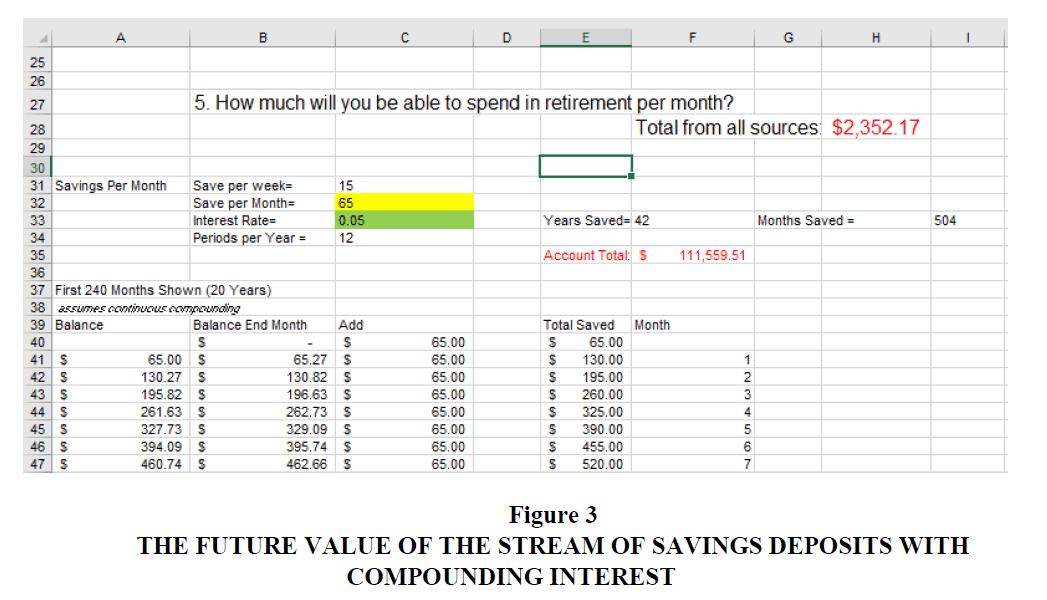
At this point, the instructor should bring into the discussion the previously discussed topics of the future value of a stream of deposits with compounding interest rate calculations. How these formulas translate into Excel should be left to more advanced students with some experience in Excel (Excel formulas for both monthly and continuous compounding are included in Appendix B). Figure 3 shows the future value of the stream of savings deposits with compounding interest as the account total in cell F35 and monthly spending available as drawdown from that amount plus social security income in cell H28 with 0 inheritance and 0 pensions as defaults. Exploration of the spreadsheet that shows the total of savings in column E (apart from interest accumulation) as compared to the total amount in the account (including interest accumulation) demonstrates the power of compounding interest.

A further demonstration of the power of compounding interest is now easily done by changing the amount saved from $65 a month to something higher while watching the account total (cell F35) and available monthly spending (cell H28) jump upwards. For instance, adjusting savings per month to $150 increases the total value in the account to over a quarter of a million dollars and monthly spending to over $3,200. A brief discussion of saving before spending (putting money into a savings account automatically) beginning early in life can be beneficial here.

Third Homework Question Discussion

The third homework question now comes into play. That question asks students to estimate their income requirements during retirement. Students will likely offer many different amounts from very low levels of spending to over $10,000 a month. For students already comfortable with Excel, an experiment with SOLVER can have Excel go backwards from the amount a student wants to live on to the amount that must be saved per month (Appendix B). Without the use of SOLVER, it is still useful to change the monthly savings amount in cell B8 manually a few times to demonstrate how different savings amounts affect the account totals and the available monthly spending amounts.

Fourth Homework Question Discussion: Research

The next phase of the demonstration depends upon the various answers to the research questions. A place to begin is to mention the interest rate assumed in the Excel spreadsheet (5% here). Research question 1 asks for the average index fund return projections. Students will usually come up with an annual rate for the S&P 500 or Dow of something like 9%. Bring in the results from research question 2 (inflation estimates), to find a real return for the average return from question 1. Change the Excel spreadsheet based on the student information. As the real return estimated in this way will still be quite high, the instructor might bring in current returns on a retirement account such as an IRA to compare to a much lower rate. The additional information from research question 2 where students are asked what the inflation rate was between 1974 and 1981 and then from 2009 to 2010 brings in the ideas that inflation rates may vary dramatically from the fairly stable rates seen in recent years. Try adjusting the real rate of return by various levels of inflation in the spreadsheet to demonstrate how important inflation is to planning.

Additional research questions will vary depending upon the class level and previous preparation. For a fairly low level class, these first two questions and the question on ‘good’ places to retire can wrap up the presentation. For the more advanced classes, research questions dealing with 401(k) or IRA types and tax treatment of retirement income and questions on mortgages and Medicare can bring the discussion to a deeper level (though at the expense of at least 20 minutes of class time).

After Class Demonstration Debriefing

After the in class demonstration, students need to be debriefed on their take-away from the lesson. The traditional methods of asking the ‘What’, ‘So What’ and ‘Now What’ questions can work well. Such questions as ‘What did you find most surprising about this presentation?’ or ‘What do you think about how much you need to save and your needs for retirement income?’ explore what students actually understood. ‘Do you think you will start a retirement account when you start your first full-time job?’ also get at student impact. This discussion can occur at the end of the period, if time allows or at the beginning of the next class.

Another method for debriefing students is to use an assignment of one or more debriefing questions such as an essay due the following period. For instance, asking students to reassess their answer to the homework question 3 (how much a student thinks they will need to live on) and then use a copy of the Excel spreadsheet to find the amount of monthly savings required to cover that expenditure (students that are not able to use SOLVER will likely use trial and error to find the savings amount) provides students with some introspection on these topics. An extension to that question is to use the estimate of savings necessary to meet their retirement spending goals to find the salary they would need if savings were to be no more than 20% of income.

Summary

This paper has focused on providing a module on retirement planning that could be used in any course that offers present/future value and compounding interest instruction but most particularly in a course with a personal finance component. This lesson makes use of an Excel spreadsheet to demonstrate the power of compounding interest on a stream of deposits used toward retirement funding. There are extensions for students who are more advanced and can understand continuous compounding or those who are facile with Excel programming. Instructions for the teacher for preparation, a student assignment and extensions of the basic material are included along with various methods of student debriefing.

Many of the students who have participated in this exercise have shown long lasting impacts. Over the years, students have reported that they were motivated to max out their employer matching retirement options beginning with their first employer and a few students even opened their own IRAs before graduation. In essence, this demonstration has changed the lives of many students.

Appendix A

Student Homework Research Questions

1. Find a projected index fund long term average (average return on the S&P 500, Dow Jones Industrials or other market measure, with a long term future projection) (cite your source). How much would a $50 investment today be worth in 30 years if invested at the rate you found?

2. Find an estimate for annual inflation rates in the US for the next several years (cite your source). Compare this to the average annual inflation rate for the US from 2009 and 2010. Next find the average annual inflation rate in the US from 1974-1981.

3. Explore what states are considered most ‘Retirement Friendly’ and present two such states and the reasons why they are supposed to be good for retirees.

4. Describe the differences between a 401(k) plan and an IRA. What type of employment is likely to offer a 401(k) plan? (more advanced students)

5. Describe the tax treatment of Traditional IRA income versus savings account withdrawals. Describe how you can borrow against or make an early withdrawal from a Traditional IRA. Why is an IRA used for retirement? What assumptions make an IRA better for retirement than a regular savings account? (more advanced students)

6. Compare a Roth IRA to a Traditional IRA (compare withdrawal limitations, annual deposit restrictions and any other requirements). What is the advantage to a Roth? Can you borrow from your own IRA before you are 62? (more advanced students)

7. Investigate Social Security tax treatment. Find out how social security payments are taxed at the federal level and your state level. Find out how much ADDITIONAL income (over social security) a person can have before social security pay-out is affected (then tell us BY HOW MUCH social security is affected). (more advanced students)

8. Compare the cost of a 20 year mortgage for a $150,000 home at current rates (with a $30,000 down payment and tax deductible interest, assuming you have an income of $50,000 a year to determine your tax bracket) to a $650 a month apartment rental over the next 20 years. How does your tax burden change if you buy rather than rent? Mention property tax rates and be complete. (more advanced students with previous exposure to mortgage finance)

9. Explore medical care costs. Discover and explain the difference between Medicare Part A, Part B and Part D. Find the current cost of a Medicare Advantage plan in your area and explain how it differs from Parts A, B and D of Medicare. (more advanced students)

Appendix B

Additional Material For Advanced Students

Excel Formulas

For Monthly Compounding

In Excel, there is a built in equation for the future value of a stream of payments. It is:

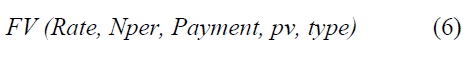
Where, Rate is the monthly interest rate or 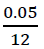in the example above, Nper is the number of periods (months, at 504 in our example), Payment is the monthly savings amount (65, above), pv is 0 meaning there is nothing in the account to start with and type is 0 (payment at the end of the period, rather than at the beginning of the period). This formula produces a negative of what would be accumulated in a savings account (so a simple negative sign in front of the formula turns it into a total value saved).

If the class has had experience with Excel formula writing, using the actual formulas from class can be used to reinforce the class material. The formula entered into Excel that is the direct ‘translation’ of the monthly compounding formula from equation (2) above, using the values from our example, is:

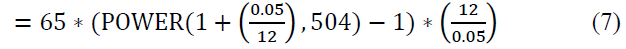
For Continuous Compounding

For a continuous compounding situation, following equation (4) above, the Excel formula for the future value of a string of deposits of $65 per month, continuously compounded, with an annual interest rate of 0.05 for 504 months is:

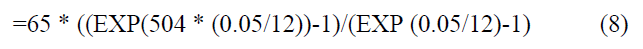
Solver

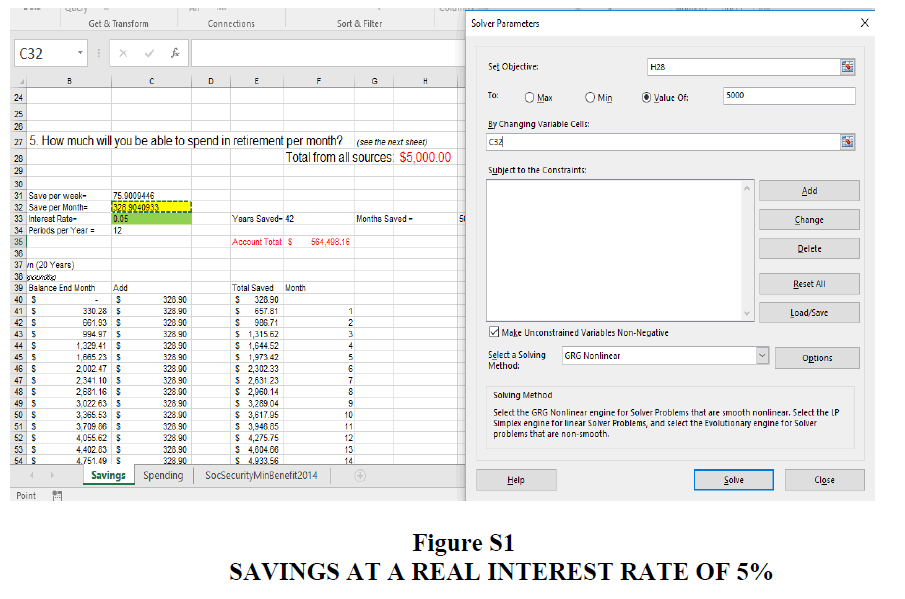
SOLVER is an Excel Add-in that can work backwards from a desired result to determine required input values. In this lesson, SOLVER can be used to find the amount of monthly savings necessary to support a particular target retirement income. In Excel, SOLVER is not included with the recommended installation but can be easily added. Installing SOLVER is done by following Menus – File – Options – Add-ins – (highlight SOLVER Add-in) – click OK. To find the required monthly savings to support a fixed pay-out, open SOLVER by going to the Data tab and click on SOLVER in the ribbon. In the menu that pops up put H28 (the monthly pay-out) in the first box, click on ‘Set Value to’ and enter an amount, say $5,000 and in the last box of the pop up menu ‘By Changing Variable Cells’ put C32 and click on ‘Solve’. The amount of monthly savings necessary to have $5,000 per month available to spend is calculated to be $328.90 for the current example with 504 months available for savings at a real interest rate of 5% (Figure S1).

References

1. Bernicke, T.Y. (2005). Reality retirement planning: A new paradigm for an old science, FPA Journal, 6, 1-8.
2. Compound Interest. (2017). Retrieved November 15, 2017 from http://www.financeformulas.net/Compound_Interest.html
3. Croushore, D. (2015). M&B3. Stamford, CT: Cengage Learning. FV of Annuity with Continuous Compounding. Retrieved November 15, 2017 from http://www.financeformulas.net/Future-Value-of-Annuity-Continuous-Compounding.html
4. Littell, D., Hopkins, J. & Tacchino, K.B. (2015). Planning for retirement needs 13th edition, Bryn Mawr: American College Press.
5. McLellan. & Allen. (2012). Foundations of retirement planning: An overview. Bryn Mawr: American College Press. Available at https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0ahUKEwjy8caPpPDSAhUQ3YMKHdqBACcQFggkMAE&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.469.5007%26rep%3Drep1%26type%3Dpdf&usg=AFQjCNG7LluLHCPi_xQn09KrocY65WcD3g
6. Tacchino, K.B. (2013). Making retirement secure: Innovative concepts for financial advisors. Bryn Mawr: American College Press.