Keywords

Population Ageing, Retirement Age Policy, Pension Systems.

JEL Classifications

H55, J14, J26.

Introduction

In the most industrialized countries since the second half of the 1980s, population aging, short-sighted political pre-commitments and economic slowdown have raised problems in financing pension systems (Börsch-Supan, 2005, 2006; Barr, 2006). Three systemic reforms have been suggested: firstly, the transition to a Fully Funded Defined Contribution scheme (FF, below); secondly, the reshaping of the Defined Benefit pension scheme (DB, hereinafter) and, finally, the establishment of a hybrid pension system as a compromise between DB and FF, namely, the pension scheme that called Notional Defined Contribution pension scheme (NDC, hereafter).

In the literature, two positions emerged regarding structural differences between NDC and DB, the circumstances in which DB can act as NDC and, finally, the possibility of NDC to resolve, once for all, the financial unsustainability of pension systems.

On one side, supporters of NDC maintain that DB and NDC are structurally different from each other since the NDC, unlike DB, manages to isolate pension systems from a multiplicity of risks (Kruse & Palmer, 2006; Palmer, 2000; Settergreen, 2001). The NDC traditional scheme proposed implies that financial equilibrium is achieved by making only the amount of pensions endogenous. In other word, it does not contemplate alternative pension policies that envisage a different distribution of the financial and/or physical burden of the demographic shock between current and future generations.

On the other hand, another group of researchers argues that the structural differences between the two pension systems are not all that stark. Furthermore, it argues both that in NDC political and demographic risks could bring out–similar to what happens in DB–financial unsustainability (Barr, 2004; Börsch–Supan, 2006; Diamond, 2005) and that, through an appropriate remodeling, DB could work just like NDC. Actually, a long time ago and well in advance, Musgrave (1981) showed that a large set of pension policies can be implemented in DB in order to offset economic and demographic shocks. In particular he strongly recommended the introduction of automatic adjustments of contribution and/or replacement rates. However, given the historical context in which Musgrave wrote, he did not consider the impact of the risk of the lengthening of longevity on financial stability of pension systems an issue that has become central to the debate over the last decade.

Finally, in recent years in front of the lengthening of longevity a debate on making the retirement age an endogenous variable in pension systems for ensuring financial stability of the latter has developed. However, no substantial agreement has emerged in the literature on this issue. While some researchers believe that this measure is able to reduce the long-term pension deficit (Magnani, 2016; American Academy of Actuaries, 2007; Liebman et al., 2005; Poole, 2004; Cremer et al., 2006; Pestieau, 2004) others, conversely, affirm that this is an unnecessary political option (Diamond 2005; Diamond & Orszag, 2004).

The purpose of this paper is twofold: firstly, to analyze both structural differences between DB system and NDC system and the conditions under which both can ensure the financial sustainability of pension systems; and secondly, to examine whether the extension of retirement age is a measure able to reconcile the constitutive objective of pension systems i.e., individual well-being, with the long-term financial sustainability of the latter.

The Basic Features of Pension Systems

This section sketches the basic features of pension systems i.e., the demographic structure, the management of pension instrumental variables and, finally, the risks affecting pension systems.

The Demographic Structure

The demographic structure of the economy – represented in Figure 1 recalls that of to the traditional overlapping generation model (Samuelson, 1958 and Diamond, 1965) modified in order to capture the effects of longevity lengthening on the dynamics of pension systems. Economy proceeds with discrete interval where one interval is divided into j sub-interval each of which lasts 1/ j of the interval. Generations are constant i.e.

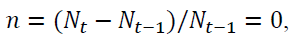
So, that

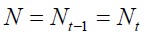
And stay in the economy for two periods. Generation t individuals in the first period work and, in the second period, go through three phases: in the first phase they spend time to continue working; in the second phase they retire and, finally, at the beginning of the third phase they die and leave the economy before the end of the period. From the previous assumptions, it follows that the individual lifespan of generation 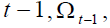which captures the longevity of the individual is divided into one work phase and one retirement phase because, by hypothesis, childhood is ignored. In literature, sometimes, longevity is endogenously determined such as, for instance, by Pestieau et al. (2006) where it depends on health investment. In our model we simply assume that it is exogenously determined.

The retirement age, 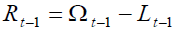defines and de facto coincides with the working phase length which is made up by k sub-periods each of which lasts1 / k.

Furthermore, the retirement age at time 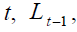is fixed and enforced at the beginning of period 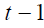when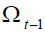 is revealed in previous period; the length of the work phase when is changed for the pensioners of generation 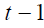it also applies to future generations so that 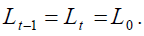Finally, the retirement phase length is divided into h sub-periods each of which lasts1 / h . From the aforementioned assumptions it follows that length of the period in which individuals are not any more in the economy is made up by ω sub-periods each of which lasts 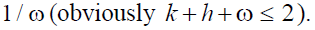It is worth to stress that in this paper the retirement age coincides with the mandatory retirement age. Our analysis does not take into account the issue of early voluntary retirement age often addressed by some authors (Diamond, 2005; Cremer et al., 2006).

Under the above assumptions, it follows that 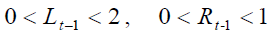and 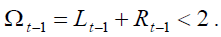We recall that, the subscript on variables 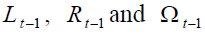refer to generation and not to time. At time t, individuals of generation t receive in advance the full amount of real wage earned during their lifetime.

A measure of the ageing population may be represented by the old age dependency ratio, 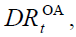which at the time t is equal to the ratio between the number of generation 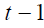retirees adjusted for the duration of their retirement phase, and the number of workers of generation t, adjusted for the duration of their working phase:

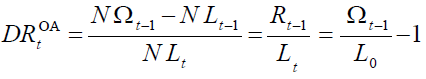(1)

Since 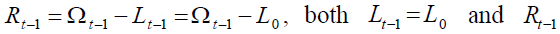are instrumental pension variables, and, as a consequence, 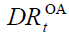is not strictly a demographic variable since it depends on policy makers’ choice about 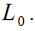By managing 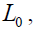policymakers can affect the structure of population by age and, eventually, maintain constant 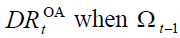changes.

The Management of Pension System

At time t, policymakers must manage the pension system, which has already been set up in previous periods, carrying out two tasks: firstly, to choose the final goals of pension system and to assign priorities if a trade-off will emerge among them; and, secondly, to define a pension policy plan to achieve the final goals. In general, policy-makers with regard to pension systems pursue two final goals: firstly, the constitutive goal of pension systems namely a high level of individual well-being which implies that individuals enjoy a stable level of consumption over time and, secondly, the goal of pension system financial stability i.e., the fulfillment of a balanced budget of the pension system so as to ensure its long-term sustainability.

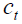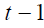In order to achieve the final goals, policymakers must manage the pension instrumental policy variables. On the one hand at time t, a worker of generation t pays contribution in each sub-period of while, on the other hand, at time t, a retiree of generation receives a pension amount 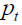in each sub-period of 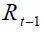where the subscript on the variables 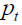and 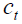refers to time. Obviously, the pension system budget balance, 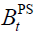, is equal to the difference between aggregate pensions and aggregate contributions:

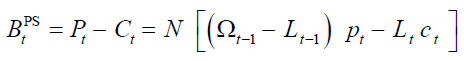(2)

We assume that when a budget deficit occurs, that is 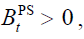it is financed by bonds so that the pension system generates a backward intergenerational redistribution. In conclusion, policy-makers manage three instrumental pension variables 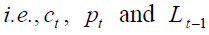(since, given 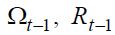is derived accordingly) so that let 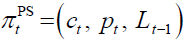be a pension policy plan on a pension system at period t.

The Overall Risks Affecting the Economy

The fulfillment of the two major goals is undermined by demographic, economic and political risks that, in turn, could produce demographic, economic and political shocks.

1. The demographic risk is the uncertainty surrounding the ageing population (in relative term): an increase (decrease) in 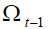– a negative (positive) shock – produces an increase (decrease) in retirement phase as long as 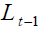does not change.

2. The economic risk is the uncertainty about economic activity: an economic slowdown (growth) – a negative (positive) shock – determines a reduction (increase) in γ.

3. The political risk is the uncertainty surrounding the policymakers’ ability or willingness to manage the instrumental pension variables in order to fulfill the financial goal (for an analysis of political risk see Diamond, 1996; Shaven & Slavov 2006).

The mechanism for determining the amounts of pensions distinguishes two pension schemes: the defined-benefit (DB) and defined contribution (DC) pension scheme.

The Defined Benefit Pension Scheme

In DB, pensions for current retirees are financed through contributions paid by current workers and, moreover, their amount derives from a formula related to gross wage. At time t , on the one hand, in each sub-period of 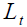workers of generation t earn a gross wage equal to 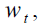whose growth rate is constant and equal to 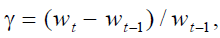and in each sub-period of 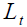pay a contribution 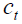for an amount equal to:

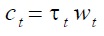(3)

where 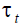is the contribution rate. On the other hand in DB, retirees of generation 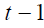receive in each sub-period of their retirement phase a pension 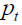for an amount equal to:

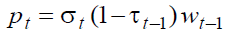(4)

In other words, retirees of generation 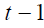receive in each sub-period of their retirement phase a pension for an amount linked to real after tax wage of the previous period through a replacement rate equal to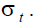

Let us now analyze the effect of the demographic shock on the functioning of the pension system and, furthermore, examine how this shock affects the achievement of the two objectives and whether the policy makers are able to achieve both goals when this shock appears. As we will show, with regard to the latter issue, the result depends on which objective has priority over the other. Two cases are examined: in the first case, policymakers assign priority to the financial goal, in the second one, to the constitutive goal, that is, the well-being of individuals.

The Financially Balanced DB

In the financially balanced defined benefit pension scheme, DB^B,DB, policymakers prioritize the financial goal so that, given (4), equation (2) becomes:

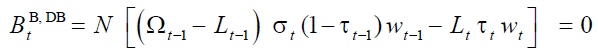(5)

In this pension scheme, equation (5) is a constraint that the pension plan has to satisfy at each period and recalls that the three instrumental policy variables cannot be set independently:

policymakers can choose two, but the third must be left as endogenous variable. Then, at each time t , given 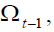the pension policy plan is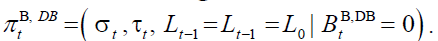

In equilibrium namely when demographic and economic variable do not change, the instrumental pension variables do not change as well. As a consequence the pension policy plan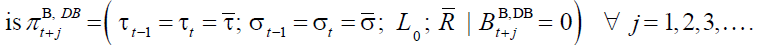

In these circumstances at time t , given equations (3) and (4), the internal factor of return of individual of generation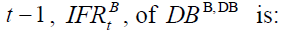

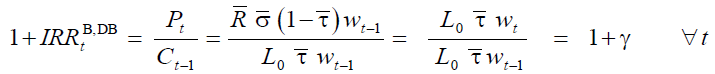(6)

where 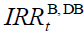is the internal rate of return of both retirees of generation 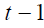and future generations as long as shocks do not occur. Equation (6) shows that the internal return factor that satisfies the balanced budget goal is equal to the growth factor of the tax-base, that, in turn, is exogenously determined by γ irrespective of 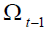. Not surprisingly, it coincides with the Aaron- Samuelson condition, when population is stationary, since DB^B,DB really is the traditional PAYG system (Aaron, 1966; Samuelson, 1958).

Now we analyze the effects of the occurrence of the demographic shock on the working of DB^B,DB. Let us rewrite equation (5) in the following way:

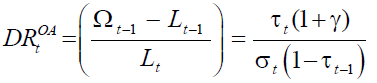(7)

Equation (7) show that balancing the budget requires that two instrumental policy variables to be fixed while the third one is residually derived by (7). Three different pension policy on DB^B,DB corresponds to each instrument policy variable that is left endogenous. Actually, Musgrave (1981) distinguishes four forms of DB^B,DB: fixed replacement rate, fixed contribution rate, fixed replacement rate adjusted, and fixed relative position. By dividing the individual’s life into two parts, our analysis allows to define a further case based on retirement age as an endogenous variable.

The Endogenous Contribution Rate Policy

In the endogenous contribution rate policy on DB^B,DB, whether the demographic variable changes, from 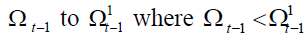the value τ that satisfy the financial goal is derived by equation (7):

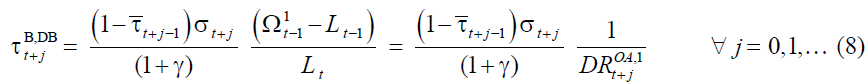
In our model the endogenous contribution rate policy coincides with the “fixed relative position”, favored by Musgrave (1981) since amount of pensions depends on after-tax wage rather than gross wage.

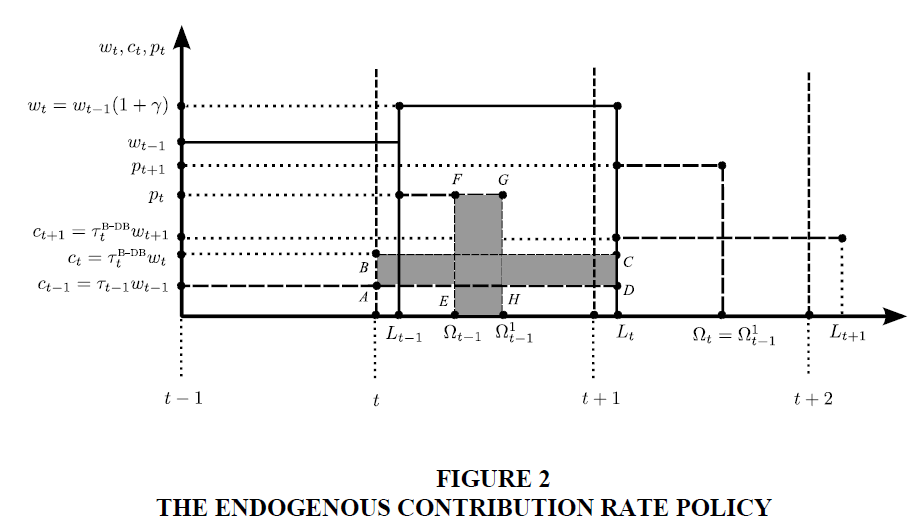
Figure 2 shows the effects of a permanent increase in longevity from 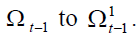At time t since the pension amount t p does not change, aggregate pensions increase for an amount equal to area (EFGH). Since budget must be balanced, aggregate contributions have to increase, via the increase of 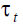, for an amount equal to the increase of aggregate pensions: area (ABCD) = area (EFGH). As a consequence, in period t retirees of generation 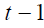are not affected by the negative demographic shock because the increase in the amount of aggregate contributions of generation t workers allows financing the increase in the aggregate amount of pensions. Nevertheless, starting from the next period the burden of the negative demographic shock, in terms of higher contributions, falls on future generations: as a consequence, individuals' wellbeing reduces throughout their entire lifespan.

The Endogenous Pension Amount Policy

When the endogenous amount of pension policy is chosen, changes in the demographic variable 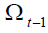impose adjustments on the replacement rate, and therefore, on pension amounts. The equilibrium value of the replacement rate follows from (7):

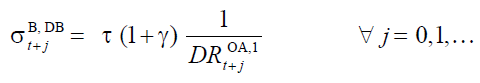(9)

Where, 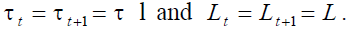Equation (9) represents the automatic rule to counterbalance negative demographic shocks: at each period, the replacement rate equals a constant parameter (that depends on 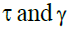) multiplied by the inverse of the old age dependency ratio. From (9) and (4) it follows that the pension amount is equal to:

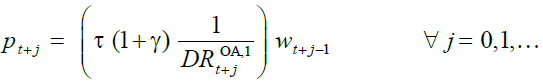(10)

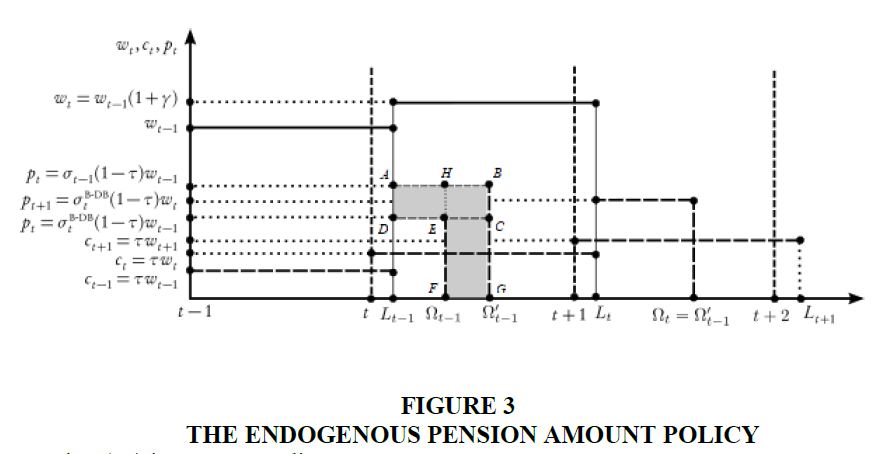
Figure 3 shows the effects of an increase in and, therefore in As a consequence of the negative demographic shock, at time t, as long as the pension amount in each sub-period is maintained constant at the previous level 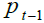the increase in aggregate pension amount due to the increase of 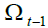is equal to area (HBGF). However because of balanced budget constraint and the constancy of the amount of aggregate contribution, the pension of the sub-period must be reduced so that the reduction of the aggregate pension is equal to area (ADCB) so that area (ADCB) = area (EFGH). In conclusion, under this pension policy the negative demographic shock produces a permanent decrease in pension amount and therefore, also in this case, reduces the well-being of future generations.

The Endogenous Retirement Age Policy

In the endogenous retirement age policy on DB^B,DB, 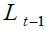adapts to offset adverse changes in longevity, according to the rule that derives from (7):

Rearranging (11) in more appealing terms:

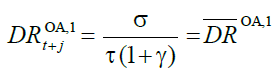(12)

i.e., policymakers by adjusting the retirement age can maintain the population ageing index unchanged. In other words they make the ageing a relative rather than absolute concept.

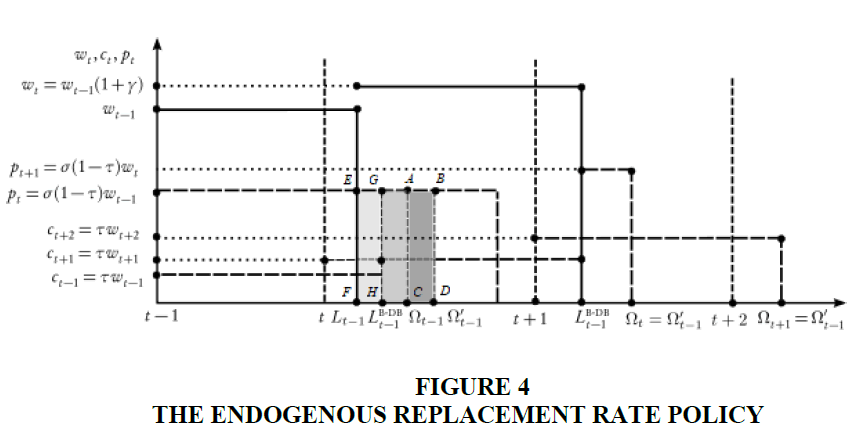
Figure 4 shows that the increase in 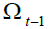produces and increase in the aggregate pension for an amount equal to the area (ABCD). As a consequence – given the balanced budget constraint the contribution and the replacement rates – the retirement age must increase so to reduce the aggregate pension for an amount equal to area (EFGH) where area (ABCD) = area (EFGH).

Summarizing, in DB^B,DB the political risk vanishes since the financial goal has the priority on the well-being of individuals. In these circumstances, the occurrence of a negative demographic shock produces inevitably a burden on individual of current and future generations: a financial burden in terms of greater contributions and/or lower pensions that produce a decrease of the well-being of individuals; a physical burden in terms of a greater working effort in order to maintain a constant the individual well-being.

The Financially Unbalanced DB

In the financially unbalanced defined benefit pension scheme, DB^UN,DB, the balanced budget constraint does not constitute an additional goal. All instrument policy variables are fixed “ad hoc” i.e., 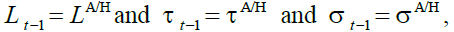while the pension budget balance is left endogenous. We recall that the “ad hoc provision” approach is briefly discussed, and drastically rejected, by Musgrave (1981). It is assumed that ad hoc pension policy produces a budget deficit, DB^UN,DB equal to:

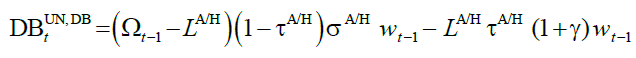(13)

The internal return factor associated with DB is:

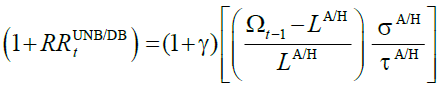(14)

In DB^UN,DB, the internal return factor is affected by instrument policy variables and longevity. Fortunately for current generations, but unfortunately for future generations, current generations are more than fully covered against negative demographic shocks. Longevity, from the current retirees’ view, does not entail a loss. Contrariwise, it results in a nice gain: the more longevity lengthens, the more the internal return factor increases, the better retirees are. The ageing of population, therefore, constitutes an underhand mechanism for redistributing resources, via pension system, from future to current generations.

The Notional Defined Contribution Pension Scheme

In NDC at time t, on the one hand, current retirees of generation receive pensions derived from a contribution related formula (as in FF) and, on the othe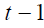r hand, workers of generation t finance those pensions through their contributions (as in DB).

First, at time 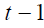, contributions of workers of generation 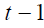plus the interests accrued on the basis of the internal rate of return, 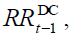fixed exogenously by policymakers, are recorded on an individual notional account. World Bank (2001), labeled this pension system the “third way” between DB and DC. For a comprehensive analysis of NDC see Palmer (2000). For a general classification of pension systems see Lindbeck & Person (2006). Second, at period t, individuals of generation 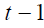enters in the retirement period with an endowment of notional capital, 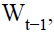equal to:

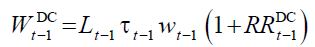(15)

And receive a pension amount equal to the ratio between the notional capital, and the length of the retirement life:

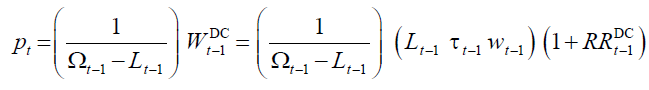(16)

In NDC the pension system budget 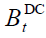is given by:

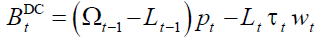(17)

Equation (17) does not imply per se a balanced budget, until the pension policy is defined. In NDC policymakers control the internal rate of return, so that the pension policy plan is 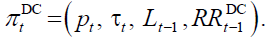In a similar way to DB, in NDC both pension amount and budget balance depend on which goal has priority on the other.

The Financially Balanced NDC

In financially balanced notional defined contribution pension scheme, NDC^B, policy ensures a balanced budget continuously:

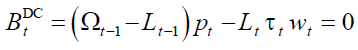(18)

And, as a consequence, a backward intergenerational redistribution is ruled out by definition. Fulfilling this task requires a two-steps decision-making process.

In the first step, the internal return factor must be fixed. Given (18) it follows that in equilibrium, 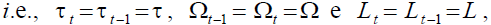it must be:

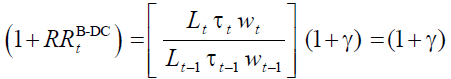(19)

Hence the feasible internal return factor is equal to the growth factor of the taxation base.

In the second step, the recognition of an automatic adjustment rule is needed to satisfy the balanced budget constraint continuously. However, once the internal return factor has been fixed, the pension amount does not necessarily need to be endogenous. Indeed, from equation (18) it follows that in the NDC^B, the pension amount is equal to:

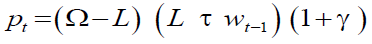(20)

And that one instrumental policy variable must be left endogenous. Tracing the taxonomy used for DB on NDC, three alternative pension policies can be identified.

The Endogenous Contribution Amount Policy

Suppose now that the demographic variables change from 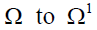where 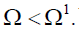When policymakers consider the contribution rate as endogenous, such rate adjusts according to the following rule, obtained from (18):

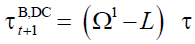(20)

In other words, if longevity increases, in order to keep the amount of the pension equal to the level preceding the negative shock, the notional capital must increase through an increase in the contribution rate in order to neutralize the negative effect on the amount of the pensions. Thus, this approach implies that the demographic shock falls on future generations in terms of higher contributions and, therefore, in terms of a lower level of individual well-being.

The Endogenous Pension Amount Policy

In the endogenous pension amount policy on NDC^B, since 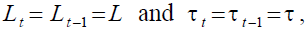there must be:

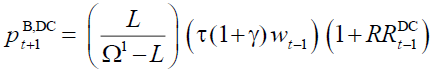(21)

This is the conventional rule that developed in the literature and implemented in some countries. Equation (22) shows that the demographic risk fall entirely on current retirees in terms of lower pension amount. Even during the retirement period, the balanced budget constraint requires to adjust pension amounts to changes in life expectancy.

The Endogenous Retirement Age Policy

When the retirement age is endogenous a negative demographic shock results the policymakers must increase the value of then from (18) and given (15) and (16) it follows the retirement age that satisfy equation (18):

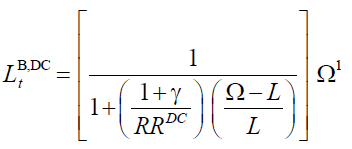(22)

As a consequence, when the retirement age is endogenous the lengthening in longevity implies an increase in the retirement age since the term in the square bracket is constant: the workers of future generations will bear the costs in terms of later retirement whereas the wellbeing of individual is not affected.

This automatic adjustment rules have not been worked out in the recent literature, even if they do not seem incompatible with the key features of NDC. Indeed in front of external shocks the choice of the retirement age as an endogenous variable is an attractive response to contrast the steady lengthening of longevity. Actually, it allows overcoming the trade-off between longrun financial solvency and maintenance of the standard of living.

Equivalences and Differences between NDC and DB Plans

Let us conclude discussing the basic differences between NDC^B and DB^UN,DB. At the end, the final core difference between them stays with the decision-making process rather than to the simple mechanism of generating the pension amount. On one side, in a NDC^B system, the contribution related formula for generating pensions is built-up on two key elements of the decision-making process notably which of a balanced budget constraint, internalized in the pension plan and that of an explicit automatic adjustment rule. Contrariwise, in a DB^UN,DB system, pensions are fixed in direct ratio to the workers’ real wage irrespective of whether the balanced budget constraint is satisfied or not, and furthermore the system does not adjust automatically to demographic and economic shocks.

When DB^B embraces the same decision-making process as NDC^B, (i.e., the same reaction – based on an automatic rule to external shocks for maintaining balanced budget) then both pension systems possess the same properties and perform identical outcomes in spite of the fact that they use a different mechanism for computing pensions. At the end, the difference reduces to the outward appearance of this mechanism. World Bank (2001), Börsch–Supan (2006) sketch out roughly this point. Cichon (1968 & 1999) went further and showed the equivalence between DC and DB with respect to the endogenous pension policy.

The Financially Unbalanced NDC Pension Scheme

As we have seen, the contribution related formula for computing pension amount is not a sufficient condition to guarantee the financial stability of NDC. Indeed, discretionary policy decisions are required frequently during the decision-making process. They concern three main elements: the choice of the internal rate of return, the proper fine-tuning of the automatic adjustment rule and, finally, its effective enforcement of the latter. Obviously, when the theoretical conditions are met, the financial sustainability of the pension system is guaranteed. In the real world, however, NDC is also affected by the political risk as well as the other pension systems.

Let us now examine the two main sources of political risk that are still active in NDC. The literature largely points out the necessary conditions to align the effective design to the theoretical model: firstly, the internal rate of return must be set equal to the salaries growth rate; and secondly, the frequency of updating the automatic adjustment rule should be annual.

Whether the updating of the rule is made at long intervals, there could raise not only financial problems but also intergenerational iniquities. Clearly, whether the life expectancy of people belonging to the first cohort of the interval is enforced to the remaining cohorts, a deficit should occur and, additionally, the actuarial fairness should be infringed. Surely, the lack of enforcing the automatic adjustment rule is the main issue which could undermine the financial viability of NDC. When policymakers deny their pre-commitments, then financial feasibility and credibility will be broken. At the theoretical level, the political feasibility relies simply on the assumption that the automatic adjustment rule is enforced by law. However, this assumption is not a sufficient condition to avoid the political risk. Indeed, political feasibility does not follow automatically when institutional links for maintaining the political pre-commitments do not exist.

Conclusion

This paper attempted to deal with some open issues raised in the literature on the differences of both NDC and DB and their capabilities to deal with the ageing of population. The main findings are the following.

First, by developing a framework where longevity is introduced – so that the retirement age constitutes an additional instrument variable in the pension plan for counterbalancing economic and demographic shocks – we showed that the two pension systems share the same properties and perform the same outcome.

Secondly, we have pointed out that the need to enforced balance constraint modifies the priorities of a pension plan and requires renouncing to the goal of individual well-being in both pension systems.

Thirdly, by developing Musgrave’s suggestion on the alternative pension policies about risk-sharing among generations, we have showed that when longevity is taken explicitly into account a new pension policy based on an endogenous retirement age can be devised. Indeed, implementing this pension policy could result in significant advantages in an era of population ageing. Actually, it can keep the population structure unchanged by increasing the retirement age. As a result, current workers bear the costs of demographic risks in term of a longer work phase. Notably, a similar pension policy could fulfill not only the requirement of financial solvency but also the traditional goal of a pension system i.e., individual well-being both for current workers and especially for retirees.

References

1. Aaron, H. (1966). The social insurance paradox. Canadian Journal of Economics, 32(1), 371-374.
2. American Academy of Actuaries. (2007). Social security reform options. Public policy monograph. Retrieved from http://www.actuary.org/pdf/socialsecurity/reform
3. Barr, N. (2004). Notional defined contribution pensions: what they can do and what they can’t. Nordisk forsikringstidsskrift, 3(1), 203-214.
4. Barr, N. (2004). Pensions: Challenges and choices: What next? Pensions: Challenges and choices: The first report of the pension’s commission. London, TSO.
5. Barr, N. (2006). Non-financial defined contribution pensions: Mapping the terrain. In R. Holzmann & E. Palmer (Eds.), Pension reform: Issues and prospects for nonfinancial defined contribution (NDC) schemes Pp. 57-69. Washington D.C., World Bank.
6. Barr, N. (2006). Pensions: Overview of the issues. Oxford Review of Economic Policy, 22(1), 1-14.
7. Börsch-Supan, A. (2005). From traditional DB to notional DC systems: the pension reform process in Sweden, Italy and Germany. Journal of the European Economics Association, 3(1), 458-465.
8. Börsch-Supan, A. (2006). What are NDC pension systems? What do they bring to reform strategies? In R. Holzmann & E. Palmer (Eds.), Pension reform: Issues and prospects for non-financial defined contribution (NDC) schemes.
9. Cichon, M. (1999). Nominal contributing schemes: Old wine in new bottles? Internationale Revue für Soziale Sicherheit, 52(4), 105-126.
10. Cichon, M. (1999). Notional defined‐contribution schemes: Old wine in new bottles? International Social Security Review, 52(4), 87-105.
11. Cremer, H., Lozachmeur, J.M., & Pestieau, P. (2006). Social security, variable retirement age and optimal income taxation. Journal of Public Economics, 88(1), 2259-2281.
12. Diamond, P. (1965). National debt in a neoclassical growth model. American Economic Review, 55(1), 1126-1150.
13. Diamond, P. (1996). Insulation of pensions from political risk. In Valdes S (Eds.), The economics of pensions: principles, policies, and international experience. Cambridge: Cambridge University Press.
14. Diamond, P. (2005). Pensions for an ageing population. NBER Working Papers 11877, National Bureau of Economic Research, Inc. Cambridge Massachussetts.
15. Diamond, P. (2005). Saving social security. Journal of Economics Literature, 19(1), 11-32.
16. Diamond, P. (2005). Social security rules that vary with age. In E. Fornero, & P. Sestito, (Eds.), Pension system. Beyond mandatory retirement. Cheltenham: Edward Elgar.
17. Diamond, P., & Orszag, P.R. (2004). Saving social security. A balanced approach. Brookings Institution Press, Washington, DC.
18. Kruse, A., & Palmer, E. (2006). The new Swedish pension system: Financial stability and the central government budget. Paper presented at An International Conference on Social Security Reform in Selected OECD Countries, Urban Institute’s.
19. Liebman, J., MacGuineas, M., & Samwick, A. (2005). Nonpartisan social security reform plan. Retrieved from http://www.nonpartisanssplan.com/pages/1/index.htm
20. Lindbeck, A., & Persson, M. (2006). The gains from pension reforms. Journal of Economic Literature, 41(1), 74-112.
21. Magnani, R. (2016). Is an increase in the minimum retirement age always desirable? The case of Notional defined contribution system. Metroeconomica. International Review of Economics, 67(1), 578-602.
22. Musgrave, R.A. (1981). The reappraisal of financing social security. In F. Skidmore (Eds.), Social security financing. Cambridge, MA: MIT Press.
23. Palmer, E. (2000). The Swedish pension reform: Framework and issues. Pension Reform Primer, Social Protection Paper 0012, the World Bank, Washington DC.
24. Pestieau, P. (2003). Raising the age of retirement to ensure a better retirement. The Geneva Papers on Risk and Insurance. Issues and Practice, 28(4), 686-695.
25. Pestieau, P., Ponthiere, G., & Sato, M. (2006). Longevity and pay-as-you-go pensions. CORE discussion paper 2006/54.
26. Poole, W. (2004). Social security reform and demographic reality. Retrievd from http://stlouisfed.org/news/speeches/2004/10_19_04.html
27. Samuelson, P.A. (1958). An exact consumption-loan model of interest with or without the social contrivance of money. Journal of Political Economy, 66(6), 467-482.
28. Settergren, O., & Mikula, D. (2001). The automatic balance mechanism of the Swedish pension system. Wirtschaftspolitische Blätter, 4(1), 1-9.
29. World Bank. (2001). National accounts. National defined contribution plans as a pension reform strategy. World Bank pension reform primer.