Research Article: 2021 Vol: 25 Issue: 3
Modelling Dual-Sourcing of Product Returns Collection with Surge In Returns Quantity
Siddhartha Kushwaha, Goa Institute of Management
Abstract
The seasonal online sales result in a surge in product returns following the sales. The study presents a mixed-integer linear programming model for a manufacturer, to select collection outsourcing policy under surge supply of product returns. There are two streams of product returns i) regular returns at the end of the service life of the product, and ii) surge returns in the period due to discount sales during the holiday. The manufacturer has a dual source of collection activity i) independent collection firms (ICF) in each locality where the company is marketing new products and ii) collecting product returns in-house centrally
Keywords
Product Returns Collection, Outsourcing Strategy, Dual Sourcing, Surge Supply, Seasonal Marketing, Online Marketing, Mixed-Integer-Linear Programming.
Introduction
The surge in return of products is a cost to manufacturers. There are several reasons for the surge in product returns. Few common reasons for this surge in product returns are primarily an outcome of product promotion and sales push to customers, which includes the return of additional products received by customers as gifts during festivals, easy shopping of products in reply to seasonal online product discount sales. The quantum of surge return problem has been observed in several instances. In the USA, a total of $ 280 million worth of products are returned to retailers after the 2014 charismas season1 which increased to the inventory of worth $90 to 95 billion2, and as many as 40% of online sales of apparel result in return post an online sales program3. The source of a surge in product returns depends on the cause of returns and can be either focused at a locality or spread across a new product market. This paper specifically focuses on the problem of channel selection formulation for the surge in product return occurrence at distributed geographic locations.
Literature Review
Past literature on the collection of used products has extensively explored the outsourcing policy-making by a manufacturer for reverse supply chain through retailers (Savaskan & Wassenhove, 2006), through retailer and third party firm(s) (Savaskan et al., 2004; Huang et al., 2013; Hong et al. (2013); Ma et al. 2016). Earlier researchers also consider stochastic demand for a new product (Xanthopoulos et al., 2011; Chuang et al, 2014). Available studies focus on the variable cost of used products collection activity in a single period context (Savaskan et al 2004, 2006, Huang et al. 2013; Hong et al., 2013; Chuang et al. 2014; Ma et al. 2016).
In forward supply chain, a dual supply chain for handling surge is suggested by researchers (Allon, & Van Mieghem, 2010), (Janakiraman et al., 2015), (Xin & Goldberg 2017). One channel is for regular supply at a lower transfer price and the second channel for express/emergency supply at a shorter lead-time but higher transfer price. A reverse supply chain, which has a dual supply channel of used products, may sustain a surge in returns supply.
We study a problem context with some potential independent collection firms (ICFs) are available at various localities to a manufacturer for the collection of product returns. These ICFs collect product returns at asymmetric transfer prices.
The asymmetry in transfer price is a reflection of the quantity they may collect in their locality. The manufacturer may select a few of these ICFs for collection from respective localities and collect in-house for remaining localities. The company is responsible for the collection of the quantity of product returns covered under warranty or product return agreement offered with new products. The customers of the products return products in multiple periods. Under these conditions, a manufacturer optimally selects dual sources i.e., ICFs and an in-house collection facility for performing the collection of product returns for minimizing costs.
Model
This section presents the decision-making model. We start the section by describing the notations and assumption for the decision problem context.
Assumptions and Notations
We give a multi-period mixed-integer linear programming (MILP) model, for the dual collection-channel problem of a manufacturer under surge supply of product returns. The company has a dual source of collection activity i) independent collection firms (ICF) in each locality where the company is marketing new products and ii) collecting product returns in- house centrally.
We make the following assumptions:
1. All the remanufactured products are marketed and sold in the same period.(Srivastava & Srivastava, 2006; Mitra, 2007 and Ordoobadi, 2009).
2. Customers return products in two cases- i) regular returns after the product complete its service life and ii) surge return of products purchased by customers during seasonal/discount/special sales push by the marketing department of the company.
3. The company can estimate the quantity of product return for each locality and for the complete planning horizon.
4. The selection of independent collection firms (ICFs) is for the planning horizon. (Ovchinnikov et al., 2014)
5. Customers who are likely to return products to a potential collection center, which is not open, return the products to the manufacturer.
6. The company has a central facility for reverse supply chain activities, which may act as a channel for receiving the product returns from a locality not having a selected ICF. (Savaskan et al., 2004; Ordoobadi, 2009; Atasu et al., 2013 and Ovchinnikov et al., 2014).
7. The company is selecting ICFs for collection activity only. The company will use a central facility for the recovery and remarketing of remanufactured products. Hence, the objective of the manufacturer is minimizing cost as the revenue is fixed.
We give the notations used for the Model in Annexure 1.
Decision Model & Solution Approach
From Assumption 7, the total cost product returns collection is a function of fixed cost (����0) and discounted total variable cost for in-house collection of product returns by manufacturer, and the discounted total transfer price paid to select ICF(s). The discounted cost’s function is the objective function for the planning horizon, is:
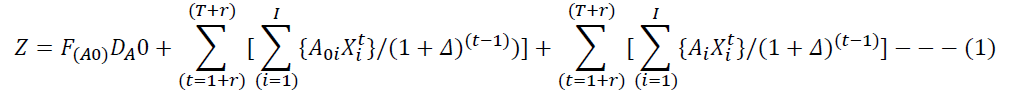
In RHS of the objective function (1), the first term is the fixed cost incurred by the company and the second term is the variable cost incurred for used product collection by the manufacturer and independent collection firms.
A similar formulation is available in the literature (Kushwaha, 2016).
Next, a description of the constraint to which objective function (1) is subjected, is given. These constraints ensure that the assumptions made are followed. From Assumption 2, The product returns from customer due to end of service life or regular returns is αpt-1. The quantity of surge product returns is 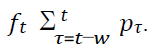 Hence the Constraint (2) ensures that all available
product returns (regular and surge) are received by the company and the ICFs.
Hence the Constraint (2) ensures that all available
product returns (regular and surge) are received by the company and the ICFs.
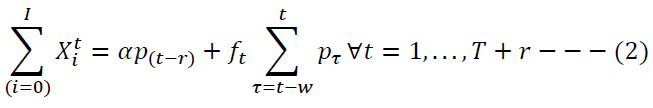
From Assumption 3 and 4, an estimate of product return to an ICF in a locality is a function of regular return in the locality, probable surge quantity of products under warranty, and return the agreement in locality causing surge supply of returns in the current period, and probable surge quantity of products that returned in a historical period. Constraint (3) ensures that only on selection an ICF receives the estimated number of product returns. The quantity of product returns received by the manufacturer from a locality in absence of ICF is given by constraint (4).
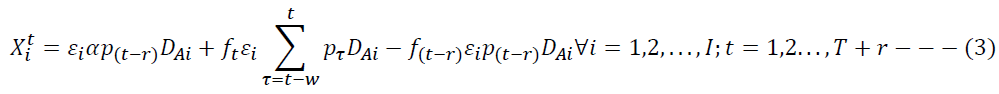
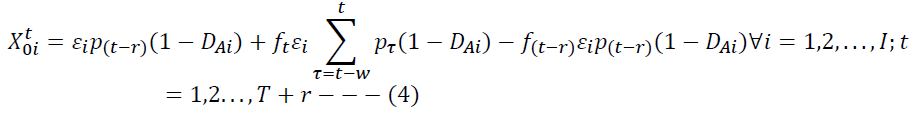
For Assumptions 5 and 6, we formulate the constraint as a fixed charge problem. Constraint (5) implies that the manufacturer engages in collection activity only if the manufacturer receives the product returns from the locality and not selects the ICF for at least one of the localities.
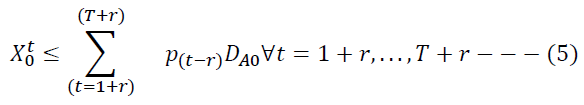
Constraint (6) enforces the non-negativity of decision variables. Constraint (7) imposes a binary constraint on the decision variable for selection and authorization of ICF.
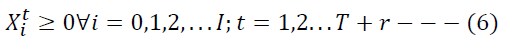
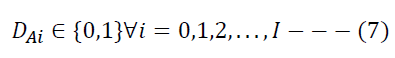
We minimize the cost function Z subjected to constraints (2) to (7) to obtain a suggested outsourcing policy for the manufacturer.
The model is Mixed Integer Linear Programming (MILP) formulation. The branch and bound algorithm available in the software LINDO and GAMS could be used to arrive at a solution.
Literature review and field studies are to be used to estimate the parameter values. A manufacturer can use the sensitivity analysis to study the sensitivity of the solution to changes in the parameter values to formulate a dual-sourcing policy for collection activity.
Conclusion
The study has two central contributions- i) a novel multi-period collection activity outsourcing decision model for manufacturers that consider surge supply of product returns, ii) extensions of the formulation may be used to develop mathematical models for recovery activity outsourcing policies.
Annexure 1: Notations
Indices
i : Index of potential firm for collection of used products, = 1... I
t : Index of time period, = 1...T
s : Index of subassembly in the product, = 1...S
Parameters
r : Lead time between sales and return of products, assumed constant
w : Duration for which Warranty and return agreement is valid
pt : Quantity of new products produced by manufacturer in period t,t = 1, 2... T,
α : Fraction of new products produced in time period t which are returned in period t+r; t=1, 2...T.
f: Probability of surge in the period t , Please note we are assuming ft=1 if surge happen and = 0 if not.
FA0: Fixed cost incurred by manufacturer for engaging in collection of used products at the beginning of the planning period.
A0i: Per unit variable cost of e-waste collection incurred by manufacturer from ICF i
A : Per unit variable cost paid by manufacturer to authorized ICF i for collecting product returns and supplying to manufacturer, i = 1,2,... I
ε : Estimated fraction of total product returns likely to be received by potential ICF i, i = 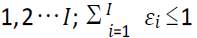
Δ: Rate of discount for calculating discounted cost.
Decision Variables
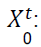 Quantity of used products received by the manufacturer in the period t. For single period
context t=1.For multi-period context t = 1+r, 2+r…T+r.
Quantity of used products received by the manufacturer in the period t. For single period
context t=1.For multi-period context t = 1+r, 2+r…T+r.
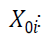 Quantity of used products received by the manufacturer directly from consumer in
vicinity of ICF i in the period t. For single period context t=1.For multi-period context t = 1+r, 2+r…T+r.
Quantity of used products received by the manufacturer directly from consumer in
vicinity of ICF i in the period t. For single period context t=1.For multi-period context t = 1+r, 2+r…T+r.
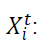 Estimated quantity of used product returns at potential ICF i in the period t. For single
period context t=1.For multi-period context t = 1+r, 2+r…T+r.
Estimated quantity of used product returns at potential ICF i in the period t. For single
period context t=1.For multi-period context t = 1+r, 2+r…T+r.
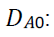 A binary variable
A binary variable
= 1 if manufacturer is engaged in collection of used products
= 0, otherwise
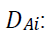 Binary variables, i = 1,2, ... I
Binary variables, i = 1,2, ... I
= 1 if a potential ICF i is selected and authorised for used product collection
= 0, otherwise
End Notes
1https://news.utdallas.edu/business-management/researchers-examine-effect-of-return-policies-on-c/
2https://www.cnbc.com/2019/01/10/growing-online-sales-means-more-returns-and-trash-for-landfills.html
3https://www.thehindubusinessline.com/companies/free-returns-a-way-to-lure-customers-to-do-online-shopping/article32069191.ece
References
- Allon, G., & J.A. Van Mieghem. (2010). Global Dual Sourcing: Tailored Base-Surge Allocation to Near- and O_shore Production. Management Science 56 (1): 110-124.
- Atasu, A., Toktay, L.B., & Van Wassenhove, L.N. (2013). How Collection Cost Structure Drives a Manufacturer’s Reverse Channel Choice. Production and Operations Management, 22(5), 1089-1102
- Chuang C, Wang CX, Zhao Y. (2014). Closed-loop supply chain models for a high-tech product under alternative reverse channel and collection cost structures. Int J Production Economics; 156:108-123.
- Hong X, Wang Z, Wang D, Zhang H. (2013) Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection. Int J Adv Manuf Technol;68:1851-165.
- Huang M, Song M, Hay L, Ki W. (2013) Analysis for strategy of closed-loop supply chain with dual recycling channel. Intern J Prod Econ; 144:510–520.
- Janakiraman, G., Seshadri, A. Sheopuri (2015). Analysis of tailored base-surge policies in dual sourcing inventory systems. Management Sci. (61): 1547-1561.
- Kushwaha, S. (2016). Outsourcing Strategy of E-waste collection activity for a Manufacturer. Management & Labour Studies. 41(1): 58-62.
- Kushwaha, S. & Bhattacharya, S. (2015). Impact of cannibalization on product return under different demand scenarios.IUP Journal of Operations Management. 14(1), pp. 39-53.
- Ma Z, Zhang N, Dai Y, Hu S. (2016). Managing channel pro fi ts of different cooperative models in closed-loop supply chains. Omega; 59:251–62.
- Martin, P., Guide Jr., V.D.R., & Craighead, C.W. (2010a). Supply Chain Sourcing in Remanufacturing Operations: An Empirical Investigation of Remake Versus Buy. Decision Sciences, 41(2), 301–324.
- Mitra, S. (2007) Revenue management for remanufactured products. Omega, 35(5), 553–562.
- Ordoobadi, S.M. (2009). Outsourcing reverse logistics and remanufacturing functions: a conceptual strategic model. Management Research News, 32(9), 831–845.
- Ovchinnikov, A., Chao, & Xiang. (2014). Remanufacturing Strategies for OEMs without Remanufacturing Capabilities. Production and Operations Management.
- Samsung (n.d.) Samsung take back and recycling program, retriveed November 22, 2014 from http://www.samsung.com/in/samsungrecycle/
- Savaskan, R.C., Bhattacharya, S., & Van Wassenhove, L.N. (2004). Closed-Loop Supply Chain Models with Product Remanufacturing. Management Science, 50(2), 239–252.
- Savaskan R.C, Van Wassenhove L.N. (2006). Reverse Channel Design: The Case of Competing Retailers. Management Science; 52:1–14.
- Srivastava, S.K., & Srivastava, R.K. (2006). Managing product returns for reverse logistics. International Journal of Physical Distribution & Logistics Management, 36(7), 524–546.
- Xanthopoulos A, Vlachos D, Iakovou E. (2012). Optimal newsvendor policies for dual- sourcing supply chains: A disruption risk management framework. Comput Oper Res; 39:350–3507.
- Xin, L., D.A. Goldberg. (2017). Asymptotic optimality of tailored base-surge policies in dual- sourcing inventory systems. Management Science, 64(1),437-452.