Keywords

Innovative development; Economy development; Social development; Ecological development; Information economy.

Introduction

According to the paradigm of sustainable development, the main goal is not to increase economic power of economic entities, but to ensure high economic results through careful and efficient use of resources without harming future generations, taking into account social orientation of increasing economic power. At the same time, the development of economic systems at any level is possible only under the conditions of innovation direction. Under such conditions of the world economy development, innovations do not serve as an end in themselves, but are a tool to stimulate the growth of economic, social and environmental development. This and other things require the development of methodological tools for assessing the impact of innovation on the economic systems development in accordance with the components of sustainable development. It should be noted that most methods of determining the impact of innovation factors on the development of regional economic systems are based on the static state of regional economic systems, and dynamic changes are determined by changing the system’s state over time.

The purpose of this study is to develop methodological tools for modeling the impact of innovative factors on economic, social and environmental development of regions.

The scientific novelty of the presented research is that the authors proposed the use of the nonlinear dynamics model to determine the impact of innovation factors on economic, social and environmental development of regional economic systems, which allows to determine the impact of the development functions of regional economic systems in dynamics and to visualize the results in the form of attractors.

Literature Review

Many scientific works of domestic and foreign scientists are devoted to the study of innovation activity and digitalization, as well as innovative factors influencing sustainable development, among them are: Wu J. (2019); Tajpour M. (2020); Ahn J., (2021); Chen M. (2021); Hosseini E. (2021), Hysa E. (2020); Dergaliuk B. (2021); Liu X. (2021); Mhlanga D. (2021); Ravazzoli E. (2021); Revk? A. (2020); Seddon A. (2021); and Vovk O. (2021).

Within the study (Mhlanga D. et al., 2021), author noted that governments of developing countries should invest more in the use of artificial intelligence to achieve the Sustainable Development Goals of innovation, infrastructure development and poverty reduction. Researchers (Ahn J. et al., 2021) have studied the city's innovative projects aimed at the balanced national development of South Korea. In the study, researchers (Chen M. et al., 2021) conclude that despite numerous studies of energy efficiency and innovation in the context of Industry 4.0, little is known about how the degree of economic leakage may affect the association of energy efficiency and innovation. The paper (Ravazzoli E. et al., 2021) aims to fill the gap and assess various aspects of the impact of social innovations on marginalized European and Mediterranean territories. Within the article (Liu X. et al., 2020), the development of the regional economy through technological innovation is studied.

The study (Hysa E. et al., 2020) examines the relationship between individual indicators of circular economy, including the main components of environmental and economic growth. Based on the data of the provincial committee, the article of the Chinese scientist (Wu J., 2019) empirically aims to study the impact of technological innovations on environmental pollution and considers the moderating role of the Internet development in this sphere. According to (Seddon A., 2021), environmental sustainability has become a key concept in ecosystem management. Paleoecological records are useful archives for addressing ecological sustainability, as they can be used to reconstruct long-term temporary changes in ecosystem properties.

Materials and Methods

The nonlinear dynamics model to determine the impact of innovation factors on the development of regional economic systems can be represented in general terms through changes in certain parameters of economic development. In general, the function of the influence of innovative factors using Equation 1.

Where:

the first periodic linear function has four characteristics, namely:

a - amplitude characteristic of the control of the periodic function;

b - frequency response of the control of the periodic function;

c - phase characteristic of the control of the periodic function;

d - offset characteristic of the function. the second linear function changes under the influence of other four characteristics, namely:

e - amplitude characteristic of the linear function;

i - time (in our case, a period from 2013 to 2020);

g -the characteristic of the displacement of the linear function;

h - the characteristic of the transfer of a linear function. the third function, as already mentioned, is also linear, where:

j - amplitude characteristic of the linear function;

i - time (years);

k - the characteristic of the displacement of the linear function;

l - the characteristic of the transfer of a linear function. in the fourth quadratic function:

r - amplitude characteristic of the quadratic function;

m - amplitude characteristic of the displacement of the quadratic function;

s - transfer characteristic of the quadratic function.

We can see that the presented Eq. 1 has four functions, of which the first three functions are linear and the last is quadratic.

It should be noted that amplitude characteristic is a change in the value of the functions, offset characteristic is a change in the horizontal axis, and transfer characteristic is a change in the vertical axis. According to our study, to determine the impact of innovation factors on the development of regional economic systems, the Eq. 1 will look like Equation 2.

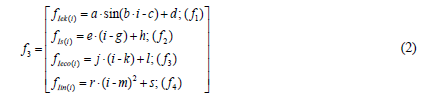
The function represented by Eq. 2 is based on the dependences of variable regional economic systems, which form corresponding indices of the components of sustainable development (??k, ?s, ??co, ?in). This, in turn, makes it possible to identify the relationships that will be included in the nonlinear dynamics system to determine the impact of innovation factors on the development of regional economic systems, using Eqs. 3, 4 and 5.

Firstly,

Secondly

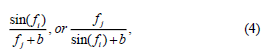
Thirdly,

Where; α - amplitude characteristic of the group of functions;

k - offset characteristic of the group of functions.

On the basis of the three given relations we will construct a variant of the model of components of the development of regional economic systems through economic, social and ecological components of the development in the form of the functions entering into the system of Eqs. 6 to 9.

f1 - index function of the component of economic development of the regional system.

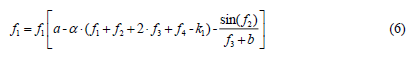
f2 - index function of the component of social development of the regional system:

f3 - index function of the component of ecological development of the regional system:

f4 - index function of the component of innovative development of the regional system:

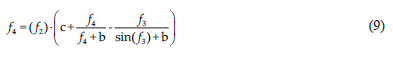
Taking into consideration these functions, the model of the equations system for determining the impact of innovative factors on economic, social and environmental development of regional economic systems based on functional dependencies of regional indicators and indices of economic, social, environmental development using Equation 10.

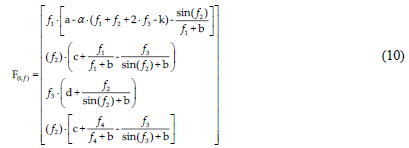
Where: α - amplitude characteristic of the group of functions;

k - offset characteristic of the group of functions;

a - amplitude characteristic of the control of the periodic function;

b - frequency response characteristic of the periodic function;

c - phase control parameter of the periodic function;

d - characteristic of the offset function.

f1 -index function of the component of economic development of the regional system;

f2 - index function of the component of social development of the regional system;

f3 - index function of the component of ecological development of the regional system;

f4 - index function of innovation development.

We came to conclusion that application of the nonlinear dynamics model makes it possible to determine the impact of innovative factors on economic, social and environmental development of regional economic systems, which corresponds to the paradigm of sustainable development.

Results

In order to eliminate one of the disadvantages of using the nonlinear dynamics model, namely the ability to obtain many solutions when applying the approximation of functions and obtaining bifurcation discontinuities when constructing attractors, the authors used the MathCad- 15 software package for calculations. Its use made it possible to apply the 4th order Runge-Kutta method, which minimizes the error in the calculations.

Based on the results of calculations of the application of the nonlinear dynamics model to determine the impact of innovative factors on the development of regional economic systems, we build attractors by solving the differential equations system. The model is based both on certain indicators, and on integrated indices. Integral indices make it possible to cover a large number of heterogeneous parametric characteristics to determine the impact of innovation factors on economic, social and environmental development of regional economic systems.

To determine the impact of innovation factors on the sustainable development of regional economic systems, the authors chose Kiev region, which occupies a leading position in terms of the values of integrated indices of economic, social and environmental development. In Table 1, the data used to calculate the nonlinear dynamics model and the construction of attractors are presented.

Table 1.Significance for the Model of Determining the Impact  of Innovation Factors for Kiev Region, 2013-2020
Indicator	2013	2014	2015	2016	2017	2018	2019	2020	The average value for 2013-2020
Kyiv region
Integral index of the component of economic development (Iek)	0,869	0,775	0,936	0,855	0,721	0,768	0,923	0,990	0,855
Integral index of the component of social development (Is)	0,107	0,338	0,341	0,288	0,488	0,224	0,188	0,333	0,286
Integral index of the component of ecological development (Ieco)	0,602	0,662	0,525	0,516	0,516	0,560	0,653	0,732	0,596
Integral index of innovative development support (Iin)	0,366	0,377	0,355	0,339	0,344	0,366	0,410	0,443	0,375

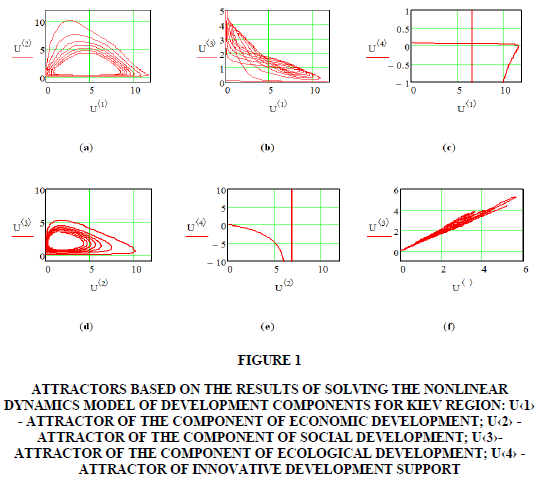
The calculated attractors according to the solution of the nonlinear dynamics model for determining the influence of innovative factors on the development of Kyiv region, which was carried out using the MathCad-15 package based on the solution of the differential equations system with Runge-Kutta solutions of the 4th order, are shown in Figure 1.

In Figure 1, the calculated attractors, dependences between the functions of the components of economic (U^‹1›), social (U^‹2›), ecological (U^‹3›) and innovative (U^‹4›) development are presented, the temporal axis shows the temporal lag, i.e years. The construction of attractors makes it possible to visualize the obtained solutions of the nonlinear dynamics model. If the interaction of economic, social, environmental and innovation components of the development of regional economic systems is the most positive, the attractor is a closed cycle in a certain period of time. This characterizes the stabilizer point of the attractor, which arises from the variant set of phase trajectories obtained as a result of model solutions. The obtained solutions of the nonlinear dynamics model to determine the impact of innovative factors on the sustainable development of Kiev region and their visualization in the form of attractors allow us to note that their illustration shows that not all attractors have closed trajectories. Since the solutions were obtained using the 4th order Runge-Kutta method, this ensures a high degree of calculation accuracy. The obtained results showed that the function of innovative development support has a bifurcation trajectory of attractors, which indicates the instability and fluctuations of the function. The function of innovative support for the development of Kiev region does not have sustainable development, which is confirmed by visual breaks of the attractor and its bifurcation trajectory. Found attractors makes it possible to state that ensuring the sustainability of the development of Kiev region depends on the innovation function, which is determined by the entry of attractors of economic, social and environmental development in the stabilization regime. The smallest correlation of the impact of the obtained calculations between the innovation components is observed in relation to the environmental component of the development of Kiev region. The most innovative impact is observed on the economic component of development.

Conclusions

Calculations of the differential equations system are based on the integrated indices of innovation, environmental, as well as economic and social development of the regions, which were calculated by the authors specifically for this model. The obtained parameters of dynamic changes make it possible to establish the rate of change of the studied functions of the development of regional economic systems and to identify the most optimal parameters for managing the development of regions.

In addition, the application of the nonlinear dynamics model to determine the impact of innovation factors on the development of regional economic systems is of great practical importance, as it provides high accuracy of proof of statistical methods for solving the characteristics of systems. This is important because regional economic systems are complex, dynamic systems with many processes and heterogeneous causal relationships. The construction of attractors makes it possible to show with the greatest accuracy the sustainability of regions under the influence of innovative development factors.

Further research requires applied mechanisms to intensify innovation processes in regional economic systems and to develop a methodological approach to determine the effectiveness of management decisions in this area.

References

1. Ahn, J., Seo, D., & Kwon, Y. (2021). Impact of innovation city projects on the national balanced development in South Korea: Identifying regional network and centrality. ISPRS International Journal of Geo-Information, 10(3), 169.
2. Chen, M., Sinha, A., Hu, K., Shah, M. I. (2021). Impact of technological innovation on energy efficiency in the Industry 4.0 era: Moderation of shadow economy in sustainable development. Technological Forecasting and Social Change, 164, 120521.
3. Hysa, E., Kruja, A., Rehman, N. U., & Laurenti, R. (2020). Circular economy innovation and environmental sustainability impact on economic growth: An integrated model for sustainable development. Sustainability, 12(12), 4831.
4. Liu, X., & Chen, Z. (2021). Research on the Impact of Technological Innovation on Regional Economic Development Under the Background of Internet. In International Conference on Cyber Security Intelligence and Analytics (??. 320-326).
5. Mhlanga, D. (2021). Artificial intelligence in the 4.0 industry and its impact on poverty, innovation, infrastructure development, and sustainable development goals: Lessons from emerging economies? Sustainability, 13(11), 5788.
6. Popelo, O., Tulchynska, S., Kharchenko, Y., Dergaliuk, B., Khanin, S., & Tkachenko, T. (2021). Systemic Approach to Assessing Sustainable Development of Regions. Journal of Environmental Management and Tourism, 3(51), 742-753.
7. Ravazzoli, E., Dalla Torre, C., Da Re, R., Marini Govigli, V., Secco, L., Górriz-Mifsud, E., … & Nijnik, M. (2021). Can social innovation make a change in European and Mediterranean marginalized areas? Assessment of social innovation impact in agriculture, fisheries, forestry, and rural sustainable development. Sustainability, 13(4), 1823.
8. Revko, A., Butko, M., & Popelo, O. (2020). Methodology for Assessing the Influence of Cultural Infrastructure on Regional Development in Poland and Ukraine. Comparative economic research: Central and Eastern Europe, 23(2), 21-39.
9. Seddon, A. W. R. (2021). Special feature: measuring components of ecological resilience in long-term ecological datasets: Palaeoecology and ecological resilience. Biology Letters, 17(1), rsbl20200881.
10. Tajpour, M., & Hosseini, E. (2021). Entrepreneurial Intention and the Performance of Digital Startups: The Mediating Role of Social Media. Journal of Content, Community & Communication, 13, 2-15.
11. Tajpour, M., Hosseini, E., & Salamzadeh, A. (2020). The effect of innovation components on organisational performance: case of the governorate of Golestan Province. International Journal of Public Sector Performance Management, 6(6), 817-830.
12. Vovk, O., Kravchenko, M., Popelo, O., Tulchynska, S., & Derhaliuk, M. (2021).  Modeling the Choice of the Innovation and Investment Strategy for the Implementation of Modernization Potential. WSEAS Transactions on Systems and Control, 16, 430-438.
13. Wu, J. (2019). Research on the Impact of Technological Innovation on Environmental Pollution - Based on the Moderating Effect of Internet Development. Proceedings of 2nd International Symposium on Architecture Research Frontiers and Ecological Environment, 143, 02054.