Keywords

Location, Supply Chain, Multi-Product, Distribution, Multi-Period.

Introduction

In general, positioning is an activity that evaluates and analyzes the potential and actual talents of an area in order to choose a suitable location with specific goals such as minimizing transportation costs, providing equal facilities for customers, and obtaining the most market share. and is related to broad research fields such as research in operations, management sciences, industrial engineering, geography, economics, engineering sciences, mathematics, marketing, urban planning. Location of warehouses, factories, hospitals and wholesalers can be mentioned as examples of classic applications of this field. Among other applications, we can mention the location of power plants and components of electricity production and distribution systems, factory warning systems, water supply systems in agriculture, exploration and drilling of oil wells.

Choosing the right location for the establishment of facilities is a search to find a place that can be coordinated with the specific needs of the related facilities. The needs related to establishing and choosing the location of the facilities according to the desired criteria are called location. In such a process, the first step is to collect data and information, after determining the positioning criteria. Since positioning requires a lot of real information, a large amount of information to introduce different places must be collected, combined and analyzed in order to make a correct assessment of the factors that may be effective in the selection. In this regard, the location of urban service facilities such as the location of aid stations, police, fire department is a process during which the capacity and capabilities of a specific area, in terms of the presence of suitable and sufficient land and its connection with other urban facilities, in order to choose a suitable place for Specific (applications) are studied and analyzed (Altiparmak, 2006).

Literature Review

In 2018, a research conducted by Atiyeh Ghorbani and his colleagues on location-routing-inventory problems, which is a three-level supply chain including suppliers, warehouses, and customers, and is considered for multi-product and multi-period problems. and a mixed integer model is presented and the combined algorithm of SA and colonial competition (IC) is used. The results show that the algorithm (IC-SA) is more efficient in terms of the quality of answers and time compared to the SA algorithm.

Eskigun et al. (2018) in their two researches on the topic of designing an output chain network by choosing the mode, waiting time and car distribution centers, discussed the stopping time in the nodes of the structured network model and the effect of waiting time for delivery on They examined the external structure of the supply chain. They showed that in order to achieve the goals, a balance should be achieved between the external structure of the supply chain and the waiting time for the delivery of the product to the customers.

Jian Mai Shi et al. (2019) in a research titled "Presenting the design model of the construction supply chain network based on demand and solving it using the Lagrange release algorithm" presented a solution algorithm based on the Lagrange release algorithm for the BTO chain network design problem. The issue was determining the location of distribution centers and assigning distribution centers or factories to retailers (Narges Nowrozi, 2016).

Statement of the Problem

In this research, a new multi-product and multi-period facility location model is developed in the design of the supply chain distribution department, which is a three-level supply chain including suppliers, retailers, and final customers. The objective function minimizes the total cost, which includes the cost of transportation between central and regional warehouses, the cost of transportation between the regional warehouse and the customer, the cost of establishing central warehouses, and the cost of establishing regional warehouses (Shi, 2012).

The Examined Components are:

• Central Warehouses: Main stocks required from the supply chain are sourced here.

• Regional Warehouses: Demand stocks are distributed between central warehouses and customers here.

• Customers: Customers who are located in provincial cities.

• Goods: goods that can be offered to customers

Mathematical Modeling

The assumptions of the problem are as follows:

• Both central and regional warehouses have limited capacities. The model is considered as multi-product.

• The transportation cost per unit is specified as the distance factor between the central and regional warehouses and between the regional warehouse and the customers.

• The model is considered multi-period.

Collections and Profiles

• L set of central warehouses (|L| = l,k ε L)

• M set of regional warehouses (|M| = m,j ε M)

• N set of customers (|N| = n,i ε N)

• set of types of products (|O| = o,tf ε O)

• F time period

The Main Parameters of the Problem

• aitf customer i's demand for product t in period f,

• bjtf regional warehouse capacity j for product t in period f,

• c transportation cost per product unit,

• dij, the distance between regional warehouse j and customer i,

• d'jk, the distance between regional warehouse j and central warehouse k,

• ektf central warehouse capacity k for product t in period f,

• P coefficient of the total cost in the objective function,

• Qk the cost of establishing a central warehouse k,

• sitf is the minimum satisfaction level of customer i for product t in period f,

• wj the cost of establishing a regional warehouse j.

The Decision Variables of the Problem

• νk = 1, if the potential point k is positioned for central storage, = 0, otherwise,

• uj = 1, if potential point j is designated for regional storage, = 0, otherwise,

• xijtu percentage of customer i's demand for product t in period f, supplied by regional warehouse j,

• yjktu percentage of demand of regional warehouse j for commodity t in period f supplied by central warehouse k.

The Main Research Model

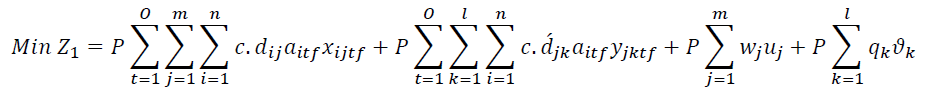
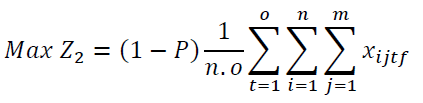
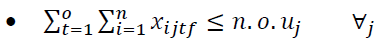
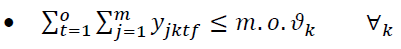
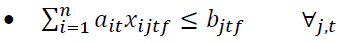
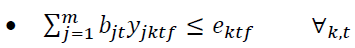
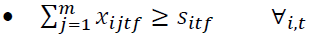
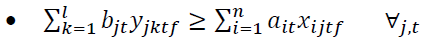
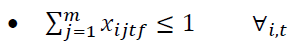
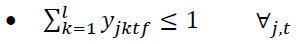
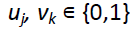
The elements of the objective function are:

• Transportation cost between central and regional warehouses,

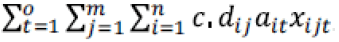
• The cost of transportation between the regional warehouse and the customer,

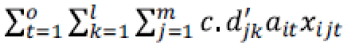
• The cost of establishing central warehouses,

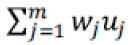
• The cost of establishing regional warehouses,

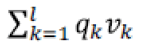
• which is multiplied by the weighting factor P.

Constraints 1 and 2 also state that if the regional warehouse j or the central warehouse k meets the demand, it will be established. Conditions 3 and 4 indicate the capacity limit for each regional warehouse. Condition 5 implies that there is a minimum level of satisfaction of customer i for product t in period f. In condition 6, the amount of supply should be more than the amount of demand. Condition 7 indicates that the maximum level of satisfaction of customer i for product t in period f must be less than or equal to 1. Condition 8 specifies that the percentage of total regional warehouse demand j for product t in period f must be less than or equal to a. In this thesis, GAMS software is used for problems with small dimensions. The cost of establishing regional warehouses, which is multiplied by the weighting factor P.

Evaluation of the Results

In order to further evaluate how to solve the problem in this research and to evaluate the performance of the proposed algorithm, in this part, various problems are designed and solved. Small-scale test problems are solved. These problems are solved with a mathematical model using Gems software and the results are analyzed.

General Assumptions of Algorithms

To show the proper performance of the designed algorithm, several problems have been generated and solved see Table 1.

Table 1 Parameter Range for Testing the Problem
Random function	parameter	Introduction to parameter
(5-15)	aitu	demand of customer i for product tu in period u
(15-50)	bjtu	Regional warehouse capacity j for commodity tu in period u
(5-15)	dij	the distance between regional warehouse j and customer i
(5-15)	d'jk	the distance between regional warehouse j and central warehouse k
(15-50)	ektu	Central warehouse capacity k for item tu in period u
0.5	P	the total cost coefficient in the objective function
(1-10)	qk	cost of creating a central warehouse k
0.1	situ	the minimum satisfaction level of customer i for product tu in period u
(1-10)	wj	the cost of creating a regional warehouse j

The problem is considered with diverse and different conditions. The problems are implemented by the proposed model using GAMS exact solution software. Their results are compared see Table 2.

Table 2 Solution Results
ردیف	Z	ZTU	TUime
1	10611.992	5305.986	23.84
2	12138.52	6069.25	128.6
3	18660.239	9330.109	933.36
4	37305.52	18652.75	2148.35
5	51264.635	25632.31	3600
6	243526.83	121763.4	3600
7	552661.32	276330.6	3600
8	1119801.5	559900.7	3600
9	1784761.5	892380.7	3600
10	2518456.7	1259228	3600

Solution Results

Conclusion

In this research, we presented a new mathematical model. First, the mathematical model was developed. An objective function was considered with cost reduction, as well as constraints, the most important of which were demand satisfaction constraints and capacity constraints.

One of the important points is that the number of input parameters is relatively large, so it has a certain complexity and the results show that the algorithm is executed in a reasonable time and suitable for the designed test problems. In order to ensure the performance of the proposed algorithm, various problems for Testing and performance evaluation of the algorithm has been designed in various dimensions. Then, the optimality of the algorithm was evaluated by comparing its results and the results obtained from solving the mathematical model in problems with small dimensions, which showed that the developed model is acceptable.

References

Altiparmak, F., Gen, M., Lin, L., & Paksoy, T. (2006). A genetic algorithm approach for multi-objective optimization of supply chain networks. Computers & industrial engineering, 51(1), 196-215.

Google Scholar, Cross Ref

Eskigun, E., Uzsoy, R., Preckel, P. V., Beaujon, G., Krishnan, S., & Tew, J. D. (2005). Outbound supply chain network design with mode selection, lead times and capacitated vehicle distribution centers. European Journal of Operational Research, 165(1), 182-206.

Google Scholar, Cross Ref

Narges Nowrozi, Reza Tavakoli Moghadam, Mohsen Sadegh Amal Nik "New mathematical modeling for the problem of location of facilities and routing of vehicles and its solution with the integrated colonial competition algorithm" Journal of Industrial Engineering, University of Tehran, 2016.

Google Scholar

Shi, J., Zhang, G., & Sha, J. (2012). A Lagrangian based solution algorithm for a build-to-order supply chain network design problem. Advances in Engineering Software, 49, 21-28.

Google Scholar, Cross Ref

Received: 28-Apr-2023, Manuscript No. IJE-24-14915; Editor assigned: 01-May-2024, Pre QC No. IJE-24-14915 (PQ); Reviewed: 15-May-2024, QC No. IJE-24-14915; Revised: 20-May-2024, Manuscript No. IJE-24-14915 (R); Published: 27-May-2024