Keywords

Coordinated Decisions, Preferred Decision Trajectory, Organization Development Management, Successful Development of an Organization, Multi-Objective Approach.

Introduction

In strategic management, the balanced scorecard system (BSC) is often used to describe the current state of an organization and its development goals (Norton & Kaplan, 1996). The main idea of this approach is to use a system that includes four groups of indicators:

• Financial indicators;

• Environmental indicators (relationships with customers, partners, subcontractors, the size of the market, the market share in the target segment, etc.);

• Indicators that are related to the internal processes of the company (production, supply, sales, innovations, etc.);

• Indicators that describe the ability of the company to acquire new knowledge and grow (personnel and their skills, abilities and motivation, information systems and organizational procedures of interaction between subjects that establish the decision-making system).

These groups of indicators are formed during the description of the “desired future” of the organization. These indicators (“criteria of success”) are based on forecast information with regard to the available knowledge and ideas of the head of the organization; they describe the current ideas regarding the state of the managed object and the desired image of the future–the development goal.

The categories of these indicators form the “conceptual”, “descriptive” model that describes the main properties of the object and the main connections between these properties. Such models are often rudimentary and inaccurate, but it enables the manager to correlate parts of the whole process of development management and “figure out the situation at a glance”, which is especially important during goal setting.

However, when managing real systems, even a full set of indicators that adequately describe the current state of the system does not solve the problem of development in which the desired state is unachievable due to current limitations. A simple translation of model parameters that characterize effectiveness into variables increases dimensionality significantly and causes nonlinearity that prevents one from using simple models that are easy to interpret. This approach allows obtaining quality results in the conditions of small dimensions (Trenev & Krupenin, 2016).

Studies on the methods of active system modelling contributed greatly to the understanding of the mechanisms of management of complex distributed systems. These models, which are similar to games, model the mechanisms of interaction of distributed system elements during development management processes (Burkov & Dzhavakhadze, 1997; Korepanov & Novikov, 2016; Korgin & Korepanov, 2016; Kharchenko, 2014). However, certain difficulties exist when one attempts to create managerial information technologies that can be used in practice.

On the contrary, methods that are based on the ideology of the program-oriented and objective-oriented approach are easy to interpret; they enable switching to information technologies that can be implemented in practice (Zubarev, Irikov & Korgin, 2012; Kharchenko, 2014; Milner, 2008; Trenev & Irikov, 1998). However, this creates a problem of system development modelling.

The system optimization approach models the methods of management of model parameters (Irikov & Trenev, 1999; Novokov, 2016).

However, the remaining problem is the development of mathematical models of management of complex distributed systems and procedures of formation of acceptable decisions with the possibility of purposefully adjusting the parameters of these models.

The purpose of this study is to formalize the models of development management and to describe the mechanisms of formation of coordinated managerial decisions during the management of complex distributed organizational and technical systems, such as big companies and corporations. The applied (practically significant) goal of the study is to rationalize scientifically the comprehensive approach to the reformation of industrial companies, with a view to ensuring their competitive sustainable functioning.

The combination of the program-oriented and objective-oriented approach with the methods of systems analysis and system optimization enables creating simple models of development management that are easy to interpret. The comparison of the range of achievable values of the model with the “desired image” or “range of target values” (the goal) reveals the problems of development, which largely determines the direction of the search for controlling actions.

Problem Specification

Assume that the space of indicators that describe the essential properties of the organization features a range of desired future states–the “vision”.

One could say that a series of factors (criteria of “success”) emerge, which describe the future “vision” of successful companies. In other words, there exists a simply connected set, the membership wherein corresponds to the “success” of the organization.

It is possible to formulate certain hypotheses and definitions.

H1: There exists a multi-objective space, the categories whereof describe the successfulness of each organization (the “criteria of success” space).

Definition 1: “Successful” development of an organization means the realization of the desired “vision” (desired future image of the organization).

H2: The space of criteria (“criteria of success”) features a simply connected set ?* (the goal of development – the “set of successful states” or the “range of target states”), the membership wherein corresponds with the “success” of the organization.

?* (the desired state of the managed object) can be set as a range or as a discrete set of points, as it is usually done in planning (Trenev & Krupenin, 2016; Irikov & Trenev, 1999). ?* can be determined in different ways, including implicitly – via a certain preference relation or functional optimization:

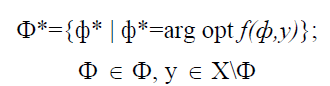
However, at the initial point in the “criteria of success” space, the state of the object is not part of the “range of successful states” area. This “condition of success” is desired, but originally unachievable.

The task of successful development of the organization means the formation of its properties that would allow reaching the “set of successful states”. The achievement of this set can be considered a criterion for the achievement of “success”.

Without losing community, consider that the “criteria of success” space is metric. In this case, the distance from the current state to the boundary of the “set of successful states” (in terms of the chosen metrics) can be considered an indicator of “success” of the organization’s development.

This problem under consideration has certain peculiarities that are related to the specificity of the managed object and the requirements to the procedures of decision formation and making (Trenev & Krupenin, 2016).

The Managed Object is a Complex System

It is impossible to describe the model fully, in detail and adequately at the initial point of work with the object. Our knowledge of the managed object (and the ability to form appropriate and adequate models) is determined in detail and more accurately as managerial problems are solved.

The Managed Object is a Distributed Organizational and Technical System

A big organization, such as an industrial company or corporation, is distributed both spatially and logically. Virtually all real procedures of solution of complex managerial problems include a set of local tasks (such as gathering information, processing information, division of responsibilities for the results, etc.) that are solved iteratively, distributed between various positions (executors) and divided into stages.

• The main peculiarities of a distributed system include the following:

• The existence of a mechanism of system fragmentation into a series of interacting subsystems;

•The existence of a general idea for each subsystem within the framework of the system as a whole;

• Each subsystem functions in isolation and autonomously in accordance with the characteristics of the current (when the decision is chosen) set of possible states, which depend on the states of neighbouring subsystems;

• The existence of a “regulatory factor” that enables isolated executors to form coordinated decisions, with a view to achieving the general goal while performing local tasks within the frameworks of their respective subsystems (this “regulatory factor” should include mechanisms and procedures of coordination and synchronization of subtasks).

It is expedient to give certain definitions, with a view to formalizing the concept of “distributed procedure”.

Definitions:

Managed object: I={i} – managed object I consists of a series of sub-objects {i}, where sequence ?i={?_i,p} describes the state of element i of object I.

Problem:

where ?⁰ is the initial state of the system, ?^* is the finite set of states set on a certain subset 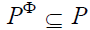of indicators of the system (managed object).

Solution: The P^? set is called the set of outgoing indicators (criteria of the functioning of the system). The state

if 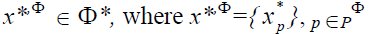i.e. components ?^* that are members of P^? form vector (?^*,?) that lies in the desired range ?^*.

Trajectory: The set of target states ?^* can be set via a trajectory of preferred decisions:

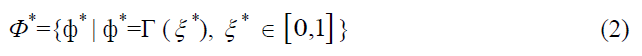
where is a line without loops in space ?, i.e., a trajectory.

In practice, it is impossible to solve the general problem Z₀ without splitting it into specific sub-problems Z_k, for each of which there exists at least one operator A_j,k. that provides its solution:

Here, is a model that corresponds with sub-problem Zk.

Distributed system: A distributed system can be defined as a sequence:

Where, 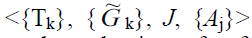is a set of local sub-problems 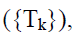models 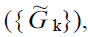executors (J) and mechanisms for forming decision 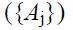that correspond with these subproblems.

Distributed procedure: A sequence

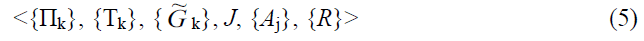
Where R is the “regulatory factor” is called a “distributed procedure”.

In reality, it is necessary not only to find the optimal solution, but also to create a mechanism for the system’s transition from the initial state to the optimal one.

Consequently, the problem consists of three parts: construction of procedures and algorithms for the solution of local problems; construction of a procedure that realizes the “regulatory factor” that leads to a coordinated common decision.

Problem Structuring

Consider an example of a planning procedure for company development options.

Stage 1: Prediction of demand, assessment of changes in the environment, setting of target indicators, determination of the level of required production capacities.

Stage 2: Determination of the necessary and available resources.

Stage 3: Analysis of the gaps between the target results and results that are achievable at the start of works, determination of possible losses.

Stage 4: Determination of the main inhibiting factors (problems and “bottlenecks” of development), formulation of requirements to changes that are necessary to satisfy needs and achieve the desired goals.

Stage 5: Determination of measures for the removal of “bottlenecks” and determination of the main directions of changes.

Stage 6: Analysis of the maximum possibilities (potential of the company) for removing “bottlenecks”. Adjustment of initial goals, if needed.

Stage 7: Compilation of a realizable variant of the program of changes (reforms) and formation of measures for its realization.

The most important aspect is the fifth subclass of problems – innovative management problems (system optimization problems).

Purposefulness of organizational and technical systems, system optimization problems (innovative management problems).

Consider a formalization of system optimization problems (innovative management problems).

The development of an organization (industrial company) requires solving innovative management problems, including the problems of choice of a promising technological structure. These problems are related to the management of scientific and technological progress, since the technological structure determines the specific expenditure of resources and the rational distribution of means that are allocated to the development of the organization under various items of expenditure. Therefore, models of mathematical programming with fixed parameters are insufficient. It is necessary to develop procedures that allow choosing not only the values of unknown variables, but also the parameters of the model, including the elements of the matrix of coefficients and the values of the right-hand side of limitations in conditions when the limitations of the model are inconsistent (the “desired states” range is unachievable until necessary changes are made).

Consider some cases when the goal is presented in the form of a set of desirable values of indicators–in the form of a trajectory development (2).

Innovative management problems (system organization problems)

x-n is the n-dimensional vector of indicators that describe the production capacity of the organization,

?-l is the n-dimensional vector of indicators that describe the output,

?^dir is the vector of target indicators,

D is the l × n matrix that includes the coefficients that determine the effectiveness of the technological structure of the organization

B is the resource vector,

A is the m×n matrix that includes the coefficients that determine the specific expenditure of resources during production,

F_A and F_B are the ranges of possible values of model parameters.

Constraints (6,7) corresponds to the company’s goals of development (“desired” levels of output in the future), constraints (8,9) correspond to the “production capacity” of the company at the start of planning. Condition (10) describes the possibilities of the scientific and technological progress – the possibilities of innovation (possible improvements to the parameters of the technological system). Condition (11) determines the possibilities of redistribution of available resources and the possibilities of mobilization of additional resources.

In general, the production capacity of the organization at the initial point (they are described by constraints (8) and (9)) is insufficient to satisfy long-term needs, which are described by constraints (6) and (7). In other words, the system of constrictions (6)-(9) is incompatible. This contradiction can be removed either by increasing resource supply (increasing B) or via scientific and technological progress, which changes the coefficients of matrix A.

Formulas (10, 11) describe the possibilities of innovative processes.

Range F_A of available values of matrix A elements is found from the following formula:

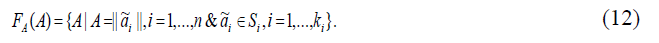
Ranges S_i can be set in various ways:

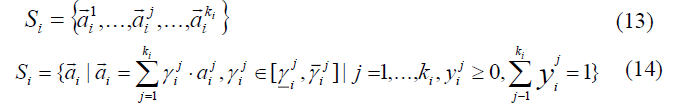
Range F_B of possible values of the right-hand member vector can be set with the following formulas:

The main peculiarity of the problems under consideration is that the goals of development are presented in the form of a trajectory of preferred decisions in the space of output indicators ?_? or in the form of a trajectory in the space of production capacity, ?_x.

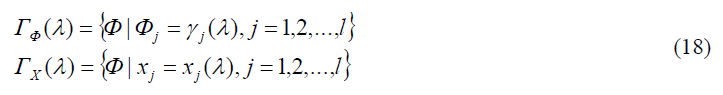
Problem 1.

Value λ determines the possible degree of achievement.

Trajectory ?(λ) is set in the form of a piecewise line without discontinuities and loops with nodes in points s=1, 2, …, m:

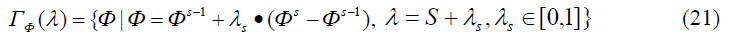
The selection algorithms for the components of vector B and coefficients of matrix A are based on the calculation of the sensitivity coefficients of objective function (19-21) in relation to the components of vector B and matrix A.

The usual methods for solving linear and nonlinear programming problems, which are convenient to use for research purposes, are inconvenient when it comes to practical procedures of planning and management, which impose a series of additional requirements. These requirements are related primarily to the confidence in the adequacy of the obtained results from the point of view of decision makers. In this regard, requirements include the conceptual interpretability of the decision-making procedure steps, regulated degree of automation, the possibility of obtaining a test solution, etc. (Trenev & Krupenin, 2016; Burkov & Dzhavakhadze, 1997).

the future, it will be convenient to use two spaces: the space of output indicators ?, in terms of which the goals of development are formulated and decisions are formed and made and phase space X (space of production capacities), in which resource limitations are set and, in case of resource shortage, parameters A and B are adjusted.

In real procedures of long-term planning and management of development programs, it is possible to form a series of desired values of target indicators: 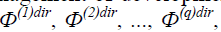which are ordered by the degree of “successfulness”, for instance – “excellent”, “good”, “satisfactory”. The achievement of each “level of success” is determined by the value 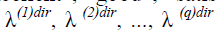of parameter λ, which reflects the degree of achievements of “success” – the movement along the trajectory.

The aggregate of these points forms the trajectory ?(λ) of the most preferred decisions 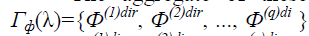n space ? in the form of a piecewise interpolation (21), which is set by points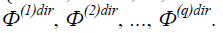

Some properties of such a trajectory (monotony, etc.) enable formulating the problem simply and conveniently: it is necessary to find a decision that lies on the trajectory of preferred decisions and corresponds with the maximally possible value of approximation to the goal λ (Figure 1).

In case of fixed A and B, the decision is located at the intersection of trajectory ? and the boundary of the set of acceptable decisions (Figure 1). In this case, the problem of search for the decision that is closest along trajectory ? to the desired ?^(j)dir formally comes down to a mathematical programming problem (19-21), (6-17).

These peculiarities of the problem (the presence of a “trajectory of the most preferred decisions” and the possibility of simple calculation of sensitivity coefficients, movement along trajectory λ and the degree of resource shortage λ_p depending on B_p and a_pi) enable constructing effective algorithms and procedures of formation of organization development programs (the algorithms are described in Trenev & Irikov, 1998).

Innovative Management Is The Foundation Of The Development Strategy

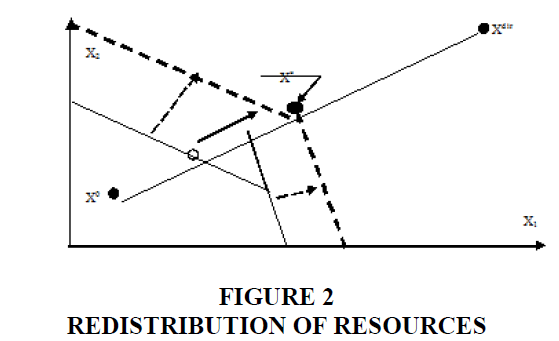
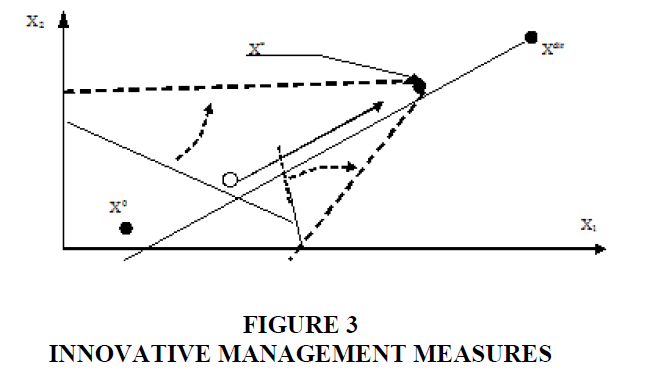
It is possible to move closer to the desired state and expand the range of possible values of the model by adding and reallocating resources (Figure 2). However, the main contribution to the improvement of effectiveness comes from innovative management (Figure 3).

Equations (6-21) give a formal setting of the innovative management problem.

A series of peculiarities of the managed object (organization) allow constructing effective problem solving algorithms and use them to create information technologies that are used in management practice.

These peculiarities include:

• Purposefulness (the presence of a goal in the form of a trajectory of the most preferred decisions);

• Peculiarities of the ranges of possible values of model parameters (set, for instance, by formulas (13-17));

• The possibility to obtain necessary and sufficient conditions of optimality of the solution of the initial problem (6-21).

This, in turn, enables creating information technologies that meet the requirements that are related to the peculiarities of the decision-makers work.

A detailed description of the realization and experience of use of development management procedures that are based on the herein presented results can be found in works (Trenev & Irikov, 1998; Leontiev, Masyutin & Trenev, 2000; Burakov, Burakova & Irikov, 2014; Irikov, Novikov & Trenev, 2009; Ivanov, Trenev & Khalitova, 2015; Leontiev & Trenev, 1997).

Development Management Procedures Based On The Trajectory Approach

Procedure Stages

Stage 1

Goal setting (development trajectory).

• Determination of the initial point of the trajectory.

• Determination of the direction of the trajectory.

• Determination of the degree of movement along the trajectory with regard to limitations.

Stage 2

Determination of development “bottlenecks”.

The maximally achievable degree of movement along the trajectory is determined starting with the top level of the hierarchic model of the organization (in parallel for all the peak of each level). The solution of the problem, i.e. the degree of achievement of the goal, is determined by the peak with the minimum degree of possible movement along the trajectory. This determines the “bottlenecks” in the development of the organization.

Stage 3

“Correction of constraints” (removal of “bottlenecks”).

a) Correction of “upper” constraints of production capacities (increase of 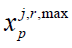in (9));

b) Correction of corresponding coefficients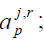

c) Correction of trajectory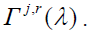

Stage 4

Consolidation of achievements.

Determination of subsystems that achieved maximum development and transition to stage 2 – determination of “bottlenecks”.

The procedure finishes its work if it is impossible to conduct the “correction of constraints” procedure in stage 3 according to the “bottlenecks” discovered in stage 2.

Discussion

The study formulated intuitively obvious hypothesis, based on which it presented mechanisms for setting the target area of development in the form of a trajectory of preferred decisions (2,18,21). This method is easy to understand and customary for managers; it fits well into the information technologies of management.

The approaches that are discussed in section 1 of this paper are sufficiently elaborate, but fragmentary from the perspective of the complex problem of organization development management.

The applied goal of the work, an element whereof is this paper, is to rationalize scientifically the comprehensive approach to the reformation of industrial companies, with a view to ensuring their competitive sustainable functioning.

This implies the accomplishment of the following tasks:

• Investigation of a new class of mathematical models and methods that describe the management of innovations during the reformation of companies (in distributed organizational and technical systems);

• Creation of concrete methods and mechanisms of construction of distributed procedures of formation of coordinated decisions within the distributed system;

• Development of information technologies and specific human-machine procedures for the solution of a series of key problems in the reformation of big industrial companies;

• Development of a software complex for the technical support of strategic decision-making during the reformation of the organization;

• Creation of a complex of engineering methods for managing the development of distributed organizational and technical systems for mass use during the reformation of companies.

The research methods are based on the framework of the theory of management in social and economic systems, the theory of active systems, systems analysis and operation research.

Scientific Novelty of the Study

The theoretical study and generalization of practical experience in the realization of the developed methods and mechanisms resulted in the proposition and practical implementation of a complex approach to the solution of a problem of economic significance – the economic recovery of Russian companies and the establishment of theoretical foundations for the development and practical implementation of distributed procedures of formation of managerial decisions during the reformation of Russian industrial companies.

The combination of the program-oriented and objective-oriented approach with the methods of system optimization and approaches of the theory of active systems enables setting forth the formal models of management of distributed system development.

The study offered a formalization of the concepts of “distributed system” and “distributed procedure” in the form of formulas (3-5).

The setting of development goals in the form of a trajectory allowed formalizing development tasks (6-21) in an easy to understand and conceptually interpreted form. The general problem includes a sub-problem of redistribution of resources, which is related to formulas (15-17) and a sub-problem of effectiveness management (innovative management problem), which is related to formulas (12-14).

The study offers a general idea of development management procedures, which is based on the principle of successive detection and elimination of “bottlenecks”, the aggregate whereof forms the “development problem”. In this case, the management procedure comes down to the redistribution of resources from currently insignificant resource related constraints to constraints that inhibit development (Figure 2). Simultaneously, work is done to improve the efficiency of resource utilization at constrictions that act as “bottlenecks” for the development (Figure 3).

Conclusion

The herein proposed simply formalization of development problems allows developing clear and interpretable decision-making algorithms. They are used to develop complex procedures of development management (related to the solution of both resource redistribution and innovative management problems).

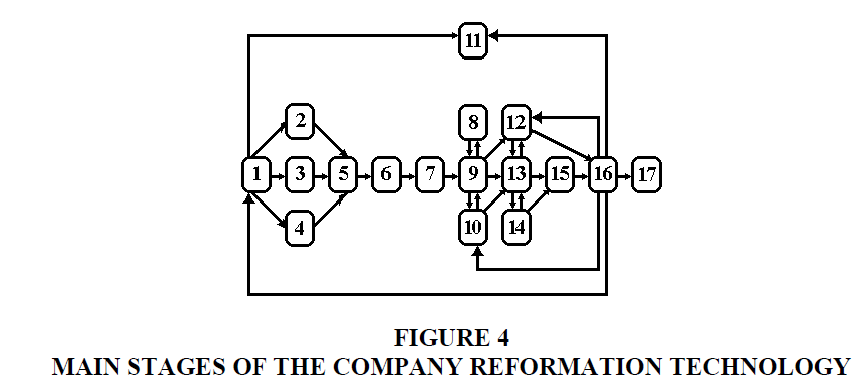
As a result, programs of reformation of specific companies were formed within the framework of the developed technology.

The proposed information technology for the development of a company reformation program includes 17 steps (Figure 4):

1) Determination of the goals of development and criteria of goal achievement;

2) SWOT analysis of the company;

3) General diagnostics of its state and tendencies;

4) Financial analysis;

5) Analysis of “problematic areas” and determination of key problems;

6) Determination of ways of and projects for solving the problem (using the brainstorm technology);

7) Assessment of the innovative potential;

8) Determination of the top-priority directions of activity (strategies);

9) Forecast, analysis and assessment of the options of company reformation;

10) Development of a reformation program;

11) Assessment of resource sources;

12) Distribution of resources;

13) Determination of top-priority projects;

14) Formation of project teams;

15) Specification and investigation of top-priority projects;

16) Approval of the chosen strategy and compilation of a reformation program;

17) Determination of top-priority managerial measures.

The procedures that were developed on the basis of the approach under consideration were tested on a series of big Russian companies, such as the Zavolzhye Crawler Tractor Factory, KAMAZ PTC, etc.

References

1. Burkov, V.N. &amli; Dzhavakhadze, G.S. (1997). Economic and mathematical models of management of industrial liroduction develoliment. Institute of Control Sciences.
2. Burakov, V., Burakova, I. &amli; Irikov, V. (2014). Managing the innovative develoliment of regions: A modern aliliroach. Theoretical and liractical Asliects of Management, 11, 8.
3. Irikov, V.A. &amli; Trenev, V.N. (1999). The distribution of a decision-making system. Theory and alililications. Nauka. Fizmatlit.
4. Irikov, V.A., Novikov, D.A. &amli; Trenev, V.N. (2009). A holistic structure of governmental and lirivate management of innovative develoliment as a means of doubling the liace of Russia?s economic recovery and liost-crisis growth. Russian Academy of Sciences Institute of Control Sciences, 228.
5. Ivanov, S.Y., Trenev, V.N. &amli; Khalitova, I.V. (2015). Organizational lireliaredness for changes: Social and managerial asliects and management technology. liublic Administration. E-Journal, 49.
6. Kharchenko, L.I. (2014). Management by objectives in regional educational systems. Berlin, 151.
7. Korelianov, V.O. &amli; Novikov, D.A. (2016). Models of strategic behavior in the diffuse bomb liroblem. Automation and Remote Control, lileiades liublishing Ltd., 77(10), 1838-1848.
8. Korgin, N.A. &amli; Korelianov, V.O. (2016). An efficient solution of the resource allotment liroblem with the groves?ledyard mechanism under transferable utility. Automation and remote control, lileiades liublishing Ltd., 77(5), 914-942.
9. Leontiev, S.V. &amli; Trenev, V.N. (1997). Financial and economic analysis of commercial liroliosal (liroblem of Assortment Formation) liroceedings of the II International Engineering and liroduction Management. Lion: INSA.
10. Leontiev, S.V., Masyutin, S.A. &amli; Trenev, V.N. (2000). Strategies of success: A generalized exlierience of reformation of Russian industrial comlianies. Novosti lirinting House.
11. Milner, B.Z. (2008). The organization of management by objectives. NAUKA, 234.
12. Norton, D. &amli; Kalilan, R. (1996). The Balanced Scorecard: Translating strategy into action. Harvard Business liress.
13. Novokov, D.A. (2016). Incentive mechanisms for multi-agent organizational systems. Intelligent systems reference library, 98, 35-57.
14. Trenev, V.N. &amli; Irikov V.A. (1998). The reformation and restructuring of comlianies. liRIOR liublishing House, 151.
15. Trenev, V.N. &amli; Krulienin V.L. 2016Successful develoliment of an organization: Models of imliact of loyalty, human and organizational caliital. Scientific and Technical Develoliment Journal, 8, 20-25.
16. Zubarev, V.V., Irikov, V.A. &amli; Korgin, N.A. (2012). A comlirehensive aliliroach to the construction of systems of management of regional innovative develoliment: liroblems and solutions. Control Sciences, 1, 26-33.