Keywords

Fama-Macbeth Procedure (1973), The Fama and French Three-Factor Model (1993), The Fama and French Five-Factor Model (2015), The Egyptian Stock Market, The Cross-Sectional Regression, Emerging Markets, Inflation Rate And Exchange Rate.

Introduction

The high importance and significance of Assets Pricing Models pushes the researchers to identify, evaluate, and test the determinants of stock returns to capture complete cross-sectional variation of stock returns. The Portfolio managers, Financial Advisors and individual investors can trust and rely on these models to measure risk, then select financial assets and construct their diversified portfolios to eliminate the unsystematic risks and maximize their returns. Moreover, the investors can decide if the market can reward them for the accepted level of risk. On other hand, the firms use the Assets Pricing Models in capital budgeting decisions to select among different investment alternatives in order to execute projects with the appropriate hurdle rate (Gregory et al., 2013).

Dash & Mahakud, (2014) argued that the developed markets have radically nature and characteristics differ from the emerging markets. Moreover, Drew & Veeraraghavan (2002), state that the emerging markets can provide an out-of-sample test due to the different economic, political, structural, and institutional factors compared to the developed market. Accordingly, to generalize the results of these studies and to confirm the validity and applicability of these models in different contexts, the researchers conduct and test the assets pricing models in emerging market. Elsayed (2018), The Egyptian market is one of the emerging markets, which has low trading volume, small number of listed firms in stock exchange market, illiquidity, weak corporate governance, and a little number of investment research institutions.

However, there is a limited number of studies examine the effect of inflation and foreign currency fluctuation on performance of the Fama and French models. The core of the research to fill the research gap while the application will take place in the Egyptian stock market. As a result of the above and based on future research/recommendation we start to build our contribution area by considering some of macroeconomic variables to The Fama and French models (Jiao & Lilti, 2017) to control the effect of inflation rate and foreign currency fluctuation. the main concern of financial markets player and foreign investors is evaluating their investment in real returns expressed in US dollar to enable them evaluating between the different emerging stock markets and exploiting the opportunities of them.

Literature Review

Capital Assets Pricing Model (CAPM)

Assets pricing model was developed by Treynor (1962) and Sharpe (1964), while this model extended and defined by Lintner (1965) and Mossin (1966) (Sharpe – Lintner Capital Asset Pricing Model). the only factor affecting the returns of stocks is systematic risk, which cannot eliminate by the well diversified poertoflio. Accordingly, the compensation for bearing this systematic risk is the excess return of the risk-free rate, which is called market risk premium as below equation:

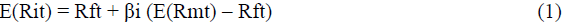
Where, E(Rit) = The expected return on asset I, Rft = the risk-free rate, E(Rmt) = the expected return of the market portfolio, E(Rmt)-Rft = Risk Premium & βi = market beta of asset

i.
However, the main criticisms of CAPM are unrealistic assumption (no taxes, no transaction costs, efficient market, perfect competition, investors are price taker, investors can lend, and borrow at the risk-free rate. the investors are rational, have homogenous expectations and Finally, the model is single period investment horizons). Moreover, the failure of market beta only to explain the stock returns variation, which lead to emerge of the multifactor models.

Multifactor Models

Arbitrage Pricing Theory (APT)

Rose (1976) developed the Arbitrage Pricing Theory. The APT assumes multiple factors explain assets returns as an alternative model to the CAPM. The Arbitrage Pricing Theory links macroeconomic factors and stock returns by predicting the rate of return in linear function of various factors as below equation:

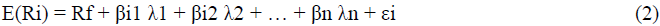
Where, E(Ri): the expected return on asset I, E(Rf): the risk-free rate, βik: assets beta sensitivity to the kth factors, λ_k: the risk premium of the factor, k: (1,2,….n) number of the factor & εi: residuals of regression model

Fama and French Three-factor Model (FF3)

Fama & French (1992), suggest firm size and book-to-market ratio risk factors can explain the variation of stock returns, which can’t capture by market beta only. Fama & French (1993) propose the three-factor model by applying the time series regressing approach of Jensen et al. (1972), this model extends the CAPM by adding two risk factors: Size (SMB) and Value (HML). The size factor measures the excess average return of the small stock portfolio, while the value factor measures the excess average return of the high B/M ratio portfolio as below equation:

Rit – Rft = αi + βi1 (Rmt – Rft) + βi2 (SMBt) + βi3 (HMLt) + εi (3)

Where, αi = intercept of the regression line, Rit=total return of a assets i at time t, Rft = risk-free rate of return at time t, Rmt = returns of market portfolio at time t, Rit−Rft= expected excess return, Rmt−Rft = excess return on the market portfolio, SMB; is the size premium (Small Minus Big), HML; is the value premium (High Minus Low) and εi: Residuals of regression model & βi1,2,3= Beta values of the three independent variables; Rmt-Rft, SMB, HML

Fama and French Five-Factor Model (FF5)

Fama & French (2015) consider additional two factors: profitability and investment by applying the valuation theory. The examining of those two factors results that proved positive relationship between profitability and expected stock returns and negative relationship between investment rates and expected stock returns not proved yet. The main limitation of this model is the failure of explaining variation of small stocks of the firms that invest aggressively and have low profitability. Fama and French Five-factor model (FF5) is expressed as below equation:

Rit – Rft = αi + βi1 (RMt – Rft) + βi2 (SMBt) + βi3 (HMLt) + βi4 (RMW) + βi5 (CMA)+ εi (4)

Where, RMW; is the profitability premium (Robust Minus Weakness) and CMA; is the investment premium (Robust Minus Weakness). The other terms are as in (3) above

Research Methodology

This section presents the main methodology employed to run the test on the Fame and French Models. the asset pricing models can be tested by using the econometrics techniques either the traditional beta frameworks, which includes time series regression and cross-sectional regression approaches, or the main approach of stochastics discount framework is Generalized Method of Moments (GMM) approach. These approaches argued by Lozano (2009). This study applies one of the traditional beta frameworks is the cross-sectional regression approach as the main test methodology on The Fama and French models (1993, 2015). The cross-sectional regression is the simplest way to capture the variation of average excess returns of stocks or portfolios on estimated betas (βik) and then estimate the factor risk premia (??) by applying the Ordinary Least Square (OLS) regression (Cochrane, 2001) as below equation:

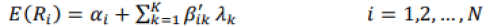  (5)

Where, N: is the number of assets, k: is the number of risk factors, (λk): the estimated risk premia & ??: the pricing errors. To test estimated risk and pricing error using Fama-Macbeth procedure (1973). The Fama MacBeth Cross-Sectional Regression is one of the common approaches is testing asset pricing models. The Fama-MacBeth cross-sectional regression has a two-pass regression framework; firstly, estimate betas by running a time-series regression. specifically, the rolling time-series regression to obtain estimates of time-varying betas. for each stock there are T − 24-time series regressions as below equation (under assumption of rolling regression of 24 months, Abdou, 2019):

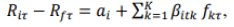
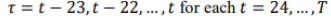     (6)

Secondly, estimate the factors’ risk premia and the intercept by applying a monthly cross-sectional regression as below equation:

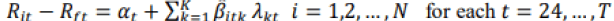      (7)

Data Collection

The data for this study is historical data. This data set includes monthly real returns, size, book equity, book-to-market ratio, operating profit, operating profitability ratio, total assets and investment ratio for a sample of (136) stocks of non-financial firms only listed in the Main Egyptian stock market. The sample period is starting from July 2005 to September 2019 after excluding February and March of 2011 (The EGX Market is officially closed due to January Revolution). The accounting data employed in this study are extracted from audited and Published financial statements, which collected from EGX Information Center, Egypt for Information Dissemination (EGID) company and the missing has been already downloaded from Mubasher website. The data of macroeconomic factors are downloaded and collected from Central bank of Egypt (CBE) website and Central Agency for Public Mobilization and Statistics (CAMPAS) website. Finally, the market data are downloaded from Thomson’s Reuters (EIKON). The basic variables used in this paper and their description are shown in Table 1.

Table 1 Variables Description
Variables	Symbols	Description
Dependent Variable
Monthly Return	Rit	(Pit-Pit1)/pit1
Individual Stock Risk Premium	Rit-Rft	Excess return of stock (i) at time (t)
Independent Variables
Market Return	RM	Monthly Value-weighted average of return of all selected stocks in portfolio.
Risk Free Rate	Rft	Three (3) months treasury bill rate.
Market Risk Premium	RM-RF	Excess return of market return (Rm) and risk free rate (Rf)
Size	SMB	Market capitalization (ME); No. of our standing shares * Adjusted closing price of each month
Value	HML	Book-to-Market Ratio; BE/ME
Operating Profit	OP	Earnings Before Taxes; EBIT minus Interest Expenses
Profitability	RMW	Operating Profit divided by Book Equity (OP/BE)
Investment	CMA	The growth in total assets; the Change of total assets (t-2 & t-1)/total assets t-1
Exchange Rate	ER	Monthly rate expressed in US Dollar
Inflation Rate	Inf.	Monthly Consumer price index (CPI).

Portfolio Construction Of The Fama And French Factors

The aim of this section is to summarize the construction of the Fama and French factors given. According to Fama & French (1993, 2015), the portfolios are constructed on June of each year t using accounting data from December of year t-1, while the returns for July of year t to June t+1. The main objective of six (6) months gap between the end of fiscal year on December and the date of constructing the portfolio to ensure that all necessary accounting data are available and known after closing, auditing and disclosure the financial statements at the time of constructing portfolio.

The portfolios construction of risk factors; SMB, HML, RMW & CMA factors are formed based on 2x2 sorts on the size, the B/M ratio, the operating profitability ratio & Investment ratio (Ragab, 2019). Fama & French (2015) stated that the three sorting approaches have the same description of the average returns and there is no superior approach is preferred over the others. Moreover, Fama and French justify applying the (2x3) sorting approach by an arbitrarily selection. Finally, due to the nature of Egyptian stock market which has an unavailability of data and lower number of listed firms the 2x2 is better for diversification of all stocks in the sample. Abd (2016) recommends using the 2x2 sorting approach. While Ragab (2019), applies the 2x2 portfolio construction sorts. Accordingly, this study considering the recommendation regarding the sorting approach of portfolios.

The Fama-French five-factor model has five portfolios: RM-RF, SMB, HML, RMW and SMB and HML factors are calculated as follows. First: at the end June of year t, stocks are sorted ascendingly based on their market capitalization, which calculated as adjusted stock prices times the number of outstanding shares. Firms that have negative B/M ratios are excluded when determining the B/M ratio breakpoint. Then calculate the breakpoint of the size portfolio, by     using 90th percentile of the total market capitalization as Big stocks (B) while the 10th percentile of total market capitalization as Small Stocks (S), (Cakici et al., 2013), Accordingly the stocks are classified into two size groups: Big and Small. then stocks are arranged in an ascending order according to their Book-to-Market ratio.

The justification of using this breakpoint for size factor is the nature of Egyptian Stock market, which has limited no. of listed firms, the unavailability of the data and a relatively small market capitalization. The median of NYSE size breakpoint for developed markets Fame & French (2012) is too large compared to the Egyptian stock market as emerging market which results misallocation and un representable size portfolios by listing a limited number of firms in the big portfolio. To avoid this point of weakness - with respect to the nature of Egyptian stock market - applying the approach of Cakici et al. (2013), who suggests applying the market share-based approach to determine the breakpoint of size factor at emerging markets instead of NYSE median based approach at developed markets. The market share-based approach ensures that both size portfolios (Small and Big) include the equivalent shares of the total market capitalization as NASDAQ, AMEX and NYSE stocks.

Stocks whose Book-Market ratio are less than median are defined as Growth Stocks and labeled Low (L), while stocks whose Book-Market ratio are more than median are defined as Value Stocks and labeled High (H), as a result of the intersection of the two size groups and the two Book to market groups, four portfolios are constructed as follow SL, SH, BL, and BH. For each one of these portfolios, the monthly value-weighted returns are calculated from July of year t to June of year t+1. To construct the SMB factor, calculate the average of the two Small stocks portfolios minus the average of two Big stocks portfolios as below equation:

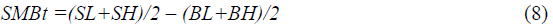
Similarly, to construct the HML factor, calculate the average return of the two High Book-To-Market ratio stock portfolios minus of the average returns of the two Low Book-To-Market ratio stock portfolios as below equation:

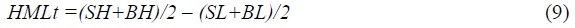
The profitability (OP) and investment (Inv.) factors are calculated similar to Fama and French (2015), operating profitability is calculated as Operating income (EBIT) divided by Book Equity (BE). Both variables are from the end of fiscal year t-1 and used to construct portfolios in June of year t. To calculate the profitability factor (RMW), stocks are arranged to two groups based on their OP ratio. Stocks whose OP ratio is less than median are defined as Weak (W), while stocks whose OP ratio is more than median defined as Robust (R). As a result of the intersection between the two size groups and the two operating profitability groups, four portfolios are constructed: SW, SR, BW, and BR.

For each one of these portfolios, the monthly value-weighted returns are calculated from July of year t to June of year t+1. To construct the ????? factor, calculating the average returns of the two small stocks portfolios minus the average returns of two Big stocks portfolios as below equation:

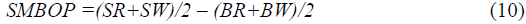
To construct the RMW factor, calculating the average returns of the two High OP/BE stock portfolios minus the average returns the two Low OP/BE stock portfolios as below equation:

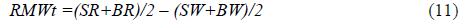
Finally, the total asset growth has been employed as a measure of investment factor. The Investment ratio used to construct portfolios in June of year t is calculated as the percentage change in total assets from the end of fiscal year t-2 to the end of fiscal year t-1. To calculate the investment factor (CMA), stocks are ordered and classified to two groups based on their asset growth: stock whose asset growth is less than median are defined as Conservative (C), while stocks whose asset growth is more than median are defined as Aggressive (A), According to the intersection of the two size groups and the asset growth groups, four portfolios are constructed: SC, SA, BC, and BA. For each one of these portfolios, the monthly value-weighted returns are calculated from July of year t to June of year t+1. To construct the factor, calculating the average returns of the two small stocks portfolios minus the average returns of the two Big stocks portfolios as below equation:

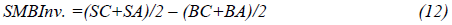
To construct the CMA factor, calculating the average returns of the two Conservative asset growth stock portfolios minus the average returns of the two Aggressive asset growth stock portfolios as below equation:

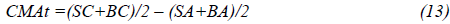
The construction of CMA and RWM factors creating the two additional size factors which are SMBOP and SMBINV. The SMB of the Fama and French five-factors model is calculated as the average of SMBBM, SMBOP and SMBINV as below equation:

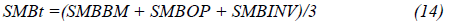
Data Analysis

Descriptive Statistics

The aim of this section to summarize the results of descriptive statistics of The Fama and French Factors as below table (2). The monthly average of excess returns of market (RM-RF) or equity premium for The Fama and French Five-factor model are -1.028% (t=-1.775782, P-Value = 0.0775), which equivalent to -12.336 per year, however the market factor is statistically significant at significance level (10%). While the monthly standard deviation of market factor is high 7.53% and refers to fluctuation of The Egyptian stock market witnessed during the sampling period, which lead to high annual real returns.

Table 2 Descriptive Statistics For The Ff Factors
Factors	Mean (%)	Standard Deviation (%)	Sig. Level (Mean = 0) (%)	Min.	Max.	Skewness	Excess Kurtosis	Jarque-Bera (Sig. Level)
MKT	-1.028	7.53	7.75	-0.49993	0.28827	-1.10233	11.20361	918.1036
SMB(BM)	0.846	6.21	7.79	-0.15842	0.20461	0.58394	1.272253	21.00247
SMB	1.54	8.46	1.92	-0.17179	0.41450	1.06415	3.742798	130.5399
HML	0.132	6.30	78.56	-0.28280	0.24882	-0.90470	5.633702	246.5467
RMW	-0.204	5.47	62.94	-0.28342	0.30083	0.12916	8.901062	558.3735
CMA	0.121	4.35	71.95	-0.21332	0.16471	-0.34216	4.192752	127.0843

Similar to the market factor; consistent to Fame and French 2015 and the previous studies in Egypt; the monthly average SMBBM returns (Size Premium) are near zero 0.846% (t=1.773, P-value = 0.0779), which is equivalent to 10.15% per year, however the size factor is statistically significant at significance level (10%). While the monthly standard deviation of size factor is high 6.21%. The monthly weighted average SMB (SMBBM, SMBOP, SMBINV) returns (Size Premium) are 1.54% (t=2.364211, P-value = 0.01921), which is equivalent to 18.48% per year, however the size factor is statistically significant at significance level (5%). While the monthly standard deviation of size factor is 8.46%. These results support Fama & French (1993) and reflect the existence of size effect in Egyptian stock market and show that the small stocks which has small market capitalization outperform the big stocks, which have big market capitalization during the sample period.

The monthly average HML returns (Value Premium) are 0.132% (t=0.272365, P-value = 0.7856). which is equivalent to 1.584% per year, however the value factor is statistically insignificant. While the standard deviation of value factor is high 6.30%. These results support Fama & French (1993) and Avramov & Chordia (2006) and Inconsistent with (Ragab, 2019). These results reflect the absence of value effect in Egyptian stock market and show that the value stocks which have high B/M ratio outperform the growth stock, which have low B/M ratio during the sample period.

The monthly average RMW returns (Profitability Premium) are near zero -0.204% (t=-0.483493, P-value = 0.6293), which equivalent to -2.49% per year, however the profitability is statistically insignificant. While the standard deviation of profitability premium is high 5.47%. These results support Abd (2016) and Ragab (2019). Moreover, these results reflect the absence of profitability effect in Egyptian stock market. Finally, the monthly average CMA returns (Investment premium) are 0.121% (t=0.359780, P-value = 0.7194), which equivalent to 1.45% per year, however the investment premium is statistically insignificant. While the standard deviation of investment premium is high 4.35%. Consistent to (Abd, 2016) who proves that the investment risk factor has no effect in Egyptian stock market. However, these results contradict with Ragab (2019). These results reflect the absence of investment effect in Egyptian stock market.

Table 3 Shows the correlation matrix between the risk factors. equity premium and size premium are high negatively correlated (-0.3341). equity premium and value premium are positively correlated (0.14623). equity premium and profitability premium are positively correlated (0.1508). equity premium and investment premium are positively correlated (0.21252). size premium and value premium are negatively correlated (-0.0895). size premium and profitability premium are weakly positive correlated (0.01170). size premium and investment premium are negatively correlated (-0.0819). Value premium and profitability premium is negatively correlated (-0.2582). value premium and investment premium are negatively correlated (-0.2198). profitability premium and investment premium are positively correlated (0.1232). The largest correlation value is (-0.3341) between equity premium and size premium. The lowest correlation value is (0.01170) between size premium and profitability premium.

Table 3 Correlation Matrix For 5 Ff Factors
Factors	MKT	SMB	HML	RMW	CMA
MKT	1.00
SMB	-0.334106	1.00
HML	0.146235	-0.0895155	1.00
RMW	0.150832	0.0117046	-0.258264	1.00
CMA	0.212529	-0.0819278	-0.219871	0.123207	1.00

Inconsistent with Fama & French (2015); Size factor has a negative correlation with the market factor, in addition to the value, investment and profitability factors are positively correlated with market factor. Also the size factor is positively weekly correlated with profitability factor. However, Consistent with Fama and French; the size factor is negatively correlated with investment factor. Furthermore, the value factor is negatively correlated with the profitability and investment factors in contradiction with Fame & French (2015), which stated that the value, profitability and investment risk factors are positively correlated, while these results support the results of (Ragab, 2019). Accordingly, the correlation values show that each risk factor is independent from the other. Finally, there is no Multicollinearity problem exists among the risk factors.

To sum up, descriptive statistics of The Fama and French factors highlight reflect the absence of the value, profitability, and investment risk factors over the selected sampling period.

Fama andFrench Performance Summary

Table 4 show that the intercept is positive, economically, and statistically significant (P-value = 0.00132, P-value = 0.00069) for Fama and French Three and Five Factor respectively, which explain that the models fails to capture the cross-sectional variations in stock returns. However, the intercept of the risk premia of Fama and Fench Three factor model provides more supportive evidence than the five-factor model.

Table 4 Fama-Macbeth Cross Sectional Regression Test On Individual Stocks Using Rolling Betas
Individual Stocks	a	?M	?SMB (3FF)	?SMB(5FF)	?HML	?CMA	?RMW
Coefficient	0.01391 (FF3) -0.01615 (FF5)	0.007614393	0.001784	-0.001824	-0.0042932	-0.000718	0.001889
t-statistics	(3.3930)***	(4.76530)***	1.01067	-1.01585	(2.92735)***	-0.98080	(1.6820)*
FF Factors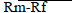
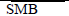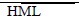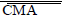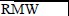Sample Average Return		-1.028%	0.846%	1.538%	0.1319%	0.1205%	-0.2034%

Note: Table 4 present the intercept and slopes of the Fama-MacBeth cross-sectional regression of monthly real excess return for individual stocks based on their rolling regression betas. T-statistics reported om brackets are derived from heteroscedasticity and autocorrelation consistent regression for. The t-statistics based on Shanken’s (1992) correlation are given in square brackets. The results are obtained from the following regression:  

The market risk premium (MKT) is positive and economically and statistically significant at significance level (1%) (P-value = 0.0000, P-value = 0.0000) for Fama and French Three and Five Factor respectively, which explain that the MKT factor is significantly priced in the Egyptian stock market. These results are contradicting with (Lewellen et al., 2010). The size risk premium (SMBBM) for Fama and French three factors is positive and statistically insignificant (P-value = 0.3121), while the size risk premium (SMBBM, OP, Inv.) for Fama and French five factors is negative and statistically insignificant (P-value = 0.3097).

The value risk premium (HML) is negative and significant at significance level (1%) (P-value = 0.0069, P-value = 0.0034) for Fama and French Three and Five factors respectively, which explain that the HML factor is significantly priced in the Egyptian stock market for the Fama and French Three and Five factor models. The investment risk premium (CMA) factor is negative and not statistically priced (P-value = 0.3266) in the Egyptian stock market. Finally, the profitability risk premium (RMW) is positive and significant and significance level (10%) (P-value = 0.0925) which explain that the RMW factor is significantly priced in the Egyptian stock market.

Accordingly, the results of the rolling regression technique show that the Fama and French Three and Five factor models fail to capture the cross-sectional variation of stock returns and cannot be accepted as a valid asset pricing model for the Egyptian stock market. These models produce high significant intercept or pricing error for three and five factor model (P-value = 0.0013, P-value = 0.00069) respectively. Moreover, to enhance the results can apply more advanced approaches to capture the time variation in betas rather than rolling regression model like; scaled factor models or predictability test. The Fama and French Three Factor model outperforms the Fama and French Five Factor model in Egyptian Stock market. Finally, the Egyptian stock market rewards the inventors for market, value, and profitability risk factors.

* reflects significance at 10% level
** reflects significance at 5% level
*** reflects significance at 1% level

Conclusion

The emerging markets consider proposing market due to the opportunities of the growth. Although, the emerging markets have a special nature and face difficulty to capture the cross-sectional variation of stock returns by using the standard assets pricing models (Dash & Mahakud, 2014, Drew & Veeraraghavan, 2002). Egypt is one of the emerging markets (El sayed, 2018) attracts the Foreign Direct Investment (FDI) and investors. Accordingly, there is a severe and urgency requirement to find a valid asset pricing model to be used by financial market players. The importance of this model is to evaluate risk and return of their investment, make rational investment decision, allocating their fund to different alternatives investment pools and exploit the investment opportunity of the emerging markets (Gregory et al., 2013, Abdou, 2019, Rabab, 2019).

Under assumption of the real return expressed in US dollar, the results of descriptive statistics show that the size and market risk factors are statistically significant anomalies in the Egyptian stock market and existed. Furthermore, consistent with Fama & French (2015) and previous studies, while the value, profitability and investment risk factors are absent in The Egyptian stock market. Although the results provide some evidence for the existence of these factors. The Fama and French Models fail to capture the cross-sectional variation of stock returns and produce large number of significant alphas. Finally, the Egyptian market reward the investors for the market, value and profitability risk factors only. The results of this thesis support the previous studies in Egypt and consistent with (Abd, 2016; Abdou, 2019; Ragab; 2019). The considering defined macroeconomic variables in this study; inflation rate and foreign exchange rate lead to weaken the explanatory power of different Fama and French models in Egypt.

Future Research

This study recommends testing new variables at the micro and macro level (Salameh, 2015; Abdou, 2019) and Developing a new technique for constructing the portfolio to overcome the limited number of sample (Salameh, 2015; Regab 2019). Furthermore, the results suggest testing the presence of the value effect using other variable such as: (E/P), (CF/P), (D/P) and sales growth (Abd, 2016). Otherwise, use Retrained Earnings/Market Equity ratio as proxy for value risk factor (Ray et al., 2019). The profitability risk factor can be measured by Gross profitability (Novy Marx, 2013) instead of the operating profitability (OP). Ghysels (1995), Researchers shall determine the best fit model specification by relaxing the assumptions of constant betas and risk premia to provide better explanations of stock returns (Abdou, 2019). Finally, Test new aspect of the behavioral finance, which can result low significant alphas.

References

Abd, R. (2016). Determinants of stock returns: Evidence from Egypt. Master Thesis, the American university in Cairo.

Banz, R. (1981). The relationship between return and market value of common stocks. Journal of Financial Economics, 9, 13-18.

Black, F., Jensen, M., & Scholes, M. (1972). The Capital Asset Pricing Model: Some Empirical Tests. Studies in the Theory of Capital Markets New York: Praeger Publishers.

Cochrane, J. (2001). Asset Pricing. 1st edition, Princeton University Press.

Dash, S., & Mahakud, J. (2014). Do Asset Pricing Models Explain Size, Value, Momentum and Liquidity Effects? The Case of an Emerging Stock Market. Journal of Emerging Market Finance, 13(3), 217-251.

Drew, M. et al. (2003). Firm size, book-to-market equity and security returns: Evidence from the Shanghai Stock Exchange. Australian Journal of Management, 28(2), 119-139.

Drew, M., & Veeraraghavan, M. (2001). Explaining the cross-section of stock returns in the Asian region. International Quarterly Journal of Finance, 205-222.

Drew, M., & Veeraraghavan, M. (2002). A Closer Look at the Size, Value Premium in Emerging Markets: Evidence from the Kuala Lumpur Stock Exchange. Asian Economic Journal, 16(4), 337-351.

El Sayed, S. (2018). Testing Factor Models in Emerging Markets: Evidence from the Egyptian Stock Market. Working paper.

Fama E.F., & French, K.R. (2015). five-factor asset pricing model. Journal of Financial Economics, 116, 1-22.

Fama, E., & Macbeth, J.D. (1973). Risk, Return and Equilibrium: Empirical Test. The Journal of Political Economy, 81, 607-636.

Fama, E.F., & French, K.R. (1993). Common Risk Factors in the Returns on stocks and bonds. Journal of Financial Economics, 33(1), 3-56.

Ghysels, E. (1995). On Stable Factor Structures in the Pricing of Risk. Working Paper No. 95s-16, CIRANO Scientific Series.

Gregory, A., Tharyan, R., & Cistidis,A. (2013). Constructing and Testing Alternative Version of the Fama-French and Carhart Models in the UK. Journal of Business Finance and Accounting, 40(1), 172-214.

Jiao, & Lilti. (2017). Whether profitability and investment factors have additional explanatory power comparing with Fama-French Three-Factor Model: empirical evidence on Chinese A-share stock market. China Finance and Economic Review, 5(7).

Khaled, L. (2017). The Relationship Between Interest Rate and Stock Market Index: Empirical Evidence from Arabian Countries. Research Journal of Finance and Accounting.

Lozano, M. (2009). Econometrics of Asset Pricing: Methodological Review and Empirical Exercise.

Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91.

Mohamed A.S., & Khairy, E. (2014). Comparison of Asset Pricing Models in the Egyptian Stock Market. Accounting and Finance Research, 3(4).

Mossin, J. (1966), Equilibrium in a Capital Asset Market. Econometrica, 34(4), 768-783.

Muhammad I.A., Ramiz, R., Awais, R. (2010). Do Interest Rate, Exchange Rate Effect Stock Returns? A Pakistani Perspective. International Research Journal of Finance and Economics ISSN 1450-2887 Issue 50 (2010) Euro Journals Publishing, Inc. 2010.

Nabila, N. (2015). Impact of Macroeconomic Variables on Stock Returns: Evidence from Bombay Stock Exchange (BSE). Journal of Investment and Management, 4(5), 162-170.

Nada S.R. (2019). A Comparative Study between the Fama and French Three-Factor Model and the Fama and French Five-Factor Model: Evidence from the Egyptian Stock Market. International Journal of Economics and Finance, 1.

Novy Marx, R. (2013). The Other Side of Value: The Gross Profitability Premium. Journal of Financial Economics, 108(1), 1-28.

Rabab, A. (2019). Determinants of Stock Prices in The Egyptian Stock Market: Traditional Asset Pricing Models versus Behavioral Asset Pricing Models. PhD thesis, Faculty of Business and Law, University of the West of England, UK.

Rehab T., & Khairy, E. (2016). A Five-Factor Asset Pricing Model: Empirical Evidence from Egypt. International Journal of Business, 21(4).

Salameh, H.M., et al. (2015). Implement Fama and French and Capital Asset Pricing Models in Saudi Arabia Stock Market. The Journal of Applied Business Research, 31(3).

Seri, S. et al. (2015). Impact of Exchange Rate on Stock Market. International Journal of Economics and Financial, Issues ISSN: 2146-4138.

Sharpe, W.F. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Uncertainty. Journal of Finance, 19, 425-442.