Keywords

PGARCH, Leverage Effect, Gold Price, Conditional Volatility, ADF Test.

Introduction

Since ancient times, gold was accepted as a universal means of the exchange (Tripathi, Parashar, & Singh, 2014). It is considered as a safe investment and used in large quantities during festivals and ceremonies in India. Gold has been a sizeable component of the portfolios of Indian households. The gold price seems to have an upward trend throughout, even during the recession and people use gold as a status symbol (Bhunia & Das, 2012). The price changes in gold affect almost every investor in India. Hence analysing the volatility of gold gained importance in the recent years (Tully & Lucey, 2007).

The volatility of an asset is quantified through the estimation of conditional variance (Engle, 1982). Estimating and forecasting volatility is an essential task in portfolio management, equity and derivative instrument pricing and risk management (Kalu, 2010). Empirical evidence documents various features of the volatility in asset returns. The volatility estimates in the past had found features like, volatility clustering, fat tail distribution and asymmetry or leverage effects (Miron & Tudor, 2010). Volatility clustering is observed, when large asset price changes are followed by large changes in asset prices and small asset price changes are followed by small asset price changes of either sign. Asymmetry is a situation where a negative innovation leads to an increased next period volatility than a positive innovation (Engle & Patton, 2001). The asymmetric effect is otherwise known as leverage effect because volatility responds to positive and negative innovations differently.

The remainder of the paper consists of an overview of conditional heteroskedasticity models followed by a review of literature and research methodology. The discussion on the results and conclusion are presented at the end of the paper.

Overview Of Conditional Heteroskedasticity Models

Auto Regressive Conditional Heteroskedasticity (ARCH) model was developed by Engle (1982) and extended by Bollerslev (1986) and Nelson (1991). ARCH model was an important improvement over the rolling standard deviation, which was used as a measure of volatility in those days (Engle, 2001).

GARCH (Generalized Autoregressive Conditional Heteroskedasticity) Model

Bollerslev (1986) generalized ARCH model developed by Engle (1982). He defined conditional variance as an Autoregressive Moving Average (ARMA) process. GARCH process introduces the lagged conditional variance as a regressor (Bollerslev, 1986).This generalization enabled the model to produce better results with few lags. The general specification of GARCH (1,1) model is given in equation (1).

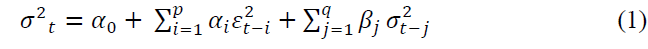
Where 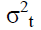is the variance for the time period t. α_i and β_j are coefficients. ε_t-i is the lagged residual from the mean equation and 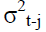is the lagged variance from the period t_-j. Variance is always a positive number. In order to satisfy this constraint, α_i>0 and β_j>0 was also specified. The GARCH (1,1) model has three components, the constant 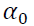, the news about volatility from the previous period (ARCH term 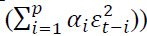and the last period’s forecasted variance (GARCH term 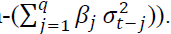An ordinary ARCH model is a special case of a GARCH specification where no lagged variances are included in the equation (Tripathi & Seth, 2016).

Threshold GARCH (TGARCH) Model

TGARCH model estimates the variance as a function of a constant, lagged residual term and lagged forecast variance. Symmetrical models like GARCH and ARCH assume that the lagged positive and negative residuals (innovations) have the same impact on the variance. But it was observed in the past that bad news has larger impact on volatility compared to a good news (Ding, Granger, & Engle, 1993). Asymmetrical models estimate an asymmetric or leverage coefficient (γ_i), which can test the presence of an asymmetric effect. The general form of TGARCH model is given in equation (2) (Glosten, Jagannathan, & Runkle, 1993).

Where 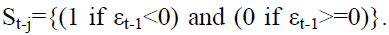In TGARCH model (2) positive shocks 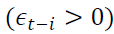and negative shocks 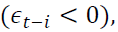have differential effects on the variance. The impact of good news is measured by the coefficient 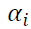and the impact of bad news is given by the sum of coefficients 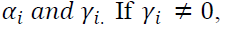then it indicates the presence of leverage effect which means negative shocks to the price of an asset leads to a higher next period volatility.

Power GARCH (PGARCH) Model

Conditional varinace is assumed as a linear function of lagged squarred residuals in GARCH model (Ding, Granger, & Engle, 1993). But in the literature, high autocorrelation was found for power transformed absolute returns than the actual returns (Nelson,1991). Hence, models based on power transformed residuals must perform better than GARCH models.

Ding, Granger and Engle (1993) suggested a new class of model called Power ARCH. This model allowed the coefficients to be either positive or negative and estimates the power transformation term (δ) in the equation. Traditionally data transformation involved the use of the squared term. However when the data is not normally distributed or when it is not otherwise possible to characterize the distribution by the mean and variance, the use of a squared power transformation is not appropriate (Ding, Granger, & Engle, 1993). Other power transformations are required to use higher moments to describe the distribution adequately. The general form of PGARCH model is presented in equation (3).

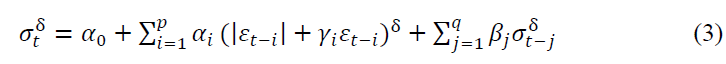
Where 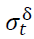is the variance for the time period t, 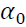is the unconditional variance or the constant, 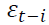is the lagged residuals from the mean equation and 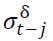is the lagged forecasted variance. When 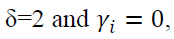P-GARCH would become GARCH model (Tully & Lucey, 2007).

Review Of Literature

Christie, Chaudhry & Koch (2000) analyzed the impact of macro-economic announcements on the intraday data of gold and silver prices in the US for the period 1992-1995. Linear Regression was used to analyse the impact of the news announcements. The asset price variance was found to be very high in the news announcement days than the non-announcement days. Gold and silver prices were actively responding to the CPI, unemployment rate and GDP announcements. Worthington & Pahlavani (2006) emphasized the stable relationship between gold price and inflation rate and they insisted that gold be an appropriate hedge against inflation in the US. Tully & Lucey (2007) found that APGARCH model was a good fit for examining the conditional volatility of gold prices in the UK. They used likelihood ratios to test the goodness of fit. They also analysed the impact of macroeconomic variables on the conditional volatility of gold price in the UK. Among the macroeconomic variables studied, only US dollar was found to have a significant impact on the gold price.

Singh & Singh (2010) examined the linkages of stock markets of India and China with the United states stock market. Using Granger causality, they found Unidirectional causality from US markets to Indian stock market and suggested that short term diversifications are limited beteween Indian stock market and the US stock market.

Toraman, Ba?ar?r & Bayramo?lu (2011) modeled the conditional variance of US gold price using M-GARCH model for the period of 1992-2010. They found evidence for an inverse relationship between US exchange rate and US gold price and significant positive relationship between gold and oil prices. They also suggested that gold may be used as a hedge against US dollar. Mishra (2014) felt that gold is one of the best investment choices and the best alternative for US dollar. Gencer & Musoglu (2014) applied GARCH model to the gold price in Turkey and found that past volatility of stock market returns influences the current volatility of gold price. Singh & Kaur (2015) anaysed the stock market linkages and volatility spill overs using Tri-variate Vector autoregression and TGARCH (1,1) during period of 2007 to 2009. They found unidirectional causality from US market to Indian market. They also found a unidirectional volatility spillover from the US market to Indian market.

Statement Of The Problem

The amount of literature in the field of volatility modeling of gold price is limited. Most of the literature on gold price were on the causal relationship of gold price either on the stock market returns or on the macroeconomic variables. There are very few studies in the past which focused on the estimation of conditional volatility of gold price. As gold occupies an imporatnt place in almost every Indian’s portfolio, it is imperative to estimate the conditional variance of the gold price in India. There were no studies in the literature which estimated the conditional volatility of gold price in India. This study attempts to model the conditional volatility of gold price in six major cities in India using PGARCH moel. Gold price in India varies significantly between cities. This is due to the factors like, transportation cost, state taxes. Hence, the gold price observed on a particular day is usually be different between cities in India. Major cities where gold is consumed in huge quantity were chosen for this study. The cities chosen for the study were Bengaluru, Chennai, Delhi, Hyderabad, Kolkata and Mubai.

Studies in the literature also suggests that US stock market return influences the stock return and volatility of Indian stock market. An attempt was made in this study to test, whether the same phenomenon is found in gold market in India as well. Hence this study analyzes the impact of US gold price on the volatility of gold prices in the selected Indian cities.

Objectives Of The Study

1. Examine the presence of volatility clustering and asymmetric effect feature in gold price volatility in India.

2. Investigate the impact of US gold price return on gold price volatility in India.

Research Methodology

This study is entirely based on secondary data. The daily US gold price data were acquired from the database of World Gold Council and the daily gold price in Indian cities were collected from website www.goldratecity.com. The price of gold in the United States was collected in US Dollar per troy ounce. This rate was then converted into price per gram and was expressed in US Dollar. The sample period for the study was from 1, January 2011 to 31, August 2017 (1,686 daily observations). To study the gold price volatility in India, six major cities were chosen. The cities chosen for the study are Bengaluru, Chennai, Delhi, Hyderabad, Kolkata and Mumbai. The daily gold price of chosen cities in India was expressed in Indian rupees.

The return on the gold price was calculated as the logged differences as mentioned in equation (4).

Where R_t is the daily return of gold price at time t. P_t denotes the price of gold per gram at time period t and P_t-1 denotes the price of gold per gram in the selected city at time period t-1. “Eviews 9.5” statistical software package was used for performing the econometric analysis. For analysing the data, descriptive statistics, Augmented Dickey-Fuller Test, LM ARCH test and PGARCH model were used.

Empirical Results

Descriptive Statistics

The descriptive statistics for the gold price for the selected cities in India (in INR) along with US gold price (in USD) are presented in Table 1.

Table 1: Gold Price (Per Gram) (From January 2011 To August 2017)
	Bengaluru	Chennai	Delhi	Hyderabad	Kolkata	Mumbai	US (in $)
MEAN	2636.872	2643.657	2639.375	2648.250	2640.253	2629.983	44.23502
MEDIAN	2675.500	2680.000	2674.000	2686.000	2676.000	2668.000	41.96476
MAX	3215.000	3205.000	3096.000	3125.000	3126.000	3177.000	60.92566
MIN	1833.000	1833.000	1833.000	1833.000	1833.000	1833.000	33.73899
STD. DEV	252.6705	254.0999	250.5639	256.6231	251.1132	250.6711	6.546049
SKEWNESS	-1.157965	-1.170757	-1.198153	-1.219037	-1.205242	-1.13512	0.602659
KURTOSIS	4.271804	4.445593	4.480392	4.439743	4.48474	4.372698	2.102491
JARQUE-BERA (Prob)	575.9340 (0.0000)	614.6290 (0.0000)	651.2364 (0.0000)	629.0054 (0.0000)	654.5494 (0.0000)	567.1600 (0.0000)	158.9288 (0.0000)

Source: Author?s calculation.

Table-1 shows the summary of statistics of the gold prices in the selected Indian cities and in the United States. The mean value of the gold price of all the six cities of India is around Rs. 2640/g. The maximum gold price during the study period was Rs. 3215/g observed in Bengaluru. Highest gold price observed in the US was $ 60.925/per gram. Among the Indian cities, Hyderabad had the largest standard deviation and Mumbai had the smallest standard deviation. The skewness for the Indian cities was all negative and for the US it was positive. As far as the kurtosis is concerned, for Indian cities, it was found to be around 4 and for the US it was around 2. The Jarque Bera test statistic for all the Indian cities and the US were significant at 5 percent level, indicating the fact that the gold price was not normally distributed.

Results of Augmented Dickey-Fuller Unit Root Test

Augmented Dickey-Fuller (ADF) Unit Root test was applied to the gold price returns of the chosen cities in India and of the US. This test was applied to examine the stationarity of the data. This test was necessary as non-stationary data will lead to incorrect conclusion (Dickey & Fuller, 1979). The null hypothesis of ADF unit root test is that the time series is non-stationary or it has a unit root. The observed t-statistics and the probability values of ADF unit root test are presented in table 2.

Table 2: Adf-Unit Root Test (At Level) Gold Price Return
Cities/US Gold price	t-Statistic	Prob.
BENGALURU	-52.51171	0.0001
CHENNAI	-51.52014	0.0001
DELHI	-37.75255	0.0000
HYDERABAD	-53.92193	0.0001
KOLKATA	-37.34143	0.0000
MUMBAI	-37.78904	0.0000
US	-41.81144	0.0000

The null hypothesis of non-stationarity was rejected for all the data series as all the calculated p values were less than 0.05, indicating the fact that the entire gold price returns data both in India and in the US were all stationary at level.

Estimation of Gold Price Volatility

PGARCH model was applied to the gold price returns of chosen cities in India to estimate the conditional variance. The presence of asymmetric effect and volatility clustering was also investigated. In order to test the impact of US gold price influence on the volatility, US gold price returns were introduced as a regressor in PGARCH equation for each of the cities. The model used in this study is shown in equation (5)

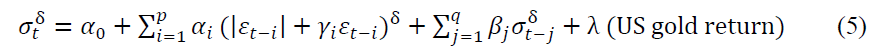
Where 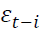is the lagged residual from the mean equation, 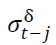is the lagged forecasted variance and 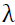is the coefficient measuring the impact of US gold price return on the volatility of gold prices in India.

GARCH family of conditional volatility models require appropriate mean equation specification (Bhattacharya, Sarkar, & Mukhopadhyay, 2003). Hence, the mean equation was estimated in an autoregressive form as given in equation (6).

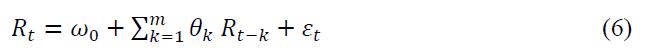
Where, 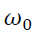is the constant, 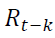is the lagged returns and 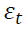is the residual. PGARCH coefficient estimates and their respective probability values are presented in Table 3.

Table 3: PGARCH Coefficient estimates
Cities	ARCH Term (αi)	Asymmetric Term(γ)	GARCH Term(β)	Power Term(δ)	US Gold Return(λ)
BENGALURU	0.085498 (0.0000)	-0.208602 (0.0000)	0.887923 (0.0000)	1.463871 (0.0000)	0.007027 (0.0160)
CHENNAI	0.069693 (0.0000)	-0.204044 (0.0000)	0.922061 (0.0000)	1.415292 (0.0000)	0.004618 (0.0062)
DELHI	0.1433898 (0.0000)	-0.067550 (0.1768)	0.707367 (0.0000)	1.660510 (0.0000)	-0.000185 (0.713)
HYDERABAD	0.200123 (0.0000)	-0.120086 (0.0069)	0.596259 (0.0000)	1.266926 (0.0000)	-0.030135 (0.0338)
KOLKATA	0.187155 (0.0000)	-0.092674 (0.0445)	0.671353 (0.0000)	1.512019 (0.0000)	0.007806 (0.032)
MUMBAI	0.099250 (0.0000)	-0.143746 (0.0006)	0.885414 (0.0000)	1.338543 (0.0000)	0.006970 (0.0267)

Source: Authors? calculation

Discussion

The ARCH 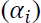and GARCH 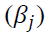coefficients were all significant at 5 percent level for the cities studied. Significant GARCH terms indicate the presence of volatility clustering in gold price volatility in India. Asymmetric 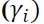coefficients for all the cities were significant at 5 percent level except for Delhi. This result supports the presence of leverage effect in gold price volatility. The estimated power transformation coefficients (δ) were ranging from 1.266 to 1.660 which is different from 2.

The 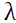coefficient which, estimates the impact of US gold price returns on the volatility of gold price in Indian cities were all significant at 5 percent level except Delhi. Hence, it can be inferred that US gold price returns significantly influence the gold price volatility in India.

ARCH LM tests were conducted on the residuals of the PGARCH equation to investigate the presence of autoregressive heteroskedasticity. The null hypothesis of this test is that the residuals from the PGARCH equation do not have the ARCH type of heteroskedasticity. If the residuals are free from autoregressive heteroskedasticity, it can be inferred that the PGARCH model fitted well on the data. The estimated coefficients (Obs*R-Squared) of the ARCH-LM test and its P values are presented in Table 4.

Table 4: Arch-Lm Estimates
Cities	Obs*R-Squared	Prob.
BENGALURU	6.436284	0.0112
CHENNAI	12.40135	0.0004
DELHI	0.467448	0.4942
HYDERABAD	0.792200	0.3734
KOLKATA	0.554439	0.4565
MUMBAI	7.226889	0.0072

The coefficients estimated for three out of six cities were significant at 5 percent level. The coefficients for the gold prices in Delhi, Hyderabad and Kolkata, were not significant, indicating the fact that PGARCH model fitted well for these cities and the residuals are free from ARCH type of heteroskedasticity.

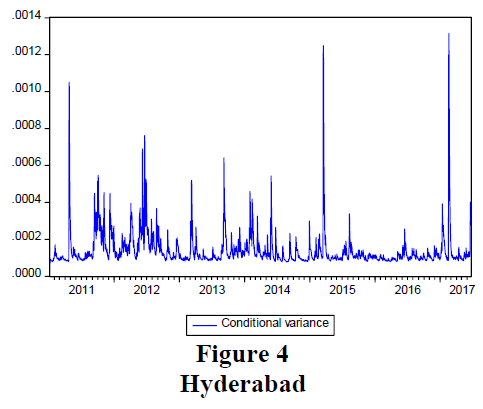
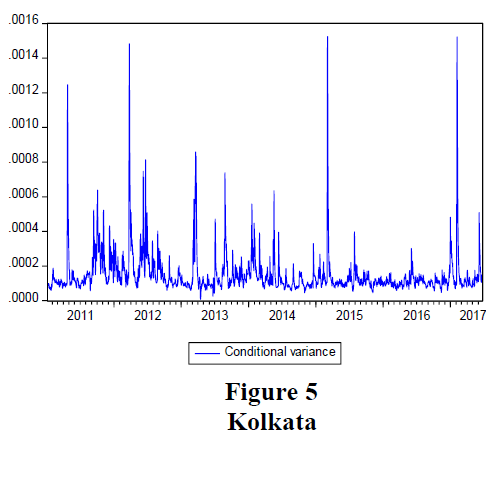
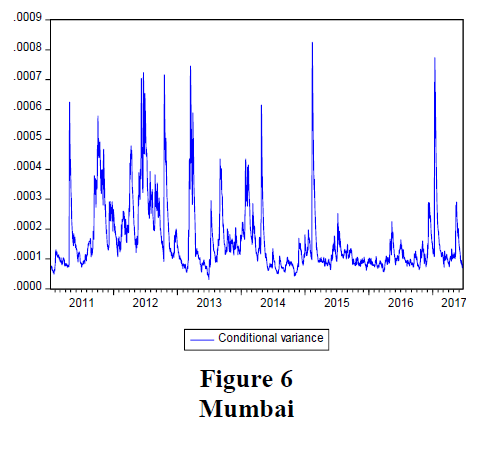
The conditional variance plots for all the six Indian cities are presented in Figures 1-6. These plots depict the features of the gold price volatility of the chosen cities over the study period.

It can be observed from figures 1 to 6, that from 2011 to of 2014 gold price in India was very volatile. The time period between 2015 to 2016 witnessed relative stability in the gold price in India. It can also be noticed that the conditional variance estimates were different between Indian cities and all of them were showing signs of volatility clustering.

Conclusion

This study was conducted by applying PGARCH model on the gold prices in India. This study was aimed at testing for the presence of leverage or asymmetric effect in the gold price volatility. Results of the variance estimation support the presence of leverage effect. Since the leverage effect is present, asymmetric conditional heteroskedasticity models are expected to perform better than symmetric models like GARCH. This study also investigated the possible impact of the US gold price on the volatility of gold prices in India. US gold price changes were found to influence the gold price volatility in almost all the cities analysed. Taking the support of all these results, it can be concluded that gold price volatility in India is indeed leveraged and the US gold price changes significantly influence the volatility of gold prices in India.

References

1. Bapna, I., Sood, V., Totala, N.K. & Saluja, H.S. (2012). Dynamics of macroeconomic variables affecting price innovation in gold: A relationship analysi. Pacific Business Review International, 1-10.
2. Bhattacharya, K., Sarkar, N. & Mukhopadhyay, D. (2003). Stability of the day of the week effect in return and in volatility at the indian capital market a garch approach with proper mean specification. Applied Financial Economics.
3. Bhunia, A. & Das, A. (2012). Association between gold prices and stock market returns: Empirical evidence from NSE. Journal of Exclusive Management Science.
4. Bollerslev, T. (1986). Generalized autoregressive conditonal heteroskedasticity. Journal of Econometrics, 307-327.
5. Christie-David, R., Chaudhry, M. & Koch, T.W. (2000). Do macroeconomics news releases affect. Journal of Economics and Business, 405-421.
6. Dickey, D.A. & Fuller, W.A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 427-431.
7. Ding, Z., Granger, C.W. & Engle, R.F. (1993). A long memory property of stock market returns and a new model. Journal of Empirical Finance (1), 83-106.
8. Engle, R. (2001). GARCH 101: The use of ARCH/GARCH models in applied econometrics. The Journal of Economic Perspectives, 15(4), 157-168.
9. Engle, R.F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. The Econometric Society, 987-1007.
10. Engle, R.F. & Patton, A.J. (2001). What good is a volatility model?
11. Gayathri, V. & Dhanabhakyam. (2014). Cointegration and causal relationship between gold price and nifty an empirical study. Abhinav International Monthly Refereed Journal of Research in Management & Technolog, 14-21.
12. Gencer, H.G. & Musoglu, Z. (2014). Volatility transmission and spillovers among gold, bonds and stocks: An empirical evidence from turkey. International Journal of Economics and Financial Issues, 705-713.
13. Glosten, L.R., Jagannathan, R. & Runkle, D.E. (1993). On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance, 1779-1801.
14. Ingalhalli, V., Poornima B.G. & Reddy, Y.V. (2016). A study on dynamic relationship between oil, gold, forex and stock markets in Indian context. Paradigm, 83-91.
15. Kalu, E. (2010). Modelling stock returns volatility in nigeria using GARCH models. Munich Personal RePEc Archive.
16. Miron, D. & Tudor, C. (2010). Asymmetric conditional volatility models: empirical estimation and comparison of forecasting accuracy. Romanian Journal of Economic Forecasting, 74.
17. Mishra, P.K. (2014). Gold price and capital market movement in India: The toda?yamamoto approach. Global Business Review, 37-45.
18. Mishra, P.K., Das, J.R. & Mishra, S.K. (2010). Gold price volatility and stock market returns in India. American Journal of Scientific Research, 47-55.
19. Narang, S. & Singh, R.P. (n.d.). Causal relationship between gold price and Sensex: A study in Indian context. Vivekananda Journal of Research, 33-37.
20. Singh, A. & Kaur, P. (2015). Stock market linkages: Evidence from the US, China and India during the subprime crisis. Timisoara Journal of Economics and Business, 137-162.
21. Singh, G. & Singh, P. (2010). Chinese and Indian stock market linkages with developed stock markets. Asian Journal of Finance & Accounting, 21-39.
22. Sjaastad, L. & Sacciavillani, F. (1996). The price of gold and the exchange rate. Journal of International Money and Finance, 879-897.
23. Srinivasan, P. (2014). Gold price, stock price and exchange rate nexus: The case of India. The Romanian Economic Journal, 77-94.
24. Toraman, C., Basarir, Ç. & Bayramoglu, M.F. (2011). Determination of factors affecting the price of gold: A study of MGARCH model . Business and Economics Research Journal, 37-50.
25. Tripath, L. Parashar, A. & Singh, R. (2014). Global factors & gold price in India - A causal study. International Journal of Advanced Research in Management and Social Sciences, 161-180.
26. Tripathi, V. & Seth, R. (2016). Market Efficiency, Inter-linkages and volatility transmission in stock markets of selected SAARC countries. South Asian Journal of management, 149.
27. Tully, E. & Lucey, B.M. (2007). A power GARCH examination of the gold market. Research in International Business and Finance 21, 316-325.
28. Worthington, A.C. & Pahlavani, M. (2006). Gold investment as an inflationary hedge: Co-integration evidence with allowance for endogenous structural break. University of Wollongong, 1-12.