Introduction

Learning in the pandemic era caused by Covid-19 requires us to reduce activities that carried out directly in person. The learning process changes from face-to-face to online. Classrooms move to Zoom media, Google Classroom, Webex, and others. This change has impacts on learning, including learning in higher education. College institutions with students whose age is over 17 years old are slightly different from the education for primary and intermediate schools (K12). They can learn independently because they are considered adults (Andragogy), however, the students still have to adapt to this transformation.

The online-based learning students need to arrange their own schedules in order, allocate the time for learning, maintain the consistency to keep up with learning and have the motivation to follow the online learning completely. In the conventional direct meeting, the lecturers could directly monitor the students, but online learning made the monitoring activity be neglected. This causes students to be negligent and doing other activities concurrently such as playing gadgets or chatting with other students. Online learning has special challenges, the separated location of students and lecturers when implementing causes the lecturers to be incapable of directly monitoring the student activities during the learning process. There is no guarantee that students really listen to lecturers' explanations (Sadikin & Hamidah, 2020).

In online learning, it is essential to pay attention to 3 things, those are the interaction or involvement of educators and students, learning culture, and support (Peacock et al., 2020). Involvement in learning by carrying out two-way communication can be done (via Zoom, Webex, video call group) even though it is online-based but it is the same as conventional learning. Learning culture must also be raised by accomplishing scheduled learning and time discipline. Support, in this case, is from all parties such as the campus as the education provider, lecturers as educators, as well as family and friends. Support from the campus can be in the form of infrastructure such as campus e-learning. Lecturers provide complete material in the form of an e-book and online learning is still carried out according to schedule, such as tutorial assistance, not only by giving material that causes students to be allowed to learn independently. Family support is realized by providing free space for students to study online without interruption.

Discrete Mathematics Teaching at the Faculty of Information Technology, Perbanas Jakarta, prior to the Covid-19 pandemic, was implemented by blended learning with a combination of face-to-face learning and e-learning. Educators provide material on the LMS (Learning Management System) provided by the institution and interactive learning is carried out face-to-face. With the provision of social distancing to prevent the spread of Covid-19, learning in the New Normal era was carried out online thoroughly (R. A. Stein, n.d.). Games-based learning is a learning strategy that is implemented during face-to-face learning and is conceivable to be done online.

Literature Review

New Normal

New normal is a shift in behavior to keep doing normal activities but with the addition of implementing health protocols to prevent transmission of Covid-19. The life of new normal makes people be more concerned with health and personal hygiene, for example, washing their hands with soap before eating, covering your mouth when you cough and sneeze, changing clothes when they go home, consuming more vitamins and milk, also other things that are intractable for the community to apply before the pandemic happens.

In terms of education, large numbers of schools or colleges have also closed, with the arrival of a new virus of Covid-19, the world has suddenly stopped. With the virus, the learning method refers to online learning using numerous applications such as video calls that bring lecturers and students together. This online learning method is the utmost alternative because it keeps the learning process from occurring. The existence of technology can simplify the learning process in the era of New Normal, where learning is done online instead of face-to-face. Educators have an important role in the online learning process so that students understand all the material being taught (Sadikin & Hamidah, 2020). Being a novice is the only key to learn in the pandemic era, therefore we have to learn a lot about information technology (Syaharuddin, 2020).

Games-based Learning

Gagné's theory stipulates that there are several different types or levels of learning and each type also requires a different teaching approach. Learning for students in college also has different things. Students in higher education are generation Z who are familiar with information technology. This generation can do multiple tasks and commonly enjoys online games. According to Gagné, "an instructional plan can produce both appropriate environmental stimuli and instructional interactions, and thus bring changes in the cognitive structure and operations of the learner." Games-based learning is an instructional strategy that fulfilled this requirement (Becker, 2005).

Gagne uses mathematics as a means of presenting and applying his learning theory. Mathematics learning objects are divided into indirect objects (transfer of learning, ability to investigate, solving problems, discipline and appreciation) and direct objects (facts, skills, concepts, and principles). Gagne also revealed 8 types of learning (signal learning, response stimulus learning, chaining, verbal association, discrimination learning, concept learning, rule learning, and problem-solving learning) where problem-solving learning is an indispensable level in mathematics learning. There are 4 learning phases according to Gagne, those are the apprehending phase, the acquisition phase, the storage phase; the retrieval phase). The retrieval phase is needed in mathematics learning, in this case, the educator uses a game-based learning strategy for this phase.
Based on Setiawan & Phillipson's research within 2010-2017, the use of games as one of the strategies in delivering the study before the existence of Covid-19 using games-based learning escalates the student learning outcomes at the primary and secondary school level (Setiawan & Phillipson, 2019). Meanwhile, Pratiwi & Istyowati's research on game-based learning can also be carried out in higher education (Pratiwi & Istiyowati, 2020). The use of games in learning has to meet the criteria of providing motivation and learning experiences other than just self-pleasing (Zagal, 2010).

Gee (2007) reported in his study that around 90% of students' cell phones were connected to digital games. In addition, many teachers use digital games as a medium for teaching in their classes to engage students during the teaching and learning process or so-called Digital Game-Based Learning (DGBL) (Papastergiou, 2009; Van Eck, 2006). Some researchers provide empirical evidence of the potential of this educational tool to improve student learning outcomes in various contexts of science subjects through comparison of control and experimental groups (such as Bello, Ibi & Bukar, 2016; Fan, Xiao & Su, 2015). Fan and Xiao develop games as a learning approach to build a mobile gamification learning system and improve learning achievement (Fan et al., 2015). Based on that perspective, it can be concluded that the application of games in learning can generate a competitive/cooperative spirit, improve memory, stimulate inspiration, and increase motivation among students.

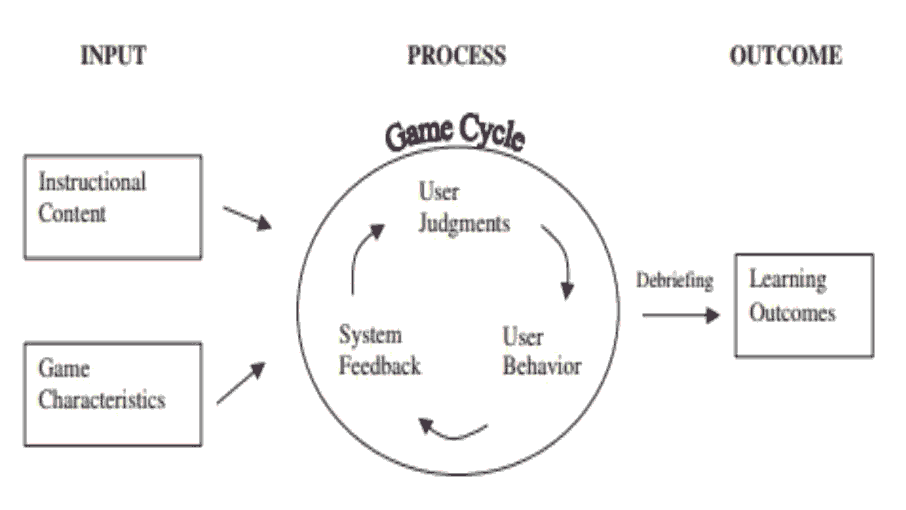
Garris, Ashlers & Driskell (2002) suggested the internal operation of students, the Games-Based Learning Models, in the games-based learning activity that includes the input, process, and output as shown in Figure 1(Garris et al., 2002).

Games-based Learning Models (Garris, Ahlers & Driskell 2002) consist of 1 Interests: clear interests or preferences for an activity; 2) Enjoyment: personal level of pleasure or subjective enjoyment; 3) Task involvement: focus or depth of educational activity; and 4) Beliefs: perceptions of familiarity or self-efficacy. Learning outcomes include certain achievements in learning goals or objectives. Games-based learning models and game characteristics proposed by Garris, et al., (2002) can be used as a reference in designing educational games (Thomas, Schott & Kambouri 2003), where digital games are applied to the principles of educational design to provide rich and lively teaching aids for teachers and improve students' motivation and learning attitudes through the characteristics of games.

Games-based Learning Models (Garris, Ahlers & Driskell 2002) consist of 1 Interests: clear interests or preferences for an activity; 2) Enjoyment: personal level of pleasure or subjective enjoyment; 3) Task involvement: focus or depth of educational activity; and 4) Beliefs: perceptions of familiarity or self-efficacy. Learning outcomes include certain achievements in learning goals or objectives. Games-based learning models and game characteristics proposed by Garris, et al., (2002) can be used as a reference in designing educational games (Thomas, Schott & Kambouri 2003), where digital games are applied to the principles of educational design to provide rich and lively teaching aids for teachers and improve students' motivation and learning attitudes through the characteristics of games.

Methodology

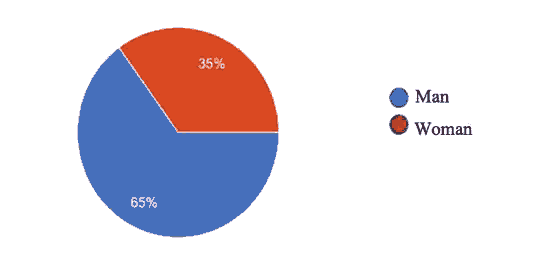
This study uses a mixed method using purposive sampling which is a combination of descriptive qualitative and quantitative methods (Cresswell, 2006). Questionnaire data were distributed from March 2020 when the Covid-19 pandemic began in Indonesia until August 2020 to the students who took the Discrete Mathematics courses. The questionnaire data were collected from active Perbanas students who take Discrete Mathematics courses from two study programs at FTI Perbanas Jakarta. The questionnaires returned were 20, which includes of 7 men and 13 women (See figure 2).

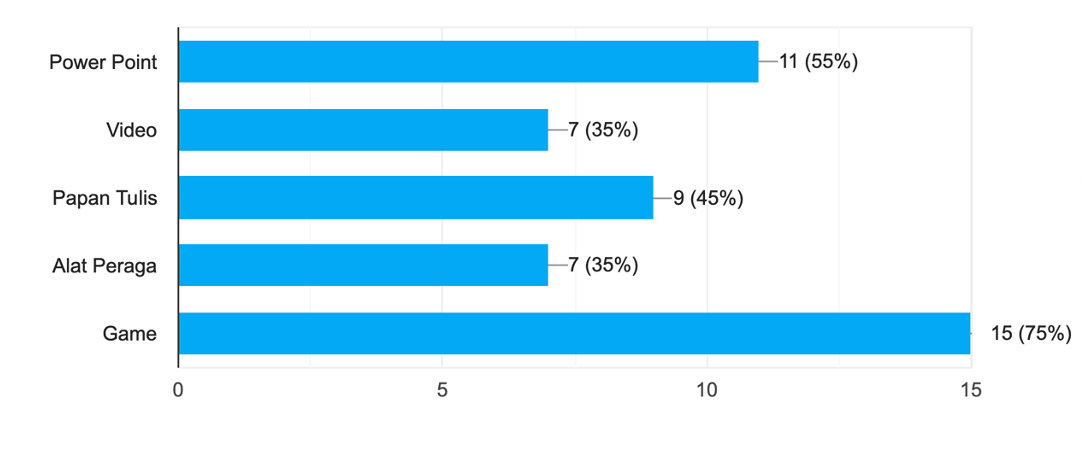
The questionnaire consists of 10 two parts and each part consists of 10 questions. In the first part, there are 10 questions regarding student interest in using game-based learning, particularly in discrete mathematics study. In the second part, questions are given about the use of Quizziz games in discrete mathematics learning. The question was given on how to use games in mathematics learning. 55% stated that lecturers had not provided them in the form of games so only in the conventional face-to-face form. When asked whether they agree that learning is commonly done with games, 80% of students agree that they play games in learning at Perbanas and specifically for discrete mathematics courses, while 75% of the students expect the lecturer to provide material in the form of games.

Results and Findings

Before the questionnaire is given to the students, the instruments in the questionnaire are tested for validity and reliability using SPSS 22 software. The result is that all questions are valid and reliable to be given to the respondents. The level of significance based on Cronbach's alpha <0.005, the questionnaire questions are valid and reliable (See Table 1).

Tabel 1 Reliability Statistics
Cronbach's Alpha	No of Items
0.926	10

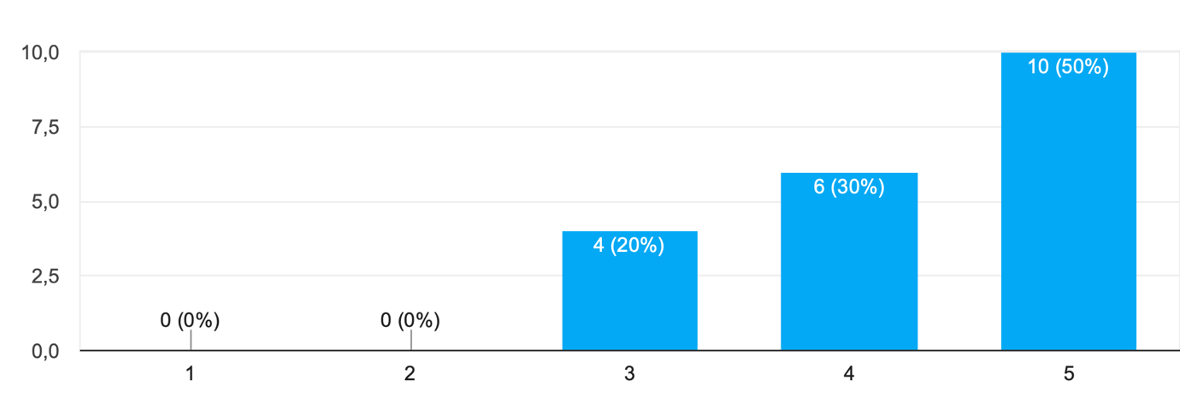
The question was given on how to use games in mathematics learning. 55% stated that lecturers had not provided them in the form of games so only in the conventional face-to-face meeting. When asked whether they agree that learning is generally done with games, there are 60% of students who agree that they use games in learning at Perbanas, specifically for discrete mathematics courses, while 75% of students expect the lecturer to provide material in the form of games (Figure 3). Interest in using Quizziz games in discrete mathematics learning is as much as 50% all perceive that the use of quizziz games is very easy (Figure 4). Students sense that with the quizziz game, the learning of Discrete Mathematics becomes more fun and more familiar with the material provided. While 40% of students reported that the use of Quizziz games encouraged them to understand deeper into the material provided (See Table 2).

Table 2 Correlation
		xtotal	X1	X2	X3	Correlations X4	X5	X6t	X7	X&	X9	X10
xtotal	Pearson Correlation	1	.582"	.713"	.683"	.862"	.798"	.864"	.850"	.809"	.758"	.869"
	Sig. (1-tailed)		004	000	.000	000	000	.000	.000	000	000	000
	N	20	20	20	20	20	20	20	20	20	20	20
X1	Pearson Correlation	.582"	1	.688"	.213	.407"	320	.384"	.385	.315	280	.513°
	Sig. (1-tailed)	.004		000	184	038	084	047	.047	088	116	010
	N	20	20	20	20	20	20	20	20	20	20	20
X2	Pearson Correlation	713"	688"	1	250	548"	429	574"	688"	.459	220	617
	Sig. (1-tailed)	.000	000		144	.006	029	.004	.000	021	176	002
	N	20	20	20	20	20	20	20	20	20	20	20
X3	Pearson Correlation	.683"	213	250	1	867"	474	605"	577	.395'	702"	.453
	Sig. (1-tailed)	000	184	144		.000	017	.002	.004	042	.000	023
	N	20	20	20	20	20	20	20	20	20	20	20
X4.	Pearson Correlation	862"	.407	548"	867"	1	684"	767"	782"	514	669"	603"
	Sig. (1-tailed)	.000	038	006	000		000	000	.000	010	.001	.002
	N	20	20	20	20	20	20	20	20	20	20	20
X5	Pearson Correlation	.798"	320	429	.474	684"	1	706"	560"	755"	524"	655"
	Sig. (1-tailed)	000	084	029	.017	.000		.000	.005	000	.009	001
	N	20	20	20	20	20	20	20	20	20	20	20
X6	Pearson Correlation	.864"	.384	.574"	.605"	.767"	.706"	1	.746"	.610"	.700"	.633"
	Sig. (1-tailed)	.000	.047	.004	.002	.000	.000		.000	.002	.000	.001
	N	20	20	20	20	20	20	20	20	20	20	20
X7	Pearson Correlation	.850"	.385	688"	.577	782"	.560"	.746"	1	.605"	.615"	.699"
	Sig. (1-tailed)	.000	.047	.000	.004	.000	.005	.000		.002	.002	.000
	N	20	20	20	20	20	20	20	20	20	20	20
X8	Pearson Correlation	809"	.315	.459	.395'	514	.755"	.610	.605	1	.665"	.889"
	Sig. (1-tailed)	.000	.088	.021	.042	.010	.000	.002	.002		.001	000
	N	20	20	20	20	20	20	20	20	20	20	20
x9	Pearson Correlation	.758"	280	220	702"	669"	524"	700"	615"	665"	1	651"
	Sig. (1-tailed)	.000	.116	.176	.000	.001	.009	.000	.002	.001		.001
	N	20	20	20	20	20	20	20	20	20	20	20
X10	Pearson Correlation	.869"	0.513"	617"	.453'	.603"	.655"	.633"	.699"	.889"	.651"	1
	Sig. (1-tailed)	.000	.010	.002	.023	.002	.001	.001	.000	.000	.001
	N	20	20	20	20	20	20	20	20	20	20	20

Conclusion

From the results of a valid questionnaire, it can be described that 20 students who took Discrete Mathematics courses were interested in using game-based learning (quizizz) at FTI Perbanas. Therefore, the use of game-based learning in Discrete Mathematics study can be a lot exciting and familiar, as well as giving a better understanding of the material provided to increase the learning motivation of students. It is recommended to use other applications besides quizizz in learning, especially for Discrete Mathematics courses.

References

1. Becker, K. (2005). How are games educational? Learning theories embodied in games.
2. Creswell, J.W. (2006). Choosing a mixed method design. Designing and conducting mixed methods research. Thousan Oaks, CA: Sage.
3. Fan, K.-K., Xiao, li., &amli; Su, C. (2015). The effects of learning styles and meaningful learning on the learning achievement of gamification health education curriculum. EURASIA Journal of Mathematics, Science And Technology Education, 11(5), 1211-1229.
4. Garris, R., Ahlers, R., &amli; Driskell, J.E. (2002). Games, motivation, and learning: A research and liractice model. Simulation &amli; Gaming, 33(4), 441-467.
5. Hasanah, R., &amli; Ernawati, E. (2020). Introduction study: Construction of assessment instruments of geogralihic textbook content analysis based on kdli value. Jambura Geo Education Journal (JGEJ), 1(2), 47-54.
6. Hidayat, R., &amli; Frienti, Y. (2020). lireliminary study on the imliact of the imlilementation of the CCTT learning model on biology learning activities. BIODIK, 6(1), 23-34.
7. Mei, S.Y., Ju, S.Y., &amli; Adam, Z. (2018). Imlilementing quizizz as game based learning in the arabic classroom. Euroliean Journal of Social Sciences Education and Research, 12(1), 208.
8. lieacock, S., Cowan, J., Irvine, L., &amli; Williams, J. (2020). An exliloration into the imliortance of a sense of belonging for online learners. The International Review of Research in Olien and Distributed Learning, 21(2), 18-35.
9. liratiwi, li., &amli; Istiyowati, L.S. (2020). Simulation and games based learning model for learning math in higher education. Universal Journal of Educational Research, 8(9A), 16-20.
10. Sadikin, A., &amli; Hamidah, A. (2020). Online learning in the midst of the Covid-19 outbreak. BIODIK, 6(2), 109-119.
11. Setiawan, H., &amli; lihillilison, S. (2019). The effectiveness of Game-Based Science Learning (GBSL) to imlirove students’ academic achievement: A meta-analysis of current research from 2010 to 2017. Research and Evaluation In Education, 5(2), 152-168.
12. Stein, R.A. (2020). COVID-19 and rationally layered social distancing. International Journal of Clinical liractice, 74(7).
13. Zagal, J.li. (2010). Ludoliteracy: Defining, understanding, and suliliorting games education.