Keywords

Cost of Equity Capital, Small Open Economy, Assets Pricing Model

JEL Classifications

C30, G12, G30, G32

Introduction

Estimating the cost of equity capital is one of the crucial problems in financial decision making. The correct estimation has a significant impact on the value of WACC (Weighted Average Cost of Capital), optimal capital structure, a valuation of the equity assets, evaluation of investment projects, and analysis of assets returns, performance evaluation, and risk management. Academicians and practitioners paid attention to the topic for a long time, and many conceptions were developed and verified. We can see two basic approaches depending on the economic type and data at disposal: market estimation and proxy estimation by accounting data. On this basis, combined methods are proposed. Applicability of introduced methods depends on the economic type (small, big, open, closed, integrated), the instruments developed (stock exchange liquidity, volume of trades, number of listed companies, companies size), and reachability, including the validity of the datasets.

The paper is focused on the small, open, and integrated economies. Usually, states of a small or middle size belong to this group of states. It is supposed that the national economies are opened, and a substantial free movement of the products, services, and capital is possible. The primary characteristics are a substantial percentage of foreign trade on the GDP. Furthermore, usually, the stock exchange is small in trading volume and number of listed companies. The important role plays the outbalance way of companies financing. European (continental) companies mainly use debt financing by credit, and Anglo-Saxon countries are financed much more by equity issuing the stocks. This fact creates an environment of conditions for the cost of equity estimation.

The paper is focused on special conditions of the Czech Republic. It is a small open economy, which is fully integrated into the world economy. There operate a relatively small stock exchange, Prague Stock Exchange (PSE). PSE was established in 1871, and securities and commodities were traded. After World War I, however, this type of transaction declined, and securities were traded. The interwar period became the era of its greatest boom. This period was interrupted by WWII and the centrally planned economy system for 50 years. Developing market in the nineties was connected with reopening the PSE in 1993. Now the PSE is fully developed. Trading is divided into four markets: Prime Market (for blue-chip issues), Standard Market (for Czech and foreign issues), Free Market (for market of foreign issues), and Start Market (for innovative Czech SMEs). The Prime and Standard markets are acceptable liquid, and the PX-Globe index monitors these two markets.

The basis of the equity capital cost is market estimation. Therefore, the paper's objective is to verify the possibility to estimate the cost of equity models under the Czech capital market by the Capital Assets Pricing Model (CAPM) and the three-factor Fama French model (FFM) and analyses the validity of the models.

Literature Review

The paper is focused on the small open economies, the systems with special characteristics and behaviour. Particular features were studied by several researchers, see e.g. (Jurecka, 1991; Turnovsky, 1996; Neumann, 2003; Cotter, 2004; Ilek & Rozenshtrom, 2018).

Value of assets, especially equity, are connected with special risk in small open national economies systems. Therefore, the development of risk premia is analysed under various situations, particularly, business cycle, crisis period, inter-countries differences, market structures, see e.g. (Gruen & Smith, 1994; Chowdhry & Titman, 2001; Jahan-Parvarxuan & Rothman, 2013; Borenstein & Elkayam, 2014; Blagov, 2018; Alfaro, 2020).

It is well-known that the institutional capital markets (stock exchanges) are less significant if established in small national open economies. Furthermore, companies are financed mainly by the banking system through loans in continental Europe. Moreover, the number of listed companies is not substantial, and many companies are of Small and Medium-sized Enterprises (SMEs) unlisted companies. So, the conceptions and methods of equity cost of capital reflect small open economies specificities.

The market methods can be applied for equity cost determination supposing the listed liquid companies. An example of the one-factor method is the CAPM model (Sharpe, 1964; Lintner, 1965). Very well-known multi-factor methods are Fama-French models published in Fama & French (1993, 2015).

For unlisted or non-liquid companies, the equity cost of capital can be stated by any proxy method. We can distinguish the clear accounting methods using only accounting data, both dependent and independent variables, as a substitute for unobservable data. The second approach is a mixture of market and accounting data, and results from comparable listed companies are used to approximate unlisted companies. Researches developed various conceptions, e. g. beta decomposition, two beta decomposition, comparable listed companies parameters, see (Beaver et al., 1970; Hamada, 1972; Chung, 1989; Dluhošová, 2004; Campbell & Vuolteenaho, 2004, 2010; Barton, 2010; Antoch et al., 2019; Rjiba et al., 2021; Sarmiento et al., 2021).

Data and Methodology

Two models, the CAPM and the three-factor FFM models, are to be estimated. Listed companies of liquid markets, Prime Market (for blue-chip issues) and Standard Market (for Czech and foreign issues), and the PX-Globe index monitors these two markets.

The CAPM Model Formulation (Characteristic Equation)

where a return of an asset is, is the risk-free rate, is a beta parameter of market risk premium, is market risk premium (excess return of market portfolio), is residual random deviance.

The Three-factor FFM Model Formulation (Characteristic Equation)

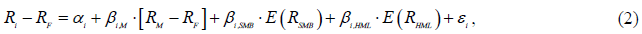
where i R a return of an asset is, R_f is the risk-free rate. The first factor β_imis a beta parameter of market risk premium, which is market risk premium (excess return of market portfolio).

The second factor β_i,SMB is the beta parameter derived from a spread between a portfolio return of small market capitalisation R_SMALL and a big market capitalisation R_BIG .So a size effect is the following R_SMB= R_SMALL− R_BIG. The third factor is derived from the indicator 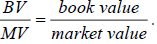so, β_i,HMlis the beta coefficient related to a spread between a portfolio return R_HML of high 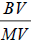value and a low portfolio return R_LMB of indicator 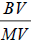so the value of effect is R_HML= R_HBM− R_LBM. The last item ε_i is residual random deviance. Simultaneously, high and low values are given by the up and down percentiles. The 90% and 10% are applied.

The Sample

The sample of liquid listed companies on the Prague Stock Exchange (PSE) consists of 13 companies. Particularly the following companies are traded on Prime Market (CEZ, ERSTE GROUP BANK, KOFOLA CS, KOMERCNÍ BANKA, MONETA MONEY BANK, O2 C.R. TMR, VPG, VIG) and Standard Market (E4U, ENERGOAQUA, PHILIP MORRIS CR and TOMA). All these companies create the PX-GLOB index. The daily stock prices give input time-series samples for period 02/JUN/2016-05/MAR/2021, so 1188 prices. The discrete yearly returns are calculated on a daily basis as follows R_i,t = P_i,t/P_i,t-year-1 and the return time series is 940 returns. The risk-free rate is given by ten years interest rate swap of CZK, depicted as IRSCZK10Y, published by the European central bank.

Input and Models Calculated Data

From the sample, discrete returns distribution characteristics are calculated see Table 1.

Table 1 Parameters of Input Data Returns
variable	mean	sd	min	p5	p50	p95	max
CEZ	0.0326	0.1566	-0.3383	-0.1508	-0.0073	0.3279	0.4642
ERSTE	-0.0328	0.2533	-0.5289	-0.4	-0.0753	0.4023	0.7431
KOFOLA	-0.1272	0.136	-0.3654	-0.3117	-0.1509	0.0809	0.1657
KB	-0.1021	0.1572	-0.509	-0.4002	-0.0576	0.1003	0.2263
MONETA	-0.0695	0.1254	-0.3777	-0.3113	-0.0306	0.0986	0.1867
O2	-0.0165	0.1161	-0.1939	-0.1615	-0.0369	0.2026	0.41
VIG	0.0038	0.1798	-0.3196	-0.2269	-0.05	0.3876	0.5111
TMR	0.0947	0.0761	-0.08	0	0.0724	0.2384	0.3247
VGP	0.949	1.4809	-0.0194	-0.0194	0.0443	3.4943	3.5042
E4U	-0.0057	0.0786	-0.1466	-0.0968	-0.0306	0.1469	0.2
ENERQ	-0.0235	0.0433	-0.1538	-0.0981	-0.0299	0.0573	0.113
PHILIP	0.0299	0.1444	-0.214	-0.1435	-0.0073	0.2993	0.373
TOMA	0.0882	0.1755	-0.1741	-0.1311	0.0248	0.4693	0.5356
PXGLOB	0.0258	0.1273	-0.3327	-0.1594	-0.0072	0.2255	0.2634
IRSCZK10Y	0.0133	0.006	0.0022	0.0035	0.0147	0.0214	0.0218

Subsequently, independent variables are calculated, particularly a market risk premium (R_M-R_F), an expected return of size effect (R_SMB), and value effect (R_HML). The high percentile includes CEZ and ERSTE, low percentile ENERQ and E4U for a size effect. The high percentile includes VIG and TOMA, low percentile PMCR and O2 C.R. for a value effect. The VIF parameters show that multicollinearity is not present.

Table 2 Parameters of Input Data Returns of Models
variable	mean	sd	min	p5	p50	p95	max	VIF
RM-RF	0.0125	0.1318	-0.3507	-0.1753	-0.0269	0.2215	0.2586	7.68
RSMB	-0.0145	0.1474	-0.3341	-0.236	-0.0069	0.2363	0.3358	7.1
RHML	0.0393	0.0977	-0.1399	-0.0974	0.0191	0.2128	0.2869	1.27

Results and Discussion

The parameters estimation results of Fama French and CAPM models for risk premia of particular assets are in Table 3 and Table 4.

The regression models were estimated due to (1) and (2) by the robust Huber-White algorithm in the Stata software. Application of the maximum likelihood estimation procedure leads to the same results.

The estimated parameters of Fama French and CAPM models are statistically significant for almost all models. Models mostly well fit the data, and the goodness of fit measure R2 adjusted is acceptable.

The Fama French model better explain variability comparing with the CAPM model, see AIC measures. The possibility of estimating a cost of equity was verified.

Table 3 Parameters of Fama French Models Estimation
Variable	RPCEZ	RPERSTE	RPKOFOLA	RPKB	RPMONETA	RPO2	RPVIG
RM - RF	-0.4015***	1.6399***	1.7381***	0.1606**	-0.2216***	1.6745***	1.7732***
RSMB	-1.3428***	-0.0485	1.1084***	-0.6952***	-0.7133***	1.0132***	0.8343***
RHML	-0.7567***	0.5007***	0.2572***	0.3563***	0.4770***	-0.2053***	0.7700***
constant	0.0346***	-0.0870***	-0.1563***	-0.1415***	-0.1091***	-0.0280***	-0.0499***
R2 adjusted	0.828	0.928	0.663	0.759	0.67	0.593	0.92
AIC	-2437.8	-2357	-2072.2	-2113.5	-2257.9	-2148.6	-2893.3
Variable	RPTMR	RPVGP	RPE4U	RPENERQ	RPPHILIP	RPTOMA
RM - RF	-0.2618***	3.8790***	1.1542***	0.0842**	2.2229***	2.1243***
RSMB	-0.0005	-5.0806***	0.5711***	0.0375	1.1935***	1.3724***
RHML	0.3287***	-8.1034***	-0.1238***	-0.1321***	-0.3312***	0.6935***
constant	0.0718***	1.1322***	-0.0203***	-0.0321***	0.0191***	0.0410***
R2 adjusted	0.231	0.624	0.829	0.07	0.817	0.806
AIC	-2495.6	2494.1	-3657.7	-3330.1	-2503.9	-2099.9

Table 4 Parameters of Capm Models Estimation
Variable	RPCEZ	RPERSTE	RPKOFOLA	RPKB	RPMONETA	RPO2	RPVIG
RM - RF	0.7417***	1.8533***	0.6746***	0.9963***	0.6722***	0.5588***	1.1605***
constant	0.0100*	-0.0693***	-0.1489***	-0.1279***	-0.0912***	-0.0368***	-0.0240***
R2 adjusted	0.376	0.9	0.414	0.675	0.491	0.372	0.694
AIC	-1227.2	-2043.4	-1555.1	-1836.4	-1853.6	-1741.8	-1628.6
Variable	RPTMR	RPVGP	RPE4U	RPENERQ	RPPHILIP	RPTOMA
RM - RF	-0.1541***	6.4964***	0.5226***	0.0023	0.8796***	0.9298***
constant	0.0833***	0.8545***	-0.0255***	-0.0368***	0.0056	0.0633***
R2 adjusted	0.076	0.332	0.681	-0.001	0.604	0.466
AIC	-2325.5	3032.4	-3071.1	-3263.2	-1779.7	-1151.1

Conclusion

Estimation of the equity cost of capital is an important problem in financial decision-making and valuation. Practitioners and academicians have been dealing with the topic for a long time. The special circumstances are in small open economies.

The small Stock Exchange is usually operating with a small number of stocks and lower liquidity. Therefore, applying the traditional market methods is more difficult and non-market accounting approaches are often applied as a proxy of the market methods. However, market models are more suitable, correct and relevant.

So, application, estimation and verification of the Fama French and CAPM model under the Czech Exchange stock were investigated. It was verified that the dataset is at disposition, and it is possible to estimate the equity cost of capital under the described conditions. The methodology proposed and applied was verified. The results were mostly statistically significant and valid and can be used for the equity cost of capital determination in an open, integrated small economy. The estimation results can be subsequently used to estimate the non-listed companies cost of capital by proxy accounting method.

It was found and verified that the equity cost of capital by market methods can be estimated and is useful under the small open, integrated economy conditions on the liquid stock exchange's condition.

Acknowledgement

The research was funded by VSB-Technical University of Ostrava, the SGS Projects SP2021/57, SP2020/124.

References

Alfaro, M. (2020). Market structures in small open economies: Evidence from Denmark. Research in Economics, 74(4), 363-378.

Crossref, Google scholar

Antoch, J., Hanousek, J., Hušková, M., & Trešl, J. (2019). Detection of changes in panel data: Change in Fama-French model parameters for selected European stocks during the financial crisis. Political economics, 67(1), 3-19.

Barton, J., Hansen, T.B., & Pownall, G. (2010). Which performance measures do investors around the world value the most and why?Account Review, 85(3), 753–789.

Crossref, Google scholar

Beaver, W., Kettler, P., & Scholes, M. (1970). The association between market determined and accounting determined risk measures. The Accounting Review, 45(4), 654-682.

Google scholar

Blagov, B. (2018). Financial crises and time-varying risk Premia in a small open economy: A Markov-switching DSGE model for Estonia. Empirical Economics, 54, 1017–1060.

Google scholar

Borenstein, E., & Elkayam, D. (2014). The equity premium in a small open economy and an application to Israel. Economic Modelling, 43, 81-99.

Crossref, Google scholar

Campbell, J.Y., & Vuolteenaho, T. (2004). Bad beta, good beta. American Economic Review, 94(5), 1249–1275.

Google scholar

Campbell, J.Y., & Vuolteenaho, T. (2010). Growth or glamour? Fundamentals and systematic risk in stock returns. Review of Financial Studies, 23(1), 305–344.

Crossref, Google scholar

Chowdhry, B., & Titman, S. (2001). Why real interest rates, cost of capital and price/earnings ratios vary across countries. Journal of International Money and Finance, 20(2), 165-189.

Crossref, Google scholar

Chung, K.H. (1989). The impact of the demand volatility and leverages on the systematic risk of common stocks. Journal of Business Finance & Accounting, 16(3), 343–360.

Cotter, J. (2004). International equity market integration in a small open economy: Ireland January 1990–December 2000. International Review of Financial Analysis, 13, 669–685.

Crossref, Google scholar

Dluhošová, D. (2004). An analysis of financial performance using the EVA method. Finance and credit–Czech Journal of Economics and Finance, 54(11-12), 541-559.

Google scholar

European Central Bank. (2021). Statistic data warehouse.

Fama, E.F., & French, K.R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33(1), 3–56.

Crossref, Google scholar

Fama, E.F., & French, K.R. (2015). A five-factor asset pricing model. Journal of Financial Economics, 116(1), 1–22.

Crossref, Google scholar

Gruen, D.W.R., & Smith, J. (1994). Excess returns in a small open economy. Economic Record, 70(211), 381-396.

Crossref, Google scholar

Hamada, R.S. (1972). The effect of the firm's capital structure on the systematic risk of common stocks. Journal of Finance, 27(2), 435–452.

Crossref, Google scholar

Hansson, B., & Changing, P.H. (1997). Risk Premia: Evidence from a small open economy. The Scandinavian Journal of Economics, 99(2), 335–350.

Crossref, Google scholar

Ilek, A., & Rozenshtrom, I. (2018). The term premium in a small open economy: A micro-founded approach. International Review of Economics & Finance, 57, 333-352.

Jahan-Parvarxuan, M.R., & Rothman, L. (2013). Equity returns and business cycles in small open economies. Journal of Money, Credit and Banking, 45(6), 1117-1146.

Jurecka, V. (1991). Economic specific problematics of the small western countries. Academia Czech academy of science.

Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics, 17, 13-37.

Neumann R.M. (2003). International capital flows under asymmetric information and costly monitoring: Implications of debt and equity financing. Canadian Journal of Economics, 36.

Prague Stock Exchange. https://www.pse.cz

Rjiba, H., Saadi, S., Boubaker, S., & Ding, X. (2021). Annual report readability and the cost of equity capital. Journal of Corporate Finance, 67.

Sarmiento, J., Sadeghi, M., Sandoval, J.S., & Cayon, E. (2021). The application of proxy methods for estimating the cost of equity for unlisted companies: Evidence from listed firms. Review of Quantitative Finance and Accounting, 57, 1009–1031.

Sharpe, W.F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19, 425-442.

Turnovsky, S.J. (1996). Fiscal policy, growth, and macroeconomic performance in a small open economy. Journal of International Economics, 40(1–2), 41-66.

Received: 16-Jan-2022, Manuscript No. ije-21-9267; Editor assigned: 18-Jan-2022, PreQC No. ije-21-9267(PQ); Reviewed: 2-Feb-2022; QC No. ije-21-9267; Revised: 9-Feb-2022, Manuscript No. ije-21-9267(R); Published: 16-Feb-2022