Keywords

Entrepreneurial regularities, Enterprise Numbers, Power Law, County GDP

Introduction

Compared to the late seventies, the mix and character of businesses in the United States had by 2007 changed dramatically (National Research Council, 2007). The U.S. economy had become
more integrated and globally interdependent and was much less reliant on the manufacturing sector because new technologies transformed the nature of work. These transformations resulted in a highly dynamic economy with outcomes varying over time by sector, region, and segment of society. The blurring of boundaries in the socioeconomic domain required that measuring business activity increasingly required tracking the connection between employers, employees, and independent entities (National Research Council, 2007). Longitudinal databases provided insight into these business dynamics and the operation of the U.S. economy. For instance, about one in seven jobs in the U.S. private sector had disappeared in an average year and much of job creation and destruction reflected business start-ups and shutdowns. The analysis of the National Research Council (2007), however, did not pay attention to proportionalities (regularities) and scaling phenomena in the demographic-socioeconomic-entrepreneurial nexus of U.S. cities and/or regions. This contribution considers this is necessary.

Early in the new millennium, researchers associated with the Santa Fe Institute in the U.S. initiated population-based scaling studies of cities (West, 2017). They reported that the functional properties of cities, such as their levels of conflict, economic productivity and material infrastructure vary in a scale invariant way from the largest cities to the smallest towns within an urban system (Bettencourt, Lobo & Youn, 2013). Even the smallest settlements have elements that functionally find correspondences in larger modern cities. Bettencourt (2013a) remarked that cities are first and foremost self-organizing social networks embedded in space and enabled by urban infrastructure and services. Bettencourt & West (2010) cautioned that the dynamics, growth and evolution of cities should be understood in scientifically predictable and quantitative ways.

Three questions arise from the foregoing:

• Do regions that include rural populations have similar characteristics than cities? Using power laws as ‘lenses’, Toerien (2020a) explored the demographic-socioeconomic interrelationships of U.S. counties as regional human settlements with mixed rural and urban populations. Extensive orderliness was detected and it was suggested that counties are also self-organizing networks. Regions with urban and rural populations seem to behave similarly to cities.

• Does the orderliness also pertain to the economic-entrepreneurial domain of regions? Based on the orderliness observed by Toerien (2020a) this is very likely but needs to be confirmed.

• Does a region with extensive geographic, demographic, climatic and other differences also exhibit such orderliness? The three questions provide the reasons for this investigation.

What region can be used to study these questions? Nobel Prize winning economist, Joseph Stiglitz, recently recommended: “I would encourage anyone interested in understanding the Great Depression or mid-19th century Britain to turn to Steinbeck or Dickens” (New York Times, 2020). Heeding Stiglitz’s advice and guided by James Michener’s book, Texas (Michener, 1985), the state of Texas was selected to examine the above questions. James Michener with the support of the then Governor of Texas, William Clements, spent 30 months researching Texas in order to produce his book. In his historical novel, he describes the many diverse influences that have shaped the state with its more than 250 counties. These include the impact of different ethnic and cultural groups such as Indians, Hispanics, Americans, Germans and others. These groups settled in and fought over the vast area of Texas in which the geomorphology and climate vary widely. The presence of oil, limited water resources in parts of the state and devastating storms have played their part in shaping the economy of Texas and the mindsets of Texans. Is it possible that against such a diverse background, order would presently prevail in its demographic-socioeconomic-entrepreneurial nexus?

The purpose of this contribution is to examine this question. If this is true, the economic-entrepreneurial orderliness in human settlements could be even more widely spread than previously believed. Bettencourt & West (2010) cautioned that the difference between ‘policy as usual’ and policy led by a new quantitative understanding of cities may well be the choice between creating a ‘planet of slums’ or finally achieving a sustainable, creative, prosperous, urbanized world expressing the best of the human spirit. This caution might have to be extended to include regions with urban and rural components, such as U.S. counties.

A null hypothesis was formulated:

H0: Despite the multi-dimensional diversity so evident in Texas, there is significant order in the demographic-socioeconomic-entrepreneurial domain of the counties of the state.

In order to examine the null hypothesis, the logic of the contribution is to:

1) Consider the economic and entrepreneurial orderliness that has been observed in cities and towns.

2) Consider the nature of entrepreneurship.

3) Consider power laws, the basic method by which such orderliness could be examined.

4) Describe the methods used in this contribution,

5) Present and discuss the results obtained.

Demographic and Socioeconomic Orderliness of Human Settlements

Cities are the crucible of human civilization, the drivers towards potential disaster, and the source of the solution to humanity’s problems (Bettencourt & West, 2010). These realities led researchers associated with the Santa Fe Institute in the U.S early in the new millennium to initiate investigations of the properties of cities (West, 2017). They reported the presence of extraordinary regularities that revealed the underlying mechanisms, dynamics and structure common to all cities (Bettencourt, Lobo, Helbing, Kuhnert & West, 2007; Bettencourt & West, 2010; Bettencourt, 2013a, 2013b, 2013c; Bettencourt et al., 2013; West, 2017; Bettencourt, 2020; Bettencourt, Yang, Lobo, Kempes, Rybski & Hamilton, 2020; Sahasranaman & Bettencourt, 2021). Over the last few decades, and in disciplines as diverse as economics, geography and complex systems, a perspective has arisen proposing that many properties of cities are quantitatively predictable due to agglomeration or scaling effects (Bettencourt et al., 2013; Gomez-Lievano, Patterson-Lomba & Hausmann, 2016; Molinero & Thurner, 2021). The functional properties of cities, such as levels of conflict, economic productivity and material infrastructure all vary in a scale invariant way from the largest cities to the smallest towns within urban systems (Bettencourt et al., 2013).

Power law analyses (log-log regressions) have been instrumental in revealing orderliness in the underlying dynamics and structures of cities (Bettencourt et al., 2007; Bettencourt, 2013b, 2013c; Lobo, Bettencourt, Strumsky & West, 2013). The use of power laws in scaling analyses quantifies how measurable aggregate properties respond to changes in the size of a system (Lobo et al., 2013). The analytical punch of power laws stems from the observation that the response is often a simple, regular, and systematic function over a wide range of sizes, indicating that there are underlying generic constraints at work on the system as it develops. Power law analyses have been a powerful tool across a broad spectrum of science and technology research (e.g., Ball, 2005).

Most urban characteristics, Y_(t), follow an approximate population-based power-law scaling:

Y_(t) ~ Y₀N_(t)^β

where Y0 is a normalization constant, N(t) is the population size at time, t, and β is the scaling exponent (Bettencourt, Lobo, Strumsky & West, 2010; Molinero & Thurner, 2021). Cities are clearly more than the linear sum of their individual components and many different properties of cities, from patent production and personal income to electrical cable length, are power law functions that quantify scaling impacts associated with population size (West, 2017). The scaling (exponential) exponents, β, of city power laws fall into distinct universality classes: super-linear (β>1)), sub-linear (β<1)) or linear (β~ 1) (terms used by West, 2017). Some socioeconomic outputs increase faster than population size and thus exhibit increasing returns to scale. For instance, coefficients reflecting wealth creation and innovation have β ≈ 1.2>1. They scale super-linearly.

This is typical of open-ended complex systems (Ortman, Cabaniss, Sturm & Bettencourt, 2015). Larger cities can, therefore, be envisaged as environments where a larger number of social interactions can be supported and sustained per unit time. In turn, these generic dynamics are the basis for expanding economic and political organization, such as the division and coordination of labour, the specialization of knowledge, and the development of hierarchical political and civic institutions (Ortmann et al., 2015). These dynamics provide the basis for cities to be the gateways for ideas (Glaeser, 2011).

The exponential coefficients of power laws associated with infrastructure development in cities are generally less than unity. These sub-linear coefficients indicate economies of scale in larger cities. In other words, more populous cities require proportionately less infrastructure.

To prove complex demographic/socioeconomic diversity, it is initially necessary to establish if there is demographic and socioeconomic orderliness in the counties (as a form of human settlements) of an extremely diverse region such as Texas.

Entrepreneurship in Human Settlements

Can the levels of entrepreneurial activities, and hence entrepreneurship, also serve as the basis of power laws that express orderliness in human settlements? To explore this issue, the nature of entrepreneurship must first be considered.

Entrepreneurship is crucial for economic development because it sets and keeps the capitalist engine in motion (Schumpeter, 1942). It incessantly revolutionizes the economic structure from within by continuously destroying the old one and creating a new one. In common with other unit ideas such as leadership, entrepreneurship is, however, an elusive concept (Anderson & Starnawska, 2008). It is broad and wide-ranging; the boundaries are fuzzy and may incorporate a number of disciplinary approaches. Entrepreneurship is integrally related to variables of environment, structure, strategy, and leader personality (Miller, 1983). Anderson (2000) suggested that it is the creation and extraction of value from an environment. However, this definition is so broad as to be almost undefined (Anderson & Starnawska, 2008). Reynolds, Hay & Camo (1999) suggested it is any attempt at new venture or new business creation, such as self-employment, a new business organization or the expansion of an existing business, by an individual, a team of individuals, or an established business. The international Global Entrepreneurship Monitor (GEM) project uses the latter definition to assess the entrepreneurship capabilities of different countries (Bosma, Hill, Ionescu-Somers, Kelley, Levie & Tarnawa, 2020; Kelley, Brush, Corbett & Majbouri, 2020). The Harvard Business School defines entrepreneurship as the pursuit of opportunity beyond resources controlled (Eisenmann, 2013). The international Global Entrepreneurship Monitor (GEM) project defines it as any attempt at new venture or new business creation, such as self-employment, a new business organization or the expansion of an existing business, by an individual, a team of individuals, or an established business (Kelley et al., 2020). Entrepreneurship is, therefore, not defined in terms of only individual effort. A group of people could provide the entrepreneurship necessary to start a new business. The total number of enterprises in a human settlement is a measure the level of its total entrepreneurship.

Total entrepreneurship can be sub-divided in many ways. For instance, there are different types of entrepreneurs, e.g., traders, medical practitioners, financial experts, teachers, etc. Total entrepreneurship can also be divided into ‘new entrepreneurs’, i.e., persons that can successfully start enterprises of types that have not been present before in a specific settlement, and ‘existing entrepreneurs’, persons that found additional enterprises of types that are already present in the settlement. Entrepreneurship in the tradable sector has also received some attention.

The economic strength of countries depends partly on the expansion of their tradable sectors via exports (Hasanov, 2013; Hlatshwayo & Spence, 2014). Moretti (2013) related the importance of the traded sector, and hence entrepreneurship in this sector, to the generation of jobs and wealth.

The theoretical definition of tradable and non-tradable industries in local economies is based on the geographical ranges of their respective markets (Moretti & Thulin, 2013). The products and services of the traded sector, which include products and services of sectors such as agriculture, fishing, manufacturing and mining, sell in external (non-local) markets and are sources of monetary inflows into countries and communities (Moretti & Thulin, 2013). The non-tradable sector provides products and services intended mostly for local markets. This sector tends to circulate money in countries and communities and not to generate external monetary inflows.

The scene has been set for investigation of the null hypothesis. The further logic of this contribution is simple. The methods are presented, starting with an explanation of the strategy followed. Thereafter the results are presented and discussed. Finally, conclusions are drawn.

Methods

Selection of Region to Study

Texas, the largest state in the U.S., is in many respects very diverse. It has more than 250 counties that range from very small to very large, which would enable the detection of orderliness, if present. Texas counties, a form of human settlement, were selected for this investigation.

Detection of Orderliness in Entrepreneurship

The increasing aggregation of people in cities are posing major challenges to governments and other authorities and a range of studies have focused on the population-based dynamics of many characteristics of cities (West, 2017). Linear proportionalities were recorded between population numbers and the total number of enterprises, and hence total entrepreneurship, of 125 South African towns (Toerien & Seaman, 2012). In Metropolitan Statistical Areas (MSAs) of the United States, the number of enterprises, and hence, total entrepreneurship, is also linearly proportional to population numbers (Youn, Bettencourt, Lobo, Strumsky, Samaniego & West, 2016). The first step in the investigation is to establish if population-based orderliness is also present in Texas counties. Consequently, the population-based demographic and socioeconomic dynamics of these counties were examined.

The existence of proportionalities between total entrepreneurship and other constituents of entrepreneurship have previously been reported. For instance, the total entrepreneurship of South African towns (Toerien & Seaman, 2014) and United States counties (Toerien, 2018b; Toerien, 2020b), scale strongly super-linearly (β ≈ 1.4) with the number of the different enterprise types present. The focus of the investigation, therefore, shifted to the enterprise-based dynamics of the counties. Total entrepreneurship (measured as total enterprise numbers) was used as independent variable in regression analyses with other entrepreneurial characteristics.

Toerien & Seaman (2014) had distinguished between entrepreneurship focused on enterprise types not yet present in a location (here called new entrepreneurship) and entrepreneurship focused on enterprise types already present (here called existing entrepreneurship). In ecological literature, the terms species richness and species diversity are sometimes used interchangeably (Spellerberg & Fedor, 2003). These authors suggested that ‘species richness’ should be used to refer to the number of species and ‘species diversity’ should be retained as an expression or index of some relation between number of species and number of individuals. A similar problem is present in enterprise dynamics, i.e., differentiation between the number of different enterprise types and the number of enterprises. Toerien & Seaman (2014) suggested the term enterprise richness should be used to represent the number of enterprise types in South African towns. That practice is followed here and enterprise richness serves as a measure of new entrepreneurship. The power law relationship between total number of enterprises (total entrepreneurship) and enterprise richness (new entrepreneurship) of the counties provides another test of entrepreneurial orderliness in the counties. From the foregoing it also follows that existing entrepreneurship equals total entrepreneurship minus new entrepreneurship. Consequently, there could also be proportionality between total entrepreneurship and existing entrepreneurship. A power law analysis between total entrepreneurship and existing entrepreneurship provides a further test of the presence of entrepreneurial orderliness in Texas counties.

Toerien & Seaman (2012) also provided evidence of many statistically significant relationships between total enterprise numbers and the enterprise numbers of different business sectors in South African towns. Therefore, the relationships between total entrepreneurship and entrepreneurship in 17 different business sectors of the Texas counties provided further tests of entrepreneurial orderliness in the counties. Given the importance attached to the tradable sector (Moretti, 2013) the relationship between total entrepreneurship and entrepreneurship in the tradable sector of Texas counties was also examined. This provided a further test of the null hypothesis.

Basic Data Sets

The investigation requires publicly-available data sets about U.S. counties. Three sources of information were used:

• The County Business Pattern (CBP) dataset is an annual series that provides U.S. subnational economic data by industry (U.S. Census Bureau, 2018). The dataset contains information about the numbers of the establishments (here called enterprises) and their employees for all U.S. counties. The CBP 2016 dataset is used in this investigation. Apart from the enterprise numbers and enterprise richness of the counties (i.e., the independent variables), the employment numbers associated with the enterprises and the number of enterprises in different business sectors (see below) were also extracted from the datasets.

• QuickFacts (U.S. Census Bureau, undated) provides socioeconomic information on U.S. counties. Information extracted from QuickFacts datasets includes: 1. Estimated county population in 2016, 2. Total county employment in 2016, 3. Total personal income (average personal income for a county multiplied by its population number), 4. The number of poor people (the percentage of officially poor people multiplied by the population number).

• The U.S. Bureau of Economic Affairs (2018) reported for the first time estimates of the gross domestic products (GDPs) for all U.S. counties. The dataset includes the total GDP as well as a breakdown of the GDP into GDPs for manufacturing, GDPs for services, and GDPs for government activities for each county. The 2015 dataset was used in this analysis.

Total Number of Enterprises, their Classification and Employment

For each Texas county, the total number of enterprises and the number of their employees were extracted from the dataset. The enterprises of each county were classified into 17 different business sectors on the basis of two-digit subdivisions (Table 1) of the six-digit classifications used in the North American Industry Classification System, NAICS (United States, 2017). The enterprises in each classification were enumerated. This process provided an estimate of the enterprise (and entrepreneurial) structure of each county.

Table 1 The Economic Sectors Based On First Two Numbers Of The Six-Digit North American Industrial Classification System (united states, 2017) Into Which All County Enterprises Were Classified Before Enumeration.
Sectors and numbers	Six-digit NAICS classifications starting with	Economic sectors
Non-tradable sector
1	22	Utilities
2	42,44,45	Wholesale trade & retail trade
3	48,49	Transport & warehousing
4	51	Information
5	52	Finance & insurance
6	53	Real estate and rental and leasing.
7	54,55	Professional, scientific, technical services & management of companies and enterprises
8	56	Administrative and support and waste management and remediation services
9	61	Educational services
10	62	Health care & social assistance
11	81	Other services
Tradable sector
12	11	Agriculture, forestry, fishing & hunting
13	21	Mining, quarrying, and oil and gas extraction
14	23	Construction
15	31,32,33	Manufacturing
16	71	Arts, entertainment, and recreation
17	72	Accommodation and food services

Enterprise Richness of the Counties

The six-digit NAICS system (United States, 2017) records the number of different six-digit classifications for a county and provides an estimate of its enterprise richness for the year under investigation. To avoid distortions as a result of an inadequacy of NAICS to truly record the enterprise richness levels of large counties (Toerien, 2020a), the Texas counties selected for use in a power law analysis of the relationship between enterprise numbers and enterprise richness levels were limited to 195 counties with enterprise richness levels between 30 and 325.
The Enterprise Numbers of the Tradable Sector of the Counties

Moretti & Thulin (2013) identified enterprises in the tradable sectors of European cities by assumption. They included agriculture, fishing, manufacturing, and extracting activities in the tradable sector. Services were included in the non-tradable sector. Broadly following this classification logic, the tradable economic sector of the Texas counties is here represented by subsectors 12 to 17 in Table 1. These sectors are the sources of external monetary inflows into the counties. The enterprise numbers in the tradable sector of the counties were derived by enumerating the enterprises in sectors 12 to 17.

Quantification of Relationships

The power law (log-log) relationships between the numbers of various characteristics were determined using MS Excel software.

Results

Demographic and Socioeconomic Orderliness

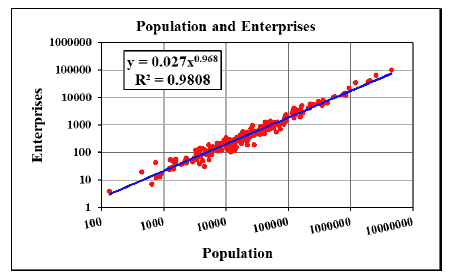
There is orderliness in the demographic-entrepreneurial domain of Texas counties as shown by a very high correlation between county population numbers and total entrepreneurship (Figure 1). Youn, et al., (2016) reported a linear relationship between metropolitan population numbers and establishments (enterprises). In Texas counties the relationship is a power law with a slightly sub-linear exponent (Figure 1). The power law extends over at least five orders of magnitude of both population size and total entrepreneurship.

Orderliness in the demographic-socioeconomic domain was further confirmed by power law analyses using population numbers as independent variable and some socioeconomic characteristics as dependent variables (Table 2). The results indicate extensive orderliness in the demographic-socioeconomic domain of the Texas counties.

Table 2 Population-Based Power Law Regularities In Texas Counties (Population Numbers Used As Independent Variable And Other Characteristics As Dependent Variables In Log-Log Regressions). GDP=Gross Domestic Product Of County; Total Entrepreneurship=Total Enterprise Numbers; R2 (%) Is Percentage Of Variation Explained, N=Number Of Counties In Comparison.
Characteristic	Correlation	R2 (%)	Exponent	n
Total entrepreneurship	0.96	96.2	0.968	253
Total county income	0.98	95.9	1.018	253
County GDP ($ million)	0.94	88.2	0.960	253
Degreed persons (no.)	0.98	96.5	1.095	253
Employment in county (no.)	0.97	95.0	1.123	253
Officially poor persons (no.)	0.98	96.5	0.979	253
Not poor persons (no.)	1.00	99.9	1.003	253

The enterprise dependency index, EDI, a measure of community prosperity/wealth (Toerien, 2018a), is determined by dividing population numbers by enterprise numbers. More people per enterprise indicate poorer communities, and vice versa. Community prosperity/poverty and entrepreneurship in Texas counties are associated with each other (Table 3). Surprisingly, more populous counties with higher levels of total entrepreneurship seem to overall have slightly poorer communities, possibly due to an influx of poor people. Conversely, in smaller counties the communities are slightly more prosperous.

Table 3 Enterprise Numbers And Population/Enterprise Ratios (= Enterprise Dependency Index, EDI) Projected For Different Population Numbers According To The Power Law Reported In Figure 1
Population	Enterprises	EDI (Population/enterprises)
2000	42	47.2
4000	83	48.3
8000	162	49.4
16000	317	50.5
32000	620	51.6
64000	1213	52.8

The information reported in Figure 1 and Tables 2 and 3 supports the null hypothesis.

Orderliness Based on Enterprise Numbers (Total Entrepreneurship)

Although orderliness based on population numbers was illustrated (Figure 1, Tables 1 and 2), there is a question if there is also orderliness when Texas counties are viewed through an ‘Entrepreneurial lens’. Three types of relationships based on entrepreneurship are examined.

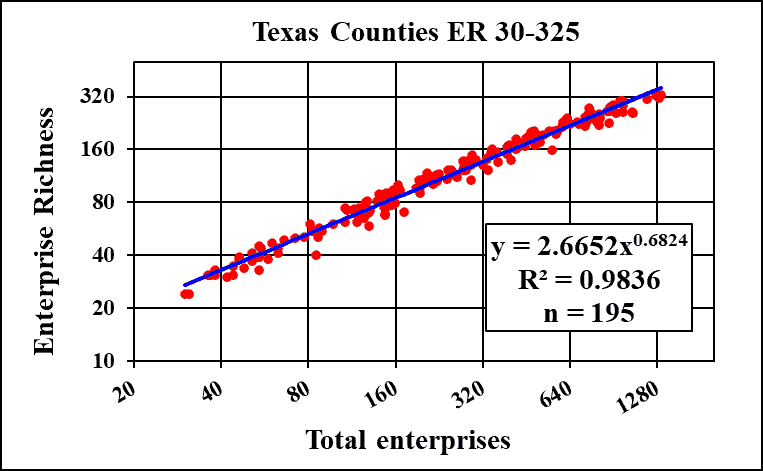
Firstly, there is a tight power law relationship with a sub-linear exponent between total entrepreneurship and new entrepreneurship in 195 Texas counties (Figure 2). The power law indicates that doubling (100 percent increase) of total entrepreneurship is associated with a 60 percent increase in new entrepreneurship. Just over 98% of the variation is explained as indicated by the high R² value in Figure 2. The converse (not shown) is also true. There is a super-linear power law relationship with an exponent of 1.44 between new entrepreneurship and total entrepreneurship. A doubling (100 percent increase) of new entrepreneurship in the Texas counties is associated with a 171% increase in total entrepreneurship. These analyses demonstrated extensive orderliness in these entrepreneurial characteristics.

Secondly, since existing entrepreneurship equals total entrepreneurship minus new entrepreneurship, the relationship between total entrepreneurship and existing entrepreneurship was also examined (Figure 3). There is also a tight power law relationship with a super-linear exponent between total entrepreneurship and existing entrepreneurship in the same 195 Texas counties. The power law indicates that every doubling (100 percent increase) of total entrepreneurship is associated with a 155 percent increase in existing entrepreneurship. Just over 99% of the variation is explained as indicated by the high R² value in Figure 3.

New entrepreneurship and existing entrepreneurship are quite differently associated with total entrepreneurship: the former with a sub-linear exponent and the latter with a super-linear exponent (Figures 2 and 3). Nevertheless, the multi-dimensional diversity of Texas described earlier, does not distort these manifestations of entrepreneurial orderliness in Texas counties. This provides further support for the null hypothesis.

Thirdly, orderliness has been demonstrated between total enterprise numbers and the number of enterprises in different business sectors of South African towns (Toerien & Seaman, 2012). The total enterprise numbers of Texas counties were divided into the number of enterprises in each of the enterprise sectors indicated in Table 1. When expressed as percentages of the total enterprise numbers in a county, it provides an estimate of the county enterprise structure. The relationships between total enterprise numbers (total entrepreneurship) and sector enterprise numbers have been examined for the Texas counties (Table 4). High correlation coefficients and R² values exceeding 85% in the relationships between total enterprise numbers and sector enterprise numbers for fourteen of the business sectors indicated extensive entrepreneurial orderliness (Table 4). Only three business sectors, i.e., mining and related activities; utilities; and agriculture and related activities, had lower correlations and R² values. Their relationships with total entrepreneurship were less orderly.

Table 4 Power Law (Log-Log) Relationships Between Total Enterprise Numbers (Total Entrepreneurship) And Enterprise Numbers In Different Business Sectors (Sector Entrepreneurship) (Described In Table 1). Counties without enterprises in a specific business sector were excluded in the sector analyses. R2 % is percentage variation explained, n=number of counties with enterprises in a specific sector
Business sector	Correlation	R2 %	Exponent	Constant	n
Real estate services	0.99	98.8	1.15	0.0138	229
Professional and scientific services	0.99	97.7	1.141	0.029	249
Health care & social assistance	0.99	97.8	1.129	0.0377	247
Administrative & support services	1	99.3	1.119	0.0146	238
Educational services	0.98	96.2	1.061	0.0051	173
Financial & insurance services	1	99.4	1.019	0.0567	250
Accommodation & food services	1	99.4	1.018	0.0821	250
Manufacturing	0.99	97.2	1.04	0.0261	233
Construction services	0.99	98.9	0.998	0.0857	249
Trade (retail & wholesale) services	1	99.2	0.981	0.235	251
Other services	1	99.5	0.942	0.1583	251
Arts & recreation services	0.98	96.7	0.921	0.0209	227
Information services	0.97	93.1	0.913	0.0289	235
Transport & warehousing services	0.94	87.6	0.854	0.1051	245
Mining, quarrying, gas & oil extraction	0.7	49.2	0.574	0.3488	226
Utilities	0.76	57.3	0.488	0.2247	241
Agriculture, Forestry, Fishing & Hunting	0.55	30.4	0.429	0.4268	186

The orderliness in the enterprise structures of the Texas counties is not uniform and the magnitudes of exponents of a number of the power law relationships between total enterprise numbers and sector enterprise numbers differ markedly (Table 4). Super-linear exponents were recorded for five of the business sectors (top shaded group in Table 4): i.e., real estate services, professional and scientific services, health care and social assistance, administrative and support services and educational services. Enterprise numbers of these sectors, and the respective entrepreneurship, are disproportionately higher in larger counties than in smaller counties.

Linear exponents were recorded for five other business sectors (top unshaded group in Table 4): i.e., financial and insurance services, accommodation and food services, manufacturing, construction services and trade services. The sector enterprise numbers, and the respective entrepreneurships, increase or decrease in step with total enterprise and population numbers because total county enterprise numbers are linearly related to county populations (Figure 1, Table 2).

Sub-linear coefficients were recorded for four business sectors (bottom shaded group in Table 4): i.e., other services, arts and recreation services, information services and transport and warehousing services. These business sectors are disproportionately higher in smaller counties.

Overall, the impacts of differently-sized exponential exponents on enterprise structures are relatively small. This is illustrated in Table 5 for six enterprise sectors: two with super-linear, two with linear, and two with sub-linear exponents.

Table 5 An Illustration Of The Impacts Of Differently Sized Power Law Exponents On The Enterprise Structures of Differently-Sized Texas Counties. The Power Laws In Table 3 Were Used To Calculate The Impacts
Business sector	Professional and scientific services (%)	Health care & social assistance (%)	Retailers & wholesalers (%)	Construction enterprises (%)	Information services (%)	Transport & warehousing (%)
Exponent	Super-linear	Super-linear	Linear	Linear	Sub-linear	Sub-linear
Value	1.141	1.129	0.981	0.998	0.913	0.854
Enterprises	Percentage of total enterprise numbers
200	6.4	7.8	22.3	8.9	1.9	5.1
800	7.9	9.5	22.1	9.0	1.7	4.2
1600	8.7	10.4	21.7	9.0	1.6	3.8
3200	9.5	11.3	21.2	8.9	1.5	3.4

Whereas the contributions to the enterprise structures of those sectors with either super-linear or sub-linear exponents, changed with a few percent between small (200 enterprises) and large (3200 enterprises) counties, the contributions of the sectors with linear exponents are large throughout. Consequently size-induced impacts on enterprise structures are limited and the overall orderliness in the entrepreneurial domain is not much affected. The results reported in this section are also in support of the null hypothesis.

There is also a strong power law relationship between total enterprise numbers (total entrepreneurship) and enterprise numbers in the tradable sector (entrepreneurship in the tradable sector) (Figure 4). The exponential exponent is slightly sub-linear. The enterprise numbers of the tradable sector are slightly disproportionately higher in smaller Texas counties than larger counties. These results are also in support of the null hypothesis.

Discussion

The National Research Council (2007) indicated a need to track the connection between employers, employees, and independent entities of human settlements. Despite evidence to the contrary (e.g., Bettencourt et al., 2007), the National Research Council did not pay attention to proportionalities (regularities) and scaling phenomena in the demographic-socioeconomic-entrepreneurial nexus of U.S. cities and/or regions. This prompted a question: is the entrepreneurial nature of Texas counties to a higher degree determined by scaling phenomena than by the historical, cultural and geographical diversity in Texas, which James Michener (Michener, 1985) sketched so vividly. This provided the primary reason for this investigation.

Researchers associated with the Santa Fe Institute in the U.S. have over the past two decades produced numerous publications that indicated that many of the functional properties of cities vary in a scale invariant way from the largest cities to the smallest towns within an urban system (e.g., Bettencourt, 2013a, 2013b, 2013c, 2020; Bettencourt et al., 2007, Bettencourt et al., 2013; West, 2017; Bettencourt et al., 2020; Sahasranaman & Bettencourt, 2021). Cities are self-organizing social networks embedded in space and enabled by urban infrastructure and services (Bettencourt, 2013c). In this contribution the population-based scaling studies of cities (West, 2017) was extended to examine aspects of the population-based dynamics of Texas counties. The recorded dynamics revealed that some of the functional properties of the counties also vary in a scale invariant way from the smallest to the largest counties. There is extensive orderliness (Figure 1, Table 2). The historical, cultural, climatic, geographical and climatic diversities of Texas (Michener, 1985) seem to be less important influencers of their socioeconomic dynamics. These observations supported the null hypothesis.

The interest in the orderliness of the socioeconomic-entrepreneurial nexus of Texas counties, prompted several different enterprise-based analyses. Firstly, a tight power law (log-log) relationship was recorded between total entrepreneurship and new entrepreneurship (Figure 2). The sub-linear exponent of the power law (0.68) is very similar to that (0.65) of Alabama counties Toerien, 2020b). It is also not very different from that (0.78) of South African towns (Toerien & Seaman, 2014). The converse, i.e., that there should also be a relationship between total entrepreneurship and existing entrepreneurship, was also demonstrated (Figure 3). In this case the exponent is super-linear (1.35).

The relationships of new entrepreneurship and existing entrepreneurship with total entrepreneurship differ markedly: large counties have many more enterprises founded based on existing entrepreneurship and fewer based on new entrepreneurship. Smaller counties are just the opposite. The entrepreneurial challenges of differently sized counties are distinctly different.

Secondly, similar to findings about South African towns (Toerien & Seaman, 2012) and despite the diversity of Texas, there is extensive order in the enterprise structures of Texas counties (Table 3). This is indicated by correlation coefficients close to unity for analyses that involved large numbers (> 200) of counties (Table 3). In only five of the enterprise sectors were sector enterprise numbers linearly associated with total enterprise numbers. Twelve were not. Non-linear order is, therefore, more prominent in the enterprise structures of the Texas counties. Four sectors have super-linear exponents and seven sectors have sub-linear exponents (Table 3).

This prompted a question whether the differences in the power law exponents could upset the orderliness that had been previously observed in the entrepreneurial domains of the Texas counties. An analysis of such a possibility (Table 4) indicated that the differences of exponents would not have a huge overall impact on the entrepreneurial orderliness.

Extensive orderliness was also detected between entrepreneurship in the tradable sector and total entrepreneurship (Figure 4). The power law with a slightly sub-linear exponent (0.964) extended over four orders of magnitude of total county enterprise numbers (a measure of total entrepreneurship). This is an important observation because entrepreneurship in the traded sector is a generator of jobs and wealth (Moretti, 2013). For instance, for each additional job in manufacturing in a given city, 1.6 jobs are created in the non-tradable sector in the same city (Moretti, 2010).

Based on all of the analyses (Figures 1-4, Tables 2 – 5), the null hypothesis that there is significant order in the entrepreneurial-socioeconomic domain of Texas counties despite the state’s multi-dimensional diversity (Michener, 1985) has been accepted. The demographic-socioeconomic-entrepreneurial system of Texas counties appears to be extremely robust.

A final comment deals with the nature of the null hypothesis. The statement on which it is based, is not frivolous. Bettencourt & West (2010) pointed out that cities are complex systems and therefore difficult to understand in isolation. They stated there is an urgent need for an integrated, quantitative, predictive, science-based understanding of the dynamics, growth and organization of human settlements, such as cities. With their colleagues, these researchers have shown that these general trends can be expressed as simple mathematical ‘laws’ (Bettencourt & West, 2010). This contribution demonstrates that there is also a complex and robust entrepreneurial system operating in Texas counties. This entrepreneurial system can also be described by simple mathematical laws.

Could the power laws recorded here be used to make predictions about the entrepreneurial dynamics of Texas counties? This issue touches upon whether one can deduce causality from correlations? Pearl and Mackenzie (2018) observed that statistics tells us that correlation is not causation. They suggested that this mantra should be changed to some correlations do imply causation. Mayer-Schönberger & Cukier (2014) observed that in a big data world, one does not have to be fixated on causality. Instead, one can discover patterns and correlations in data that offer novel and invaluable insights. The correlations may not tell one precisely why something is happening, but they alert one to the fact that it is happening. Kahneman (2011) suggested that even simple algorithms offer predictive potential. Many properties of cities are quantitatively predictable due to agglomeration or scaling effects (Bettencourt et al., 2013; Gomez-Lievano et al., 2016; Molinero & Thurner, 2021). The power laws of Figures 1 to 4 and Table 4, therefore, provide insight about the entrepreneurial system of Texas counties and could be used for predictive purposes.

Acknowledgement

The Centre for Environmental Management, University of the Free State, Bloemfontein provided administrative and research support. Alumnus services of the Massachusetts Institute of Technology provided online scholarly journal access. Jean le Roux provided technical assistance.

References

1. Anderson, A.R. (2000) Paradox in the periphery: An entrepreneurial reconception. Entrepreneurship and Regional Development, 12(2), 91–110.
2. Anderson, A.R., & Starnawska, M. (2008) Research practices in entrepreneurship: Problems of definition, description and meaning. International Journal of Entrepreneurship and Innovation, 9(4), 221 – 230.
3. Ball, P. (2005). Critical mass: How one thing leads to another. London: Arrow Books.
4. Bettencourt, L.M.A. (2013a). The Kind of Problem a city is. Santa Fe Institute Working Paper: 2013-03-008. Accessed at: https://www.santafe.edu/research/.../working.../the-kind-of-problem-a-city-
   Bettencourt, L.M.A. (2013b). The uses of Big Data in cities.
5. Bettencourt, L.M.A. (2013c). The origins of scaling. Science, 340(6139), 1438 – 1441. DOI: 10.1126/science.123582
6. Bettencourt, L.M.A. (2020). Urban growth and the emergent statistics of cities. Science Advances, 6(34): eaat8812.
7. DOI: 10.1126/sciadv.aat8812
8. Bettencourt, L.M.A., Lobo J., Helbing, D., Kühnert, C., & West G.B. (2007). Growth, innovation, scaling, and the pace of life in cities. PNAS, 104(17), 7301–7306.
9. Bettencourt, L.M.A., Lobo J., Strumsky, D., & West G.B. (2010) Urban scaling and its deviations: Revealing the structure of wealth, innovation and crime across cities. PLoS ONE, 5(11), e13541. oi:10.1371/journal. pone.0013541
10. Bettencourt, L.M.A., Lobo J., & Youn, H. (2013). The hypothesis of urban scaling: Formalization, implications and challenges. arXiv, 1301.5919 [physics.soc-ph]. 24 Jan 2013
11. Bettencourt, L.M.A., Yang, V.C., Lobo, J., Kempes, C.P., Rybski, D., & Hamilton, M.J. (2020). The interpretation of urban scaling analysis in time. Journal of the Royal Society Interface, 17, 20190846. http://dx.doi.org/10.1098/rsif. 2019.0846
12. Bettencourt, L., & West, G. (2010). A unified theory of urban living. Nature, 467(7318), 912-913.
13. Bosma, N., Hill, S., Ionescu-Somers, A., Kelley, D., Levie, J., & Tarnawa, A. (2020) Global Entrepreneurship Monitor 2019/2020 Global Report. London: Londan Business School.
14. Eisenmann, T.R. (2013). Entrepreneurship: A working definition. Harvard Business Review, January 10, 2013. Accessed at: https://hbr.org/2013/01/what-is-entrepreneurship
15. Glaeser E. (2011). Triumph of the city: How our greatest invention makes us richer, smarter, greener, healthier, and happier. Baltimore, MD: Penguin Press.
16. Gomez-Lievano, A., Patterson-Lomba, O., & Hausmann, R. (2016). Explaining the prevalence, scaling and variance of urban phenomena. arXiv:1604.07876v1 [physics.soc-ph] 26 Apr 2016.
17. Hasanov, F. (2013). Dutch disease and the Azerbaijan economy. Communist and Post-Communist Studies, 46(4), 463–480. doi:10.1016/j.postcomstud.2013.09.001
18. Hlatshwayo, S., & Spence, M. (2014). Demand and defective growth patterns: The role of the tradable and non-tradable sectors in an open economy. American Economic Review: Papers & Proceedings 104(5), 272–277. doi:10. 1257/aer.104.5.272Kahneman (2011)
19. Kahneman, D. (2011). Thinking, fast and slow. Kindle Edition. Amazon Digital Services LLC.
20. Kelley, D.J., Brush, C.G., Corbett, A.C., & Majbouri, M. (2020). Global Entrepreneurship Monitor 2019/2020 U.S. Report. Babson Park MA: Babson College.
21. Lobo J., Bettencourt., L.M.J., Strumsky, D., & West G.B. (2013). Urban scaling and the production function for cities. PLoS ONE, 8(3): e58407. doi:10.1371/journal.pone.0058407
22. Mayer-Schönberger, V., & Cukier, K. (2014). Big data: A revolution that will transform how we live, work and think. London: John Murray Publishers.
23. Miller, D. (1983). The correlates of entrepreneurship in three types of firms. Management Science, 29(7), 770-791.
24. Molinero, C., & Thurner, S. (2021). How the geometry of cities determines urban scaling laws. Journal of the Royal Society Interface 18: 20200705. doi.org/10.1098/rsif.2020.0705 25.
25. Moretti, E. (2010). Local multipliers. American Economic Review: Papers & Proceedings, 100(2), 1–7, doi.org/10. 1257/aer.100.2.373
26. Moretti, E. (2013). The new geography of jobs. Boston: Mariner Books
27. Moretti, E., & Thulin, P. (2013). Local multipliers and human capital in the United States and Sweden. Industrial and Corporate Change, 22(1), 339–362. doi.org/10.1093/icc/dts051
28. National Research Council. (2007). Understanding business dynamics: An integrated data system for America’s future. Washington, DC: The National Academies Press.
29. New York Times. (2020). The nobel-winning economist who wants you to read more fiction. Accessed on 15 April 2020 at: https://www.nytimes.com/2020/04/09/books/review/joseph-e-stiglitz-by-the-book-inter- view.html
30. Ortman, S.G., Cabaniss, A.H.F., Sturm, J.O., & Bettencourt, L.M.A. (2015). Settlement scaling and increasing returns in an ancient society. Science Advances, 1(1), e1400066 doi.org/10.1126/sciadv.1400066
31. Pearl, J., & Mackenzie, D. (2018). The book of why: The new science of cause and effect. New York: Basic Books.
32. Reynolds, P.D., Hay, M., & Camo, S.M. (1999). Global Entrepreneurship Monitor: 1999 Executive Report. Kansas City: Kauffman Center for Entrepreneurial Leadership.
33. Sahasranaman, A., & Bettencourt, L.M.A. (2021). Life between the city and the village: Scaling analysis of service access in Indian urban slums. World Development 142, 105435 doi.org: 0.1016/j.worlddev.2021.105435
34. Schumpeter, J.A. (1942). Capitalism, Socialism and Democracy, (Third Edition). New York: Harper.
35. Spellerberg, I.F., & Fedor, P.J. (2003). A tribute to Claude Shannon (1916–2001) and a plea for more rigorous use of species richness, species diversity and the ‘Shannon–Wiener’ index. Global Ecology and Biogeography, 12(3), 177–179. doi:10.1046/j.1466-822X.2003.00015.x
36. Toerien D.F. (2018a). Productive knowledge, poverty and the entrepreneurial challenges of South African towns. South African Journal of Science, 114(11/12), Art.#4765, 8 pages. https://doi.org/10.17159/sajs.2018/4765
37. Toerien, D.F. (2018b). Productive knowledge, scaling, enterprise richness and poverty in a group of small U.S. counties. Cogent Social Sciences 4, (1) doi.org/10.1080/23311886.2018.1560883
38. Toerien, D.F. (2020a). Power laws and the demographic-socioeconomic-entrepreneurial nexus of United States counties. In: Jaworski, J.A. (Ed.), Advances in Sociology Research, 32, 65-114, Nova Science Publishers: New York.
39. Toerien, D.F. (2020b). Disproportionate agglomeration and scaling in regional socioeconomic analyses: Alabama counties as a case study. Cogent Social Sciences, 6(1), 1817256. doi.org/10.1080/23311886.2020.1817256
40. Toerien, D.F., & Seaman, M.T. (2012). Proportionality in enterprise development of South African towns. South African Journal of Science, 108(5/6), 38–47.
41. Toerien, D.F., & Seaman, M.T. (2014). Enterprise richness as an important characteristic of South African towns. South African Journal of Science, 110(11/12), Art. #2014-0018, 9 pages. doi.org/10.1590/sajs.2014/ 20140018
42. United States. (2017). North American industry classification system. Washington: Executive office of the president.
43. U.S. Bureau of Economic Affairs. (2018). GDP by county. U.S. Bureau of Economic Affairs. Retrieved December 13, 2018, from https://www.bea.gov/data/gdp/gdp-county
44. U.S. Census Bureau. (2018). County business patterns (CBP). Retrieved June 23, 2018 from www.census.gov/ programs-surveys/cbp/data/datasets.html
45. U.S. Census Bureau (undated) QuickFacts. Accessed at: https://www.census.gov/quickfacts/fact/table/US/PST 045219
46. West G. (2017). Scale: The universal laws of life and death in organisms, cities and companies. London: Weidenfeld & Nicolson.
47. Youn H., Bettencourt L.M.A., Lobo J., Strumsky D., Samaniego H., & West G.B. (2016). Scaling and universality in urban economic diversification. Journal of the Royal Society Interface, 13, 20150937. dx.doi.org/10. 1098/rsif.2015.0937