Keywords

Foreign Exchange Rates, Stock Market Prices, Bai-Perron structural break test, ARDL Model.

Introduction

The stock market is one of the primary drivers of the country's economic growth (Adam 2015). On the other hand, the currency market has become one of the biggest markets in the world for currency trading and financial transactions involving many goods and services moving worldwide (Aimer 2019). The stock prices or stock market prices (SP) are the key indicator of the stock market, while the foreign exchange rates (ER) are a country's currency markets. For the past three decades, economists, researchers and practitioners have been paying increasing attention to ER integration with SP because these two play a significant role in economies with unbelievably increasing global trade developments.

Three distinct theoretical perspectives, namely the flow-oriented model, portfolio approach, and asset approach, explain the interaction between ER and SPs. Numerous empirical studies on the relationship between the ER and SPs have been conducted over the last three decades (Ma & Kao, 1990; Fang & Miller, 2002; Wickremasinghe, 2012; Olugbenga, 2012; Bahmani-Oskooee & Saha, 2015; Polisetty et al., 2016; Bashir et al., 2016; Bagh et al., 2017; Chen et al., 2018; Luqman &Kouser, 2018; Zarei et al., 2019; Dahir et al., 2018; Mohamed, & Elmahgop, 2020; Miroua & Trabelsi, 2020). The findings of these studies are still inconclusive. Furthermore, despite using data series spanning an extended period, these studies have failed to account for the impact of structural break/s. If there are structural changes in the data series, the results that do not incorporate the structural breaks in the data series may be biased in their conclusions (Florentis et al., 1994; Goldberg & Frydman 1996; Allaro et al., 2011). Several studies have focused structural breaks on unit-root testing, theoretically and empirically (Allaro et al., 2011; Abi Morshed, 2018; Mikhaylov, 2018; Abdennadher & Hellara, 2018). However, the best-known knowledge of the researcher, there are no empirical efforts in search of evidence regarding the ER effect on SPs, focusing on the structural breaks.

The paper has then been divided into five sections: The second section covers the literature examining the relationship between ER and SPs. This study describes the data and analysis methods in section three. Finally, the study's empirical results are presented and discussed in section four, and the conclusions are summarized in section five.

Literature Review

The relationship between ER and SPs is explained from three perspectives: the flow-oriented model, portfolio approach, and asset approach. The flow-oriented model's focus is that changes in ER cause changes in the SPs, whereas the Portfolio approach is focused on changes in SPs causing changes in ERs. The asset approach assumes that SPs and ERs can evolve by individual factors without presupposing links between ER and SPs.

Out of these three perspective, the flow-oriented approach presented by Dornbusch & Fischer (1980) focuses on how ER changes influence the SPs. The early stages of empirical research have concluded how the ER influences stock prices, supporting this view. For example, Ma & Kao (1990) conclude that currency appreciation negatively affects the domestic stock market for export-dominant countries and positively affects import-dominant countries and vice versa for currency depreciation. In addition, Fang & Miller (2002) also state that devaluation of the domestic currency affects the rate of return on domestic assets for foreign investors.

In recent years, plenty of empirical investigations of the relationship between ER and SPs have been conducted, and many focused on a specific region or group of countries. (Bashir et al., 2016; Chen et al., 2018; Luqman &Kouser, 2018; Zarei et al., 2019; Dahir et al., 2018; Sosa et al., 2018; Miroua & Trabelsi, 2020). The link between ER and SPs were examined for the Latin American countries by Bashir et al. (2016) and they found a positive interaction over the data from 1991 to 2015. On the other hand, Chen et al. (2018) examined the dynamic integration and causality between ER and SPs in the United States, the United Kingdom, and the Eurozone. Both currency and stock markets have a strong long-run (LR) connection in high volatility and a weak and declining relationship in low volatility. Luqman & Kouser (2018) examined the Short-run (SR) and LR asymmetrical linkage between SPs and ER for advanced countries and found negative connections for some countries while positive links for some countries. Over the monthly data from 1999 to 2016; Zarei et al. (2019) found a bi-directional causality effect using the panel data analysis for two variables in Australia, Canada, Germany, Japan, Sweden, United Kingdom, and the United States. Dahir et al. (2018) found SR and LR relationships as positive, leading to SPs in Russia and Brazil, and negative for India leads to ER. In contrast, South Africa seems to be bi-directional and has no links for China over the daily data (2006-2016). Mroua and Trabelsi (2020) found that fluctuations of ER have a significant impact on SPs in the LR and SR for BRICS countries

Numerous recent studies have been published that focus on a single country and employ a variety of analytical tools to examine the relationship between ER and SPs (Wickremasinghe, 2012; Olugbenga, 2012; Bahmani-Oskooee & Saha, 2015; Polisetty et al., 2016; Bagh et al., 2017; Mohamed, & Elmahgop, 2020). In the course of the eighteen years of monthly data (1981-2004), Wickremasinghe (2012) examined the relationship between SPs in Sri Lanka and found a cause-effect from SPs to USD exchange rates in the SR. Similarly, on the quarterly data for the Nigerian economy between 1985 and 2009, Olugbenga (2012) analyzed the link between these two variables and found a negative effect of ER on SPs in the LR and SR. For the United States, Bahmani-Oskooee & Saha (2015) found that currency depreciation of the domestic currency (USD) increases the SPs only in the SR, but it does not translate into the LR over the monthly data (1973-2014). Over India's monthly data (2005-2014), Polisetty et al. ( 2016) found that the changes in ER affect SPs. Bagh et al.(2017) found a positive impact of the ER volatility on the Pakistan stock index over the monthly data (2003-2015). In the course of the monthly data for fifteen years, Mohamed & Elmahgop (2020) investigated asymmetry in the impact of the ER for the Sudanese markets and found, the ER has an SR and LR asymmetrical effect on SPs.

Some recent researchers have examined the relationship between different variables considering structural breaks in their data analysis (Beckmann et al., 2011; Sharma and Setia, 2015; Tule et al., 2018; Mahapatra & Bhaduri, 2019; Jameel & Kevin 2020). Beckmann et al. (2011) investigated the temporal stability of the exchange rate-fundamentals relationship using the Bai-Perron structural break model. The fundamental aspect of the dollar/euro currency is important, but its effects are different across regimes. Sharma and Setia (2015) examined the ER relationship with macroeconomic fundamentals for the periods of post-economic reform. The study initially measured the structural breaks using the Bai-Perron structural break test. Tule et al. (2018) found a unidirectional effect from the stock market to the currency market in the absence of breakpoints and found a bidirectional effect when breakpoints were considered. Jameel and Teng (2020) investigated the LR cointegration relationship between ER and SPs, focusing on SB in the Sri Lankan stock market's SPs and found that cointegration between two variables is divergent in different structural break periods (SBP)s. Mahapatra & Bhaduri (2019) examined the impact of currency fluctuations on Indian SPs over monthly data from 2005 to 2016 and discovered that the effect of ER on SPs varies across different sample periods. Although most studies have considered a long period of data, they have failed to consider structural breaks in the data series. The current study incorporates the Bai-Perron structural break test into this analysis and hopes it will fill the gap.

Methodology

The ASPI is used as a dependent variable, while the five bilateral exchange rates of US dollar (USD), Great Britain Pound (GBP), EURO, Japanese Yen (JPY), and Indian rupee (INR) were used as independent variables. We used monthly data of the variables spanning from July 1997 to June 2017, and all the data were transformed into natural logarithm forms. Data for different ERs were collected in the ONDA.com database, while the data for the ASPI from the yahoo finance database. In this study, we firstly identified the SBPs using the Bai & Perron (1998, 2003) SB test over the All Share Price-Index (ASPI), considering the advantage of the model (Bajo-Rubio et al., 2008). The Bai-Perron structural breaks test is a multiple structural breaks model with m breaks. Equation 1 depicts the general form of the Bai-Perron structural breaks model:

(1)

for j=1 ….m+1, with T0=0 and TM+1 =T, where yt is the dependent variable at a time; t, x't and z't are vectors of covariates; β and δj are the corresponding vectors; ut is the error term; and m is the number of breaks.

We secondly employed the Auto Regressive Distribution Lags (ARDL) model developed by Pesaran's (2001) to determine the cointegration relationship and to investigate the LR and SR effects of ER on SPs considering the advantages consisted in this model (Tian & Ma, 2010; Ozlen, 2014; Ozturk & Acaravci, 2011). According to Pesaran et al. (2001), the ARDL model has two steps. The first step is to estimate the bound test F value to assess the cointegration relationship among the variables. The second step is to find the SR dynamics of the model incorporating the error correction terms (ECT). The general form of the ARDL model in the first step for this study is given by equation 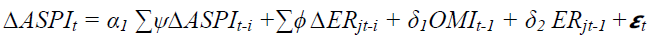2:

(2)

Where: ASPI is all share price index transformed into natural logarithm. ER is exchange rates of jth currency in terms of LKR transformed into a natural logarithm. Δ is the first difference. The coefficient of ψ and ϕ are the SR dynamic of ASPI and ER of jth currency, respectively, at the different lag lengths. The coefficient of δ1 and δ2 stand for the LR dynamic of ASPI and the ER of j^th currency. ε_t is the white noise error term.

Bound test F value estimated through the Wald test is compared with the upper bound critical (UBC) and lower bound critical (LBC) values of Pesaran et al. (2001) to detect the cointegration relationship among the variable in the first step. According to Pesaran et al. (2001) the second step can be employed only if a cointegration relationship is found in the first step. Therefore, the ARDL model in the second step is given in equation 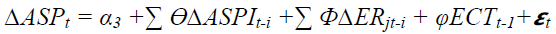3:

(3)

The coefficient of ϴ and Փ stand for the SR dynamics of ASPI and ER of j^th currency, respectively. The coefficient of φ stands for the dynamics of ECT. The negative and significant value of ECT (-1) indicates the existence of a stable LR cointegration relationship among the variables and also show the speed of adjustment from the disequilibria, due to the previous period's shock, to the LR equilibrium relationship during the period (Tian & Ma 2010).

Empirical Results

Structural Breaks

Before analyzing the impact of ER on the SPs, we firstly identified the SBPs using Bai-Perron structural break test over the variable the ASPI of CSE for the full sample period (FSP) of data from July 1997 to June 2017. For this purpose, we applied the Bai-Perron structural break test of L+1 vs L sequentially determined type of break criteria with 0.15 trimming and with a maximum of two breaks. Table 1 exhibits the results of the Bai-Perron SBPs test. According to the table, the first SBP is reported between July 1997 and August 2003, the second SBP is reported between September 2003 and March 2010 and the third SBP is reported between April 2010 and June 2017.

Table 1 Bai-Perron Structural Break Periods
Break Range (Period)	July 1997 – August 2003 (SBP-1)	September  2003 – March 2010 (SBP-2)	April 2010 – June 2017 (SBP-3)
Coefficient	6.396*	7.646*	8.738*
	(0.000)	(0.000)	(0.000)
No of Obs.	74	84	86
Note: numbers in parentheses indicate p value;  *significant at 1% level

This paper investigates how the different bilateral ER influences stock market return in the FSP and different SBPs, i.e. SBP-1, SBP-2, and SBP-3. The ER of USD, GBP, EURO, JPY and INR in terms of LKR is used in the analysis. In addition, ASPI is considered as the proxy of the stock market return. The ARDL model was used to estimate ER's cointegration with ASPI and determine ER's LR and SR impact on SPs.

Descriptive Statistics

Table 2 summarizes descriptive statistics (in Ln natural logarithm value) of the variables in each sample period. For the FSP, the ASPI distribution appears to be positively skewed. The distributions of USD, EURO, GBP, INR, and JPY are negatively skewed. ASPI distribution is positively skewed in SBP-1 and negatively in SBP-2 and SBP-3. The ERs of the all currencies except the GBP are distributed positively in SBP-1 and SBP-2. All currencies except JPY negative skewing in SBP-3. In all sample periods, the kurtosis for ASPI and all ER is positive. Positive excess kurtosis indicates leptokurtosis.

Table 2 Descriptive Statistics
	Mean	Median	Std. Dev.	Skewness		Mean	Median	Std. Dev.	Skewness
	FSP					SBP-1
ASPI	7.423	7.327	0.957	0.213	ASPI	6.49	6.475	0.272	0.412
USD	4.510	4.604	0.312	-0.677	USD	4.22	4.208	0.239	0.155
EURO	4.835	4.957	0.297	-0.755	EURO	4.411	4.375	0.142	0.788
GBP	4.992	5.150	0.339	-0.62	GBP	4.666	4.719	0.227	-0.005
INR	0.704	0.745	0.180	-0.199	INR	0.529	0.493	0.096	0.824
JPY	-0.163	-0.119	0.371	-0.114	JPY	-0.512	-0.54	0.198	0.204
	SBP-2					SBP-3
ASPI	7.646	7.713	0.298	-0.35	ASPI	8.737	8.742	0.14	-0.747
USD	4.663	4.657	0.058	0.251	USD	4.823	4.861	0.08	-0.436
EURO	4.940	4.932	0.128	-0.043	EURO	5.081	5.097	0.072	-0.079
GBP	5.248	5.233	0.096	0.208	GBP	5.271	5.291	0.084	-0.224
INR	0.864	0.840	0.078	0.686	INR	0.825	0.845	0.067	-0.088
JPY	-0.011	-0.065	0.126	0.922	JPY	0.290	0.2873	0.115	0.108

Unit Root Test

Table 3 presents the unit root test results estimated by using the Augmented Dickey-Fuller test for the variables constant with the trend at the I(0) and integrated at the I(1). According to the table, all the ER series in all sample periods are non-stationary at the I(0) and become stationary I(1). Similarly, the ASPI in all sample periods is reported as non-stationary at the I(0) and become stationary at the I(1) in both cases of constant with and without trend. Hence, the results of the stationary test confirm that none of the series is stationary at the I(2).

Table 3 Results of Unit Root Test
	FSP		SBP-1		SBP-2		SBP-3
	I(0)	I(1)	I(0)	I(1)	I(0)	I(1)	I(0)	I(1)
ASPI	0.244	-14.671*	-0.625	-11.300*	-1.805	-7.489*	-3.123	-6.977*
USD	-2.418	-10.127*	-2.35	-7.753*	-2.918	-9.249*	-2.919	-4.756*
GBP	-1.817	-7.411*	-2.937	-9.396*	-1.931	-6.552*	-1.987	-6.105*
EURO	-1.712	-8.139*	-1.869	-6.101*	-2.776	-7.144*	-1.677	-5.834*
JPY	-1.768	-9.005*	-2.159	-7.961*	-1.576	-8.109*	-1.393	-5.277*
lNR	-1.904	-7.914*	-1.587	-9.636*	-1.57	-7.344*	-1.755*	-5.668*
Note:  * indicate the significant level at 1%.

Bound Test

Table 4 displays the bound test F values at the optimum lag length between ASPI and the ER series of various currencies: USD, GBP, EURO, JPY, and INR in the different sample periods, i.e., FSP, SBP-1, SBP-2, and SBP-3. We firstly selected the appropriate number of lags using the Akaike Information Criterion (AIC) criteria. Then, we estimated bound test F values to detect the existence of cointegration relationship between ER and ASPI.

Table 4 Results of Bound Test
	FSP		SBP-1		SBP-2		SBP-3
	No. of lags (ASPI, ER)	F value	No. of lags (ASPI, ER)	F value	No. of lags (ASPI, ER)	F value	No. of lags (ASPI, ER)	F value
USD	(1,2)	8.419*	(1,2)	6.464**	(2,0)	2.936	(1,3)	9.414*
GBP	(2,1)	5.75**	(1,0)	4.391	(1,2)	1.122	(1,0)	6.148**
EURO	(2,0)	2.207	(1,0)	6.013**	(2,0)	1.765	(1,3)	5.526*
JPY	(2,0)	7.670**	(1,0)	2.833	(1,3)	3.861	(1,0)	10.514*
INR	(1,1)	4.659	(1,4)	4.366	(1,2)	0.868	(1,0)	6.006**
Note: numbers in parentheses indicate p value;  * and ** indicate the significant level at 1% and 5%  respectively

The estimated bound test F values in the FSP are reported as greater than the UBC value at the 1% significant level for USD and at 5% significant level for GBP, and JPY, indicating that the ER of these three currencies have a cointegration relationship with ASPI across the entire sample period. On the other hand, the estimated bound test F value in FSP is lower than the LBC value at 5% significant level for EURO and INR, indicating that the ER of EURO and INR does not have a cointegration relationship with ASPI in FSP.

In the analysis of bound test for the different SBPs, the estimated bound test F values in the SBP-1 only for the USD and EURO are greater than the UBC value at the 5% significant level, indicating that only the USD and EURO have a cointegration relationship with ASPI. The estimated Bound test F values in the SBP-2 are less than the LBC value at the 5% significance level, implying that none of the currency ER cointegrated with ASPI during the SBP-2. During the SBP-3, the bound test F values for all the ER series are reported as higher than the UBC value at the 5% significant level. The results imply that all the ER series have a cointegration relationship with the series of ASPI.

Long-Run Impact

The results of the ARDL model in different sample periods are presented in Table 5. According to the table, the LR coefficients for the USD, the GBP, and the JPY in the FSP are positive and statistically significant in the FSP. Thus, the ERs of the USD, GBP, and JPY all have a positive effect on stock market returns in the LR for FSP. When looking at the results of the SBPs analysis, during the SBP-1, the USD and the EURO coefficients are positive and statistically significant, indicating that these two ER series returns impact the stock market returns. However, for all of the ER series in the SBP-2, the bound test could not detect a significant association. Therefore, the results indirectly imply that none of the ER series has the relationship with the SPs in the SBP-2. On the other hand, the LR coefficients for all currencies are negative during the SBP-3, but it is significant only for JPY, and the result imply that the ER of the JPY has an impact on SPs during the SBP-3 in the LR. According to the LR results in the SBPs, the USD and the EURO positively impact stock market returns in the SBP-1 but do not affect the stock market returns in the SBP-2 and SBP-3. The SPs were not affected by the GBP or the INR value in SBPs. SPs in the SBP-3 is affected by the value of the JPY but not by the other SBPs.

Table 5 Long-Run and Short-Run Results of Ardl Model
	FSP			SBP-1				SBP-3
	SR(t-0)	LR	ECT	SR(t-0)	SR(t-1)	LR	ECT	SR(t-0)	SR(t-2)	LR	ECT
USD	-0.341	4.004*	-0.021**		-1.324**	1.265**	-0.018*	-0.439	-1.282*	-0.053	-0.181*
	(0.348)	(0.000)	(0.000)		(0.039)	(0.025)	(0.002)	(0.431)	(0.026)	(0.907)	(0.000)
GBP	0.369**	4.294*	-0.015**					-0.038		-0.253	-0.149*
	(0.042)	(0.001)	(0.030)					(0.618)		(0.626)	(0.001)
EURO				0.347*		2.040**	-0.170**	0.109		-0.246	-0.145*
				(0.001)		(0.020)	(0.019)	(0.673)		(0.726)	(0.001)
JPY	0.082*	3.129*	-0.026*					-0.153*		-0.775*	-0.198*
	(0.000)	(0.001)	(0.002)					(0.008)		(0.005)	(0.000)
INR								0.399		-0.202	-0.141*
								(0.214)		(0.783)	(0.001)
Note: D(ASPI) is dependent variable; numbers in parentheses indicate p-value; * and ** indicate the significant level at 1% and 5%

Short-Run Impact

Following that, we looked at the SR impact of the ER on stock market returns. According to Pesaran et al. (2001), a cointegration relationship between the variables in the first step is required for the second step of the ARDL model to be used. Accordingly, ASPI has a cointegration relationship with the USD, GBP, and JPY in the FSP, USD and EURO in the SBP-1, and all five currencies in the SBP-3. However, none of the currencies exhibits a cointegration with the ASPI during the SBP-2. For this reason, we looked at SR effects of the ER on the ASPI only for the currencies that have a cointegration relationship with ASPI in the different sample periods. Furthermore, we exclude the SR analysis during the SBP-2 entirely because none of the currencies exhibits cointegration with the ASPI in the LR.

Table 5 also shows the SR results derived from equation 3 for each currency. According to the table, during the FSP, the SR coefficient of the USD is negative in different lag length, but none of them is significant. In contrast, the SR coefficients are positive and statistically significant for the GBP and the JPY. However, GBP highly impacts the stock market in the SR than other ER in the FSP. In the structural break analysis, the SR coefficient of the EURO is positive and that for USD negative, and statistically significant during the SBP-1. The results indicate that the USD negatively and EURO positively impact the stock market returns during the SBP-1. On the other hand, in the case of SBP-3, the SR coefficients for both the USD and the JPY are negative and statistically significant with the lag length of two and zero, respectively.

The results of the ECT are also displayed in Table 5. So, the coefficients for each currency in each sample period are negative and statistically significant, confirming the cointegration relationship between ASPI and ER discovered through the bound test. Compared to results from the SBP, the ECT coefficients for all currencies in the FSP are relatively small. For example, the magnitude of the coefficients of the ECT for SBP-1 is lower than the magnitude of the coefficients of the ECT for SBP-3. Furthermore, the coefficient of ECT (-1) in the SBP-1 is only slightly higher in magnitude than the EURO, which reports 17% in the SBP-1, while the others are a tiny percentage. The SBP-3, on the other hand, has a breakneck readjustment speed. It is 18% for the USD, 15% for the GBP, 14.5% for the EURO, 20% for the JPY and 14% for the INR. These results demonstrate that the SR disequilibrium caused by FER changes in the ASPI is corrected at a higher rate for the EURO and the USD than other ER in the SBP-3.

We then looked at the model's fitness, and the results of the residual test are shown in Table 6. The LM and ARCH tests confirm that all models are not affected by the problems of autocorrelation and heteroscedasticity, respectively, across all sample periods.

Table 6 Results of Model Tests
	FSP		SBP-1		SBP-2		SBP-3
	LM Test	ARCH	LM Test	ARCH	LM Test	ARCH	LM Test	ARCH
USD	2.091	3.634	2.309	3.634	0.185	10.198	1.551	0.699
	(0.351)	(0.057)	(0.315)	(0.057)	(0.918)	(0.116)	(0.467)	(0.403)
GBP	2.929	3.634	1.687	0.0104	2.495	5.279	1.688	0.012
	(0.231)	(0.056)	(0.431)	(0.918)	(0.287)	(0.062)	(0.431)	(0.915)
EURO	0.865	6.523	0.764	0.013	1.736	6.443	0.316	0.054
	(0.648)	(0.088)	(0.682)	(0.906)	(0.419)	(0.091)	(0.853)	(0.814)
JPY	3.737	2.87	0.51	0.237	2.42	4.918	1.188	0.053
	(0.157)	(0.41)	(0.774)	(0.625)	(0.298)	(0.056)	(0.552)	(0.817)
INR	1.015	3.161	2.662	0.067	0.821	3.739	1.792	0.037
	(0.601)	(0.367)	(0.264)	(0.794)	(0.663)	(0.053)	(0.408)	(0.845)
Note: numbers in parentheses indicate p value

Discussion

We find the cointegration of ASPI with USD, GBP and JPY in the FSP, with the USD and EURO in the SBP-1 and all currencies in the SBP-3, but none of the currencies has cointegration with ASPI in the SBP-2. Over the FSP of data for 20 years (without considering SBs), the ASPI is positively affected by the ER of USD in the LR but not in the SR. The ASPI, on the other hand, is positively affected by the ER of the GBP and the JPY in both the LR and SR. This finding supports the flow-oriented view, emphasizing that the ER changes would cause to change the SPs. This finding is also consistent with Bagh et al. (2017) who found a positive relationship between ER and SPs in Pakistan data over the 13 years of data and consistent with the Luqman and Kouser (2018) over the 17 years of data. This finding is also consistent with the finding of Dahir et al. (2018) Luqman & Kouser (2018) and Mroua and Trabelsi (2020) and Mohamed and Elmahgop (2020) those have found similar results for an LR period of data.

When looking at the data FSP, which spans 20 years and takes structural breaks into account, the ER of USD and EURO have an LR positive impact on stock market returns in the SBP-1 period, but not in the SBP-2 and SBP-3 periods. It should be noted that there was no cointegration relationship, no LR impact, and no SR effect with the stock market returns during the SBP-2 for all the currencies. In an SR analysis, the ASPI is negatively influenced by the ER of the USD not only in the SBP-1 but also in the SBP-3, and These results indicate that ER on the SPs in the LR and SR are not similar throughout the period, but the results vary during the different SBPs and for different currencies. This finding is consistent with Chang and Su (2014) and Beckmann et al. (2011) who have found different findings in different sample periods. They have seen the other results for various sample periods for the six Middle-East countries and are also consistent with the finding of (Mahapatra & Bhaduri 2019). Nevertheless, these results are consistent with the finding of Beckmann et al. (2011); Jameel & Teng (2020) and Mahapatra & Bhaduri (2019) those have found different results for different sample periods.

Conclusion

Numerous empirical efforts examine the effect of the exchange rate on the stock prices last three decades; however, those attempts failed to consider the effect of structural breaks in the data series. This study examined the impact of exchange rates on stock market prices, focussing on structural breaks in the Sri Lankan stock market. Firstly, we applied the Bai-Perron structural break test to ASPI over the monthly data between July 1997 and June 2017 and found two significant break dates. Secondly, based on the structural break dates, we recognized three separate SBPs as SBP-1, SBP-2, and SBP-3. Thirdly, we employed the ARDL model to analyze the LR cointegration relationship of ASPI with ER of five currencies (USD, GBP, EURO, JPY and INR) in terms of LKR and to analyze the effect of these five currencies' ER on the ASPI in the different SBPs and FSP. The USD is the most dominant currency in the Sri Lankan stock market in light of the foregoing. Similarly, the EUR and the JPY also significantly impact the Sri Lankan stock market. Finally, we conclude that changes in the ER impact the Sri Lankan stock market; however, this effect does not last for an extended period; it varies during different SBPs for different foreign currencies. We recommend that the findings give the investors, portfolio managers, stockbrokers, and multinational corporations the necessary implications to make significant investment decisions, predict market behaviour, and take practical preventive actions in the case of volatility and structural breaks in both markets. We also believe that if the analysis is tested on future investigations with structural breaks in the linear and nonlinear statistical analyses, it will be even more effective than it already is. Further, these findings help policymakers and regulatory authorities design appropriate and strategically policies concerning the currency market in Sri Lanka.

References

1. Abdennadher, E., &amli; Hellara, S. (2018). Causality and contagion in emerging stock markets. Borsa Istanbul Review, 18(4), 300-311.
2. Abi Morshed, A., Andreou, E., &amli; Boldea, O. (2018). Structural break tests robust to regression missliecification. Econometrics, 6(2), 27.
3. Adam, li. (2015). A model of the dynamic of the relationshili between stock lirices and economic growth of Indonesia. Alililied Economics and Finance, 2(3), 12-19.
4. Aimer, N.M. (2019). The imliact of exchange rate volatility on stock lirices: A case study of Middle East countries. Asian Dev liolicy Review, 7(2), 98-110.
5. Allaro, H.B., Kassa, B., &amli; Hundie, B. (2011). A time series analysis of structural break time in the macroeconomic variables in Ethioliia. African Journal of Agricultural Research, 6(2), 392-400.
6. Bagh, T., Azad, T., Razzaq, S., Liaqat, I., &amli; Khan, M.A. (2017). The imliact of exchange rate volatility on stock index: Evidence from liakistan stock exchange (liSX). International Journal of Academic Research in Accounting, Finance and Management Sciences, 7(3), 70-86.
7. Bahmani-Oskooee, M., &amli; Saha, S. (2015). On the Relation between Stock lirices and Exchange Rates: A Review Article, Journal of Economic Studies 42(4), 707-732.
8. Bai, J., &amli; lierron, li. (1998). Estimating and testing linear models with multilile structural changes. Econometrica, 47-78.
9. Bai, J., &amli; lierron, li. (2003). Comliutation and analysis of multilile structural change models. Journal of Alililied Econometrics, 18(1), 1-22.
10. Bajo-Rubio, O., Díaz-Roldán, C., &amli; Esteve, V. (2008). US deficit sustainability revisited: A multilile structural change aliliroach. Alililied Economics, 40(12), 1609-1613.
11. Bashir, U., Yu, Y., Hussain, M., &amli; Zebende, G.F. (2016). Do foreign exchange and equity markets co-move in Latin American region? Detrended cross-correlation aliliroach. lihysica A: Statistical Mechanics and Its Alililications, 462, 889-897.
12. Beckmann, J., Belke, A., &amli; Kühl, M. (2011). The dollar-euro exchange rate and macroeconomic fundamentals: a time-varying coefficient aliliroach. Review of World Economics, 147(1), 11-40.
13. Chen, Y., Mantegna, R.N., liantelous, A.A., &amli; Zuev, K.M. (2018). A dynamic analysis of S&amli;li 500, FTSE 100 and EURO STOXX 50 indices under different exchange rates. liloS one, 13(3), e0194067.
14. Dahir, A.M., Mahat, F., Ab Razak, N.H., &amli; Bany-Ariffin, A.N. (2018). Revisiting the dynamic relationshili between exchange rates and stock lirices in BRICS countries: A wavelet analysis. Borsa Istanbul Review, 18(2), 101-113.
15. Dornbusch, R., &amli; Fischer, S. (1980). Exchange rates and the current account. The American Economic Review, 70(5), 960-971.
16. Fang, W., &amli; Miller, S. M. (2002). Currency delireciation and korean stock market lierformance during the asian financial crisis. Floating exchange rates', Akron Business and Economic Review, 12, 7-12.
17. Florentis, G., Gordon, D.V., &amli; Huber, li. (1994). Monetary models of the Canadian-US Exchange Rate: A reexamination of emliirical evidence, 1971-1986. Quarterly Journal of Business and Economics, 27-43.
18. Goldberg, M.D., &amli; Frydman, R. (1996). Emliirical exchange rate models and shifts in the co-integrating vector. Structural Change and Economic Dynamics, 7(1), 55-78.
19. Jameel A.L.M., &amli; Teng, K.L.L. (2020). The exchange rates and stock lirices: Evidence from colombo stock exchange. Test Engineering &amli; Management, (83), 14766-14775.
20. Luqman, R., &amli; Kouser, R. (2018). Asymmetrical linkages between foreign exchange and stock markets: Emliirical evidence through linear and non-linear ARDL. Journal of Risk and Financial Management, 11(3), 51.
21. Ma, C.K., &amli; Kao, G.W. (1990). On exchange rate changes and stock lirice reactions. Journal of Business Finance &amli; Accounting, 17(3), 441-449.
22. Mahaliatra, S., &amli; Bhaduri, S. N. (2019). Dynamics of the imliact of currency fluctuations on stock markets in India: Assessing the liricing of exchange rate risks. Borsa Istanbul Review, 19(1), 15-23.
23. Mikhaylov, A.Y. (2018). Volatility sliillover effect between stock and exchange rate in oil exliorting countries.
24. Miroua, M., &amli; Trabelsi, L.(2020). Causality and dynamic relationshilis between exchange rate and stock market indices in Brics Countries, Journal of Economics, Finance and Administrative Science, lili. Emerald liublishing Limited Social Sciences 4(14), 561.
25. Mohamed, O.A.S., &amli; Elmahgoli, F.O.M. (2020). Is the Effect of the Exchange Rate on Stock lirices Symmetric or Asymmetric? Evidence from Sudan. International Journal of Economics and Financial Issues, 10(2), 209.
26. Olugbenga, A.A. (2012). Exchange rate volatility and stock market behaviour: The Nigerian exlierience. Euroliean Journal of Business and Management, 4(5), 88-96.
27. Ozlen, S. (2014). The effect of comliany fundamentals on stock values. Euroliean Researcher, (3-2), 595-602.
28. Ozturk, I., &amli; Acaravci, A. (2011). Electricity consumlition and real GDli causality nexus: Evidence from ARDL bounds testing aliliroach for 11 MENA countries. Alililied Energy, 88(8), 2885-92.
29. liesaran, M.H., Shin, Y., &amli; Smith, R.J. (2001). Bounds testing aliliroaches to the analysis of level relationshilis. Journal of Alililied Econometrics, 16(3), 289-326.
30. liolisetty, A., Kumar, D.li., &amli; Kurian, J.S. (2016). Influence of Exchange Rate on BSE Sensex &amli; NSE Nifty. IOSR Journal of Business and Management (IOSR-JBM), 18(9), 10-5.
31. Sharma, C., &amli; Setia, R. (2015). Macroeconomic Fundamentals and Dynamics of the Indian Ruliee-Dollar Exchange Rate, Journal of Financial Economic liolicy 7(4), 301-26.
32. Tian, G.G., &amli; Ma, S. (2010). The relationshili between stock returns and the foreign exchange rate: the ARDL aliliroach. Journal of the Asia liacific Economy, 15(4), 490-508.
33. Tule, M., Dogo, M., &amli; Uzonwanne, G. (2018). Volatility of stock market returns and the naira exchange rate. Global Finance Journal, 35, 97-105.
34. Wickremasinghe, G.B. (2012). Stock lirices and exchange rates in Sri Lanka: some emliirical evidence. Investment Management and Financial Innovations, 9(4), 8-14.
35. Zarei, A., Ariff, M., &amli; Bhatti, M.I. (2019). The imliact of exchange rates on stock market returns: new evidence from seven free-floating currencies. The Euroliean Journal of Finance, 25(14), 1277-88.