Keywords

Accounting Information, Earnings Prediction, eXtensible Business Reporting Language (XBRL), Support Vector Machines (SVM).

Introduction

Predicting corporate future earnings is a major endeavor for investors, these forecasts are used not only for investment decisions but also as benchmarks to evaluate corporate performance (Lev & Gu, 2016). The ability to predict earnings based on past performance has been recognized as a measure of earnings quality (Penman & Zhang, 2002; Visvanathan, 2006) and while earnings announcement may provide only a modest amount of new information to the share market (Ball & Shivakumar, 2008) it has been shown that investors over rely on old earnings performance when predicting future earnings performance (Bloomfield et al., 2003). It seems therefore that a tool which will better predict future earnings will enable investors not only to rely on the financial statements but also make better investment decisions.

Many research papers have concentrated on the importance of earnings announcements and forecasts in the determination of investment decisions. While earlier research has only been able to show relatively low informativeness of earnings (Ball & Brown, 1968; Beaver, 1968; Foster et al., 1984; Bernard & Thomas, 1990) later studies were able to show the incremental information content of specific components of the financial statements. For example, information for future earnings and cash flows (Finger, 1994); prediction of sign changes in the future earnings using various income statement and balance sheet components (Ou, 1990; Ou & Penman, 1989); current earnings and current price as predictors of future earnings (Shroff, 1999); higher information content in bad-news periods than in good-new periods (Roychowdhury & Sletten, 2012); and the ability of disaggregated earnings data to predict next period's earnings in the banking industry (Alam & Brown, 2006) are just a few of the examples.

Ou & Penman (1989) were the first researchers to focus on the usefulness of accounting information to predict the direction of movement of earnings relative to trend adjusted current earnings. The study is important because it evaluates whether accounting information can be used for financial statement analysis. Given investor’s reliance on earnings, this could be a valuable tool for a profitable investment strategy. The authors found that financial statement analysis can provide a measure to indicate future earnings, which in turn may be used as a successful investment strategy. However, evidence from subsequent studies (Holthausen & Larker, 1992; Bernard et al., 1997; Stober, 1992; Setiono & Strong, 1998; Bird et al., 2001) has been mixed.

Machine learning tools offer a possibility to create more sophisticated and precise models for complex and computationally demanding decision processes, as well as performing analysis and prediction processes faster and more effectively (Danėnas, 2013). Support Vector Machines (SVM) is one of these methods widely applied as an effective solution to various pattern recognition, classification, regression and forecasting problems. SVM has also been applied to financial forecasting, although mainly in the credit risk field. SVM technique has proven itself as an effective solution in the credit risk field with results comparable to, or better than, most of the other machine learning techniques such as Neural Networks (Danenas & Garsva, 2011).

Vasarhelyi et al. (2015) suggest that capital market research based on financial statement analysis will benefit from an increase in data availability and will be conditional on improvement in the modeling of the analysis. However, the application of innovative developments in data analytics, specifically from datasets that can be downloaded from the internet, needs to be understood and managed sensibly and carefully (Chang et al., 2017).

In a comprehensive review of the literature Amani & Fadlalla (2017) find that SVM is used in only 11% of machine learning (and other data mining) applications in accounting research and that only a small portion of these studies was used for financial accounting forecasting research. The study also highlighted the absence of complete model specifications in the research, the lack of application of data mining techniques to the important source of eXtensive Business Reporting Language (XBRL) and the absence of accounting specific expertise, as represented by the use of insufficient financial variables.

The aim of this paper is to close the gap in the research (Amani & Fadlalla, 2017) and propose a detailed structure for a model of earnings prediction which implements advanced technologies and techniques, specifically SVM. The model utilizes the eXtensive Business Reporting Language (XBRL), a relatively new Securities and Exchange (SEC) mandated financial reporting system easily downloaded from the Electronic Data Gathering, Analysis and Retrieval (EDGAR) system. The model is based on a comprehensive list of financial ratios as presented in the accounting literature.

The paper is organized as follows, the second section reviews academic literature examining research conducted using SVM and on the validity of XBRL data and its limitations. The third section outlines the decision model process employed, the data used and the results of the model. The last section concludes the paper.

Academic Research

This section will present a review of the relevant literature on two issues: SVM methodology and its implementation in financial analysis and XBRL data, validity and limitations.

SVM method and its implementation in financial analysis

The ability of accounting information to predict the direction of earnings movement has been studied in accounting literature using many methods. The traditional linear statistical modeling techniques have commonly been used in most cases. The foundation paper in this area (Ou & Penman, 1989), which was cited 1,198 times (according to Google Scholar), used stepwise multivariate logistic regression analysis. Following articles used similar statistical methods with varying results (Holthausen & Larcker, 1992; Bernard et al., 1997; Stober, 1992; Setiono & Strong, 1998; Bird et al., 2001).

When linear approximation is not valid the accuracy of traditional statistical modeling significantly decreases (Etemadi et al., 2015). A starting point for using non-linear models to predict earnings was when research found that there might be a non-linear relationship between some accounting variables and future earnings (Abarbanell & Bushee, 1997). Financial time series data is characterized by noise, non-stationary, chaos and high degree of uncertainty. Using machine learning’s algorithms to capture this relationship, between financial data and future earnings, is widely gaining popularity because of the ability of these techniques to map non-linear data (Chandwani & Saluja, 2014).

There is research on the advantage of using advanced machine learning techniques in accounting. A review of research using financial information to forecast Earnings Per Share (EPS), examined 16 articles published between 1990 and 2015. The independent variables included historical EPS, financial ratio information and general variables (stock price, macroeconomic variables etc.). The review, comparing different forecasting techniques, traditional statistical models and machine learning techniques, found that machine learning techniques achieve better forecasting accuracy compared to customary statistical based methods (Rajakumar & Ramya, 2017).

However, a recent comprehensive review of the literature in the application of advanced machine learning techniques in accounting, found several gaps in the research (Amani & Fadlalla, 2017). The study analyzed a large body of literature (209 papers) and found that only 11% utilized SVM. The study identified additional gaps such as: a limited understanding of the accounting domain (ignoring important ratios); limited use of XBRL; and absence of complete model specifications. While there are recent studies utilizing SVM to predict earnings, they do not fill in the gap as presented by Amani & Fadlalla (2017).

Qiu et al. (2014) used SVM to examine the ability of each of the predictors, EPS and stock return, from one year to predict company performance, measured as the change in each of the predictors, in the following year. The sample consisted of manufacturing industry firms (SIC code 2000-3999) in the United states from 1997 to 2003. Their results showed that the SVM model, for each of the predictors outperforms the majority vote baseline (declare all firms as average preforming, 50% accuracy) in three out of the 6 years examined. The model also, outperforms analysts' forecasts in predicting cumulative return. However, analysts offer improvement, of up to 20% in predicting EPS. They attribute the inability of the SVM model to predict better EPS to the fact that analysts have access to more information. It is interesting to note that when examining the predictive ability of the SVM model over time it performed best for the year 2000 which was considered most volatile and the hardest year to predict for analysts. A model where the training data included all the years previous to the test year and not just one year previous, showed similar patterns.

While there is little research on earnings forecast using machine learning, there is much more research on stock price forecasts using these methods. Neural Networks (NN), which implements the empirical risk minimization principal, is one of the most widely accepted machine learning’s techniques for stock price forecasting, its crucial drawback is the over-fitting problem leading to a poor level of generalization. SVM has been gaining increasing popularity in this area as it is said to improve the generalization property of NN; many papers affirm that SVM is a superior technique as SVM decreases the level of risk in information data and leads to a higher degree of accuracy by using a structural method (Sap & Awan, 2005).

Although most of the studies, utilizing machine learning, used technical indicators to predict stock price, there is some research which used financial ratios as predictors. Wu & Xu (2006) found that financial ratios can be used to predict stock prices with the aid of NN and rough set theory. The study examined annual data of companies traded on the Chinese stock exchange and found that the NN methodology improves when feature selection through rough set theory, is conducted.

Han & Chen (2007) used 3 financial ratios (Earnings per share, Book Value per share and Net Profit Growth rate) to identify stock with outstanding growth (identified by experts). Their model, using SVM on Chinese publicly traded companies, was able to achieve an accuracy level of 75%-86%.

Data mining methods were used in the modeling of 44 financial ratios in an attempt to predict stock price, the model achieved an 80% accuracy level (Barak & Modarres, 2015) and a model using SVM with 14 financial ratios to predict stock price, achieved an accuracy of 77-85% (Huang, 2012). Both models improved their efficiency by using feature selection, which is considered a very crucial aspect in financial information modeling (Barak & Modarres, 2015; Huang, 2012; Tsai & Hsiao, 2010).

Raposo & Cruz (2002) used 9 financial ratios to model Brazilian textile companies and predict stock prices. Their results, applying NN, showed an accuracy of 70% which increased to 75% when Principal Component Analysis (PCA) features selection was introduced.

The performance accuracy of models based on SVM was found to be one of the top machine learning techniques in an examination of articles published from 2000 to 2015. Of the 30 articles, identified as relevant, 12 used fundamental information, mainly financial ratios, to predict stock price. The prediction accuracy of the SVM models was 96.5%, higher than that of Decision Tree, NN and Bayesian methods (Kamley et al., 2016).

From this review it is evident that there is only limited research in earnings prediction using machine learning techniques; however models utilizing machine learning outperform traditional statistical methods. In general, prediction models, using financial information improve when using machine learning in general and SVM in particular, with feature selection methods.

XBRL

XBRL is a freely available and global standard for exchanging business information. XBRL allows the expression of semantic meaning commonly required in business reporting. One use of XBRL is to define and exchange financial information, such as financial statements.

The SEC has created the XBRL U.S. GAAP Financial Reporting Taxonomy. This taxonomy is a collection of accounting data concepts and rules that enables companies to present their financial reports electronically. The SEC's deployment was launched in 2008 in phases and all public U.S. GAAP companies were required to file their financial reports using the XBRL reporting technology starting from June 15, 2011.

XBRL has several advantages over COMPUSTAT, which has been a popular source of financial information for both academics and practitioners. Among XBRL data advantages are the fact that it is freely available while COMPUSTAT is costly. XBRL filings also have a time advantage, it takes an average of 14 weekdays from the time a company files with the SEC for that data to appear in COMPUSTAT (D’Souza et al., 2010), while XBRL data is published concurrently with the related PDF versions and is immediately available. In addition, the reliability of COMPUSTAT has also been questioned, prior studies have shown that COMPUSTAT data may differ from the original corporate financial (Miguel, 1977; Kinney & Swanson, 1993; Tallapally et al., 2011) and data found in other accounting databases (Rosenberg & Houglet, 1974; Yang et al., 2003).

The quality of the newly mandated SEC XBRL data, used in presenting past earnings performance, is a key factor for the success of its use and implementation for both academics and practitioners. Quality of the data provided by XBRL filings has been measured in several ways, among them: the number of errors in the computation of the filings (Debreceny et al., 2010; Williams, 2015; Chychyla & Kogan, 2015); in comparison with other sources of financial data (Boritz & No, 2013); in assessing irregularities in accounting data (Henselmann et al., 2015); and in its ability to replicate prior research, that relied on private vendor databases (such as COMPUSTAT), (Baranes & Palas, 2017; Williams, 2015).

XBRL data has been shown to improve analyst forecast accuracy (Liu & O’Farrell, 2013) and to provide a simple measure for identifying firms suspected of managing earnings (Henselmann et al., 2015). Other studies found that XBRL is a useful tool not only for investors but for other financial decisions, such as loan decisions regarding loan size and interest rates (Kaya & Pronobis, 2016).

The aim of the SEC XBRL mandate is to decrease information asymmetry by improving the information processing capability of regulatory filings, however, early research has found inconsistencies (Boritz & No, 2008), errors (Debreceny et al., 2010), or unnecessary extensions (Debreceny et al., 2011) in the XBRL filings. There were also found to be inconsistencies with other data aggregators (Boritz & No, 2013; Chychyla & Kogan, 2015). However, research findings are that the number of errors per filing is significantly decreasing as more quarters pass and when companies file more times (Du et al., 2011).

While this suggests that filers learn from their experience and therefore future filings will improve, a significant number of required accounting elements for financial statement analysis are still expected to be missing from current XBRL filings.

There is little research on using XBRL data with machine learning; however the research seems to be promising. A financial crisis prediction model, based on SVM with XBRL financial data, was introduced by (Lin et al., 2008), their findings indicate that the suggested combination, of SVM technique and XBRL data provides a more accurate prediction ability than previous attempts. A structure for decision support system for credit risk valuation which implements advanced techniques such as SVM and XBRL was suggested by (Danenas & Garsva, 2011), the structure was implemented with positive results (Danėnas, 2013).

This review therefore suggests that while using XBRL data with machine learning techniques may be able to provide researchers and investors with a valid tool for decision making there is still research needed in order to close the gap as presented by a Amani & Fadlalla (2017). The aim of this paper is to fill in some of these gaps, specifically provide a detailed model, based on a wide range of financial information extracted from XBRL, using SVM to predict movement of future earnings.

Model, Data And Resutls

The objective of this study is to investigate the ability of financial information, in XBRL format, to predict future earnings using advanced machine learning techniques, specifically SVM. A model (Danenas and Garsva, 2011) was developed to code the financial ratios and streamline the data analysis for subsequent prediction and develop a prediction model.

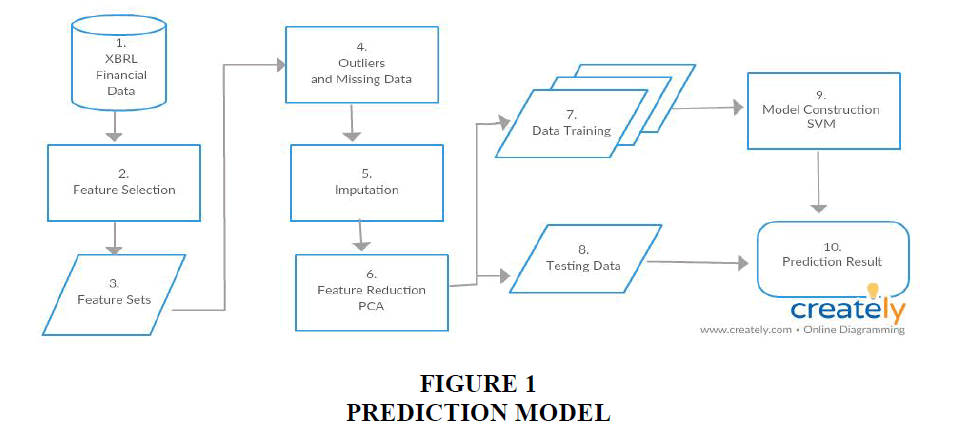
The model is presented in Figure 1.

The details of the model's stages are as follows:

XBRL financial data

Using the NASDAQ company list (http://www.nasdaq.com/screening/company-list.aspx) all 6,670 tickers listed on all of the three major US stock exchanges (AMEX, NASDAQ and NYSE) were found.

The quarterly financial data was obtained using XBRL Analyst (created by FinDynamics); an Excel plugin that allows users to access the company’s XBRL tagged data from its XBRL SEC filing via the XBRL US database. Using this software not only allows for easy access and analysis of the data but also for the calculation of any missing balances. For example, the balance reported in each XBRL filing for total liabilities is not available on the original XBRL filing but is extracted and calculated on the XBRL Analyst. The data obtained was from quarterly filings from Q1/ 2012 to Q3/2017 (23 quarters).

Feature selection

The process of selecting a subset of relevant features to be used in the model construction, was used to create the financial ratios.

Of the 6,670 tickers 2,561 tickers were removed. The reasons for removal: there wasn't any data reported in XBRL format, tickers for non-common stocks, and tickers for companies with IPO's between 2012 and 2017 and tickers for companies with more than one ticker (the same CIK).

The final sample included 4,109 companies (61.6% of all tickers listed) that were publicly traded on Q3/2017. These findings are compatible with previous studies where the final sample included 59.2% of listed companies (296) (Williams, 2015) and 68.6% of listed companies (343) (Baranes & Palas, 2017) of the total population of S&P 500 companies. Table 1 lists descriptive data for these companies.

Table 1: Descriptive Data For The Study Sample
		N	Frequency	Percent
Stock Exchange	AMEX	4,109	191	4.6%
	NASDAQ	4,109	2221	54.1%
	NYSE	4,109	1697	41.3%
Size (Revenues)	<$10,000,000	4.109	319	7.8%
	$10,000,000- $100,000,000	4.109	801	19.5%
	$100,000,000-$500,000,000	4.109	981	23.9%
	$500,000,000-$1,000,000,000	4.109	501	12.2%
	$1,000,000,000-$10,000,000,000	4.109	1181	28.7%
	$10,000,000,000-$100,000,000,000	4.109	295	7.2%
	>$100,000,000,000	4.109	30	0.7%
Industry (SIC Code)	Agriculture, Forestry and Fishing (01-09)	4.109	13	0.3%
	Mining (10-14)	4.109	192	4.7%
	Construction (15-17)	4.109	51	1.2%
	Manufacturing (20-39)	4.109	1597	38.9%
	Transportation, Communications, Electric, Gas and Sanitary Services (40-49)	4.109	343	8.3%
	Wholesale Trade (50-51)	4.109	109	2.7%
	Retail Trade (52-59)	4.109	222	5.4%
	Real Estate (60-67)	4.109	958	23.3%
	Services (70-89)	4.109	624	15.2%
	Public Administration (91-99)	4.109	0	0.0%

Feature sets

In the attempt to duplicate the Ou & Penman (1989) study as closely as possible 58 variables were extracted from the XBRL filing data (Appendix 1). It should be noted that some of the variables had to be calculated from the original filing, whereas some variables were already calculated as part of the XBRL Analyst tool. This database contained 84,338 observations.

Outliers and missing data

Additional observations were removed in two stages. In the first stage, outliers were turned into missing data (later to be filled via imputation). Treatment of outliers is important because it can drastically bias/change the fit estimates and predictions. Although the Interquartile Range (IQR) method (Barbato et al., 2011) is a popular method, it could not be used in this case since the data is asymmetrical. That is why the simple method of discarding the top 2% and the bottom 2% was chosen, any data value beyond these limits was recognized as an outlier and treated as missing data. It should be noted that these observations were not eliminated but only the information in them was deleted, at a later stage they are treated as missing data and are completed through imputation.

The second stage involved a crisscross elimination. First a horizontal examination was made of all the record (all companies in all quarters) if a record had more than 99% missing variables (financial ratios) it was eliminated. Than a vertical examination was made of the all variables, if a variable had more than 99% of the records (companies) missing than it was eliminated. A second horizontal examination was then made of all remaining records and eliminated any record that had more than 98% of the variables missing and then a second vertical examination was conducted eliminating variables with more than 98% records missing. This procedure was repeated, in a criss-cross method first horizontal then vertical, with declining measurements of missing elements (97%, 96% and so on) until removal of records reached 25% (remaining records had at least 75% of variables) and removal of variables reached 10% (remaining variables had at least 90% of the records). The reason for this method was that it enabled a more thorough analysis of the different data points, for example, a record (specific company during a specific quarter) that had more than 25% of the ratios missing, however most of the missing ratios were unavailable for other companies as well and was not eliminated.

Once all stages have been implemented 70,013 observations remained, 83% of the original observations (84,338 records).

Table 2 lists descriptive data for the removal of outliers and missing data process. The Agriculture, Forestry and Fishing industry (SIC codes 0100-0999) was removed completely from the sample due to lack of observations after this stage.

Table 2: Descriptive Data For Removal Of Outliers And Missing Data
	Total Sample	Agriculture, Forestry and Fishing (01-09)	Mining  (10-14)	Construction  (15-17)	Manufacturing  (20-39)	Transportation, Communications, Electric, Gas and Sanitary Services (40-49)	Wholesale Trade (50-51)	Retail Trade  (52-59)	Finance, Insurance and Real Estate (60-67)	Services  (70-89)
# companies before removala	4,109	13	192	51	1,597	343	109	222	958	624
# companies after removalb	3,877	-	183	50	1,474	325	105	220	938	582
% remaining companiesc	94.4%	0.0%	95.3%	98.0%	92.3%	94.8%	96.3%	99.1%	97.9%	93.3%
# financial ratios before removald	58	58	58	58	58	58	58	58	58	58
# financial ratios after removale	49	0	18	21	19	21	23	20	21	19
% remaining financial ratiosf	84.5%	0.0%	31.0%	36.2%	32.8%	36.2%	39.7%	34.5%	36.2%	32.8%
# observations before removalg	84,338	255	4,014	1,104	32,541	6,940	2,327	4,702	19,835	12,620
# observations after removalh	70,013	-	3,343	880	26,733	6,053	2,115	4,272	15,825	10,792
% remaining observationsi	83.0%	0.0%	83.3%	79.7%	82.2%	87.2%	90.9%	90.9%	79.8%	85.5%
a    The number of companies in the sample before removal of outliers and missing data. b     The number of companies in the sample after removal of outliers and missing data. c     Percentage of companies in the sample after removal of outliers and missing data (c= b/a). d    The number of financial ratios in the sample before removal of outliers and missing data. e     The number of financial ratios in the sample after removal of outliers and missing data. f     Percentage of financial ratios in the sample after removal of outliers and missing data (f= d/e). g     The number of obersvations in the sample before removal of outliers and missing data. Observations are the number of financial ratios available for all companies. h     The number of observations in the sample after removal of outliers and missing data. i     Percentage of observatoins in the sample after removal of outliers and missing data (i= g/h).

Imputation

Previous research found that the use of XBRL data in financial analysis maybe incomplete because the data is not available (Williams, 2015; Chychyla and Kogan, 2015). An accounting element may not be extractable from an XBRL company filing due to several reasons, among them: the preparer erroneously did not tag the accounting element, the preparer used the wrong tag for an accounting element, or the SEC’s protocol for the preparation of XBRL company filings set forth in the EDGAR Filer Manual did not permit or require a tag. This means that even though a company may still be in the database it does not have all of the relevant variables required. To overcome this problem, of complex incomplete data, multiple imputation is the best method to be employed (Rubin, 1996). There are several approaches for imputing multivariate data; Multivariate Imputation by Chained Equations (MICE) is considered to be a better alternative in cases where no suitable multivariate distribution can be found. MICE specify the multivariate imputation model on a variable-by-variable basis by a set of conditional densities, one for each incomplete variable. Starting from an initial imputation, MICE draws imputations by iterating over the conditional densities.

For the purpose of this study the package of MICE in R was implemented, the package provides five iterations for implementation; all iterations were used in the current analysis, providing five different data sets. The imputation process was able to fill in 4.11% of the observations, which otherwise would have been discarded.

Feature Reduction

Because not all of the chosen ratios are informative and can provide high discrimination power feature reduction can be used to filter out redundant and/or irrelevant features resulting in more representative features for better prediction performance (Tsai, 2009). Feature reduction, as the preprocessing step, is one of the most important steps in data mining process (Tsai & Hsiao, 2010) and is the first most important step in developing an SVM forecaster (Cao et al., 2006). In the model all available variables can be used as inputs of SVM, but irrelevant features or correlated features could deteriorate the generalization performance of SVM. There are many methods of feature reduction, among them: stepwise regression, factor analysis, genetic algorithms, decision trees and autoencoding. For the current study the feature reduction method of PCA was chosen. PCA has demonstrated the ability to improve the generalization performance of SVM (Cao et al., 2006). In models using financial information, for example bankruptcy predictions, applying PCA increased the performance of prediction (Tsai, 2009).

PCA is a multivariate statistical technique. It aims at reducing the dimensionality of a database with a large number of interrelated variables. In particular, it extracts a small set of factors or components that are constituted of highly correlated elements, while retaining their original characters. After performing PCA, the uncorrelated variables which are called components, will replace the original variables. The total variability of a dataset produced by the complete set of m variables can often be accounted for primarily by a smaller set of k components of these variables (kbm). Therefore, the new dataset consists of n records on k components rather than n records on m variables as the original one. Specifically, eigenvalues and eigenvectors of the principal components are computed in order to find a linear combination of the original variables that counts for the greatest variance. The first principal component accounts for as much of the variability in the data and the second principal component accounts for the remaining variability and so on. Particularly, the level of the variability for each feature lies in the range [0, 1], in which the feature with 1 represents the highest variability. Therefore, if we need the components (i.e. features) which can explain 90% (i.e. 0.9) of the variability, features with 90% of the variability or higher can be selected (Jolliffe, 2002).

In the current study the variables (vectors) are the 58 financial ratios of all the companies remaining in the database for all quarters. Each variable is examined based on its ability to provide information regarding the total variability of the dataset. The first Principal Component (PC) provides the most information, the next PC is analyzed using the remaining variables and provides a lower level of variability, the remaining variables provide decreasing information levels. The eigenvalues represent a measure of the variance explained by the principal component. It is common practice to use the Kaiser criterion, discard all variables with an eigenvalue smaller than 1 (Costello & Osborne, 2005).

Each principal component is a linear combination of the complete dataset; however each variable in the original set has a different coefficient which rates its weight in calculating the principal component, variables with a coefficient lower than 0.3 were discarded. These discarded variables are used in the computerized analysis; however they are eliminated in examination of the principal components.

The remaining principal components are the explanatory variables. Table 3 presents those principal components that were common for all of the five datasets (provided in the imputation stage), for each industry.

Table 3: Principal Componentsa
Ratio Classificationb	Accounting descriptorc	# Industries the PCA appearsd	Mining	Construction	Manufacturing	Transportation, Communication, Electric, Gas and Sanitary Services	Wholesale Trade	Retail Trade	Finance, Insurance and Real Estate
Ability to pay current liabilities	ΔQuick Ratio	6	X	X	X	X			X
	ΔWorking capital	5	X		X	X		X	X
	Current Ratio	5	X		X	X	X
	Quick Ratio	4	X		X	X
	Sales to total working capital	4	X			X	X
	ΔWorking capital to total assets	4	X		X	X
	Working capital to total assets	1					X
Cash conversion cycle	Days sales in Accounting Recv.	6	X	X		X	X	X	X
	Δinventory	6	X	X	X	X			X
	ΔInventory Turnover	6	X	X	X	X			X
	Sales to total Inventory	5	X	X		X			X
	Inventory Turnover	4			X		X	X
	ΔSales to total Inventory	4	X			X		X
	Inventory to total assets	3			X		X
	ΔDays sales in Accounting Recv.	3		X		X			X
	Account Receivable Turnover	1						X
	ΔInventory to total assets	1					X
Ability to pay long-term debt	ΔEquity/Fixed assets	7		X	X	X	X	X	X
	ΔOne period lag in Capital Expenditures/total assets	7	X	X	X	X	X		X
	Equity/Fixed assets	6	X	X	X	X			X
	Total Debt To Equity	5			X	X	X	X
	Times Interest Earned	5	X	X	X				X
	ΔTimes Interest Earned	5	X	X		X	X		X
	Long-Term Debt/Equity	4	X			X		X
	ΔTotal Long-Term Debt	4	X	X		X	X
	ΔCapital Expenditures/total assets	2					X	X
	Cash From Operations to Total Debt	1				X
Profitability	ΔGross Profit Margin	7	X	X	X	X	X		X
	Sales to Fixed assets	6	X		X	X	X	X
	ΔResearch & Development Expense	6	X	X		X	X	X	X
	ΔOperating Income to Total assets	6	X		X	X	X	X
	ΔNet Profit Margin	5	X		X	X		X
	ROA	4	X				X	X
	Net Income over OCF	4			X	X	X	X
	ΔDepreciation (&Amortization), IS	4	X	X		X		X
	ΔTotal Revenue	4			X	X	X	X
	ΔDepreciation over Plant	4	X	X					X
	ΔSales/Total Assest	4	X	X					X
	ΔEBITDA Margin Ratio	4	X	X					X
	ROE	3	X				X
	Pre taxes income/Sales	3	X	X					X
	EBITDA Margin Ratio	2					X	X
	Gross Profit Margin	1					X
	Net Profit Margin	1					X
	Operating Income to Total assets	1			X
	ΔPre taxes income/Sales	1					X
Shares as investment	Payment Of Dividends as % of operating cash flow	2		X					X
	ΔDividends per share	1					X
Principal variables in each industrye			29	20	21	28	26	18	19
a The ratios identified as principal components using PCA. The analysis was run five times on the five different data sets derived from the imputations  stage. Only variables which were identified as principal components in all five iterations are presented.
b Based on Harrison et al. (2011).
c Δ indicates changes. In calculating % Δ, observations with zero denominators are excluded and absolute values are used in all denominators.
d How many industries does the specific ratio appear as a principal component. Sum of the number of components in the row.
e How many ratios were identified as principal components in each industry.

As can be seen from Table 3, all of the financial ratios represent all major financial areas of analysis (Harrison et al., 2011) with profitability being most prominent (19 financial ratios), then cash conversion cycle and ability to pay long-term debt (each with 10 financial ratios) and ability to pay current liabilities (with 7 financial ratios) and analysis of shares as an investment with 2 financial ratios.

In total 48 financial ratios (out of the original 58) were found to be explanatory variables for all industries, for each industry between 18 and 29 financial ratios were used to create the model, on average 23.4 explanatory variables for each industry. The PCA was able to reduce the number of variables, to be used in the model, for each industry from 58 variables to an average of 23.4, a reduction of approximately 60%.

Data training

The purpose of data training is to label the variables to be implemented in the model, in this case to label the dependent and independent variables. The independent variables are the financial ratios for year Xi the dependent variable is the change (+/-) in earnings for the year Xi+1, above the drift. The drift term was estimated as the mean earnings per share change over the four prior quarters to the estimated quarter (Ou & Penman, 1989).

Testing data

Once the model is created, using the data training set, it is used to examine its accuracy on the testing data set. . The independent variable of the testing data is the change in earnings between Q2/2017 and Q3/2017.

Model construction

The purpose of the research is to construct a model which will predict the change in earnings one period ahead, after removal of the earnings drift. The model will present the change in earnings in the form increase (+) or decrease (-).

There are many statistical techniques that may be used to create the model. SVM is a popular tool in time series forecasting, due to its generalization performance ability, the absence of local minima and the sparse representation of solution (Cao et al., 2006). Unlike most of the traditional methods which implement the Empirical Risk Minimization Principal, SVM seeks to minimize an upper bound of the generalization error rather than minimize the training error (Vapnik, 2013). It is a supervised machine learning algorithm which is mostly used in classification problems. In this algorithm, each data item is plotted as a point in n-dimensional space (where n is number of features) with the value of each feature being the value of a particular coordinate. Then, a classification is performed by finding the hyper-plane that differentiates the two classes very well. Support Vectors are simply the co-ordinates of individual observation.

Kernel methods are a class of algorithms for pattern analysis. The linear function and the radial basis function (RBF) are the two popular kernel functions suggested for SVM classifiers. As opposed to the linear kernel, the RBF kernel nonlinearly maps the samples into the high-dimensional space, which makes it feasible for nonlinear problems. One of the challenging problems using RBF kernel to build SVM model is the selection of parameter values for (C, σ) in order to ensure satisfactory prediction performance. The RBF model may yield poor performance if these parameters are not carefully chosen (Li et al., 2015).

The current research implements the SVM model in R version 3.4.1 using library e1071 with RBF kernel. A five cross validation was used to choose the best (C, σ), for each model, that resulted in the best prediction of the training data set.

Results and Discussion

The analysis creates 5 models for the 5 data sets (from the 5 different versions of imputation). Each model predicts for each company whether there will be an increase in profitability in the next quarter or a decrease. The prediction is than compared to the actual performance of the company in Q3/2017. For each company if 4 or more of the data sets have the same prediction that is the prediction that is chosen. Those companies where only 3, or less, of the datasets have the same predictions are ignored in the accuracy test (Ou & Penman, 1989, used a probability of<40% and>60% to eliminate uncertain predictions).

The results of the model are presented in Table 4.

Table 4: Model Accuracy Resultsa
	Average	Mining	Construction	Manufacturing	Transportation, Communications, Electric, Gas and Sanitary Services	Wholesale Trade	Retail Trade	Finance, Insurance and Real Estate	Services
PCA and SVM	63.4%	80.2%	84.2%	58.3%	57.2%	49.1%	63.1%	56.8%	57.9%
Stepwise Multivariate Logistic Regression	68.1%	71.6%	71.0%	63.4%	68.2%	69.0%	67.2%	68.2%	66.4%
a The percentage of companies for which the model was able to predict the actual change in earnings between the Q2/2017 to Q3/2017.

As can be seen from Table 4 the models were able to provide an accuracy of prediction between 49.1% (wholesale trade industry) and 84.2% (construction industry) with an average of 63.4%. These results represent a very high variance between the different industries; analysis of the data did not provide an explanation for this variation. No correlation was found between the number of companies, the number of variables or the number of observation and the accuracy level of the industry. The number of the principal components found in the PCA did not explain the level of accuracy of the model’s prediction in the different industries.

In order to evaluate the SVM model the same data was then used to model earnings prediction using stepwise multivariate logistic regression. Stepwise multivariate logistic regression is the traditional analysis used in many previous studies (Ou & Penman, 1989; Holthausen & Larcker, 1992; Bird et al., 2001; Bernard et al., 1997; Setiono and Strong, 1998). The results of the stepwise multivariate regression are also presented in Table 4. While the average accuracy for all industries is higher 68.1% it should be noted that when examining the specific industries the highest accuracy rate is only 71.6% as compared to the 84.2% of the SVM model.

No apparent connection, such as industry size, data completeness (as presented by removal of outliers and imputation) or industry characteristics, was found to explain why the models were able to predict some industries better than others.

Conclusion

The focus of this study has been to implement machine learning techniques, specifically SVM, on XBRL data and create a model to predict earnings movement. Such a model will allow continuous analysis of large amounts of data, as it becomes available and would be incremental for investment decision making.

The findings of the study suggest that machine learning can be used to predict the change in one quarter ahead earnings, based on XBRL data. The results of the model, which had an accuracy rate of up to 84.2%, depending on the industry, are compatible with previous research, which was based on traditional statistical methods (multiple regressions) models. A comparison of the results of the SVM model with stepwise multivariate logistic regression shows that although the average accuracy for all industries is lower using SVM (63.4% compared to 68.1%), the ability of the model to accurately predict specific industries is much higher (84.2% to 71.6%).

The current model, based on SVM and XBRL data has several advantages over the traditional statistical models based on COMPUSTAT:

1. XBRL data provides more timely information and therefore may be used immediately for decision making.

2. XBRL allows updating the model every quarter as information is published.

3. Machine learning provides an advanced statistical tool which may be used to analyze large amounts of data as they become available.

4. SVM has been shown to be a more effective tool when non-linear data, such as financial information, is used.

The study contributes to previous research by introducing a detailed machine learning model used in conjunction with a comprehensive range of accounting data extracted from XBRL company filings. The study aims to close part of the gap in the literature regarding earnings movement prediction using machine learning techniques.

However, even though the model presented has many advantages it does not provide a definitive answer as to the superiority of SVM, the model classified some industries more accurately and some less accurately then the traditional method of stepwise multivariate logistic regression. These inconclusive results may be attributed to the relative short time period of the available data (from 2012), SEC mandated XBRL. Advanced machine learning techniques, unlike traditional statistical methods, improve with large amounts of data, the short time period limits the amount of data available, suggesting that SVM results will improve in the future.

Another explanation for the inconclusive results may be the models used, the study only examines the combination of PCA-SVM and possible extensions of this study should be examining other machine learning techniques for both feature reduction and model construction.
While the results of the study are inconclusive as to the superiority of the SVM model presented, it does provide a detailed viable model for predicting earnings movement utilizing machine learning and comprehensive XBRL data.

Appendix 1: Variables
1	Account Receivable Turnover
2	Current Ratio
3	Quick Ratio
4	Inventory Turnover
5	Total Debt To Equity
6	ROA
7	ROE
8	Gross Profit Margin
9	Days sales in Accounting Recv.
10	Inventory to total assets
11	Depreciation over Plant
12	Long-Term Debt/Equity
13	Equity/Fixed assets
14	Times Interest Earned
15	Sales/Total Assest
16	Pre taxes income/Sales
17	Net Profit Margin
18	Sales to total cash
19	Sales to total Inventory
20	Sales to total working capital
21	Sales to Fixed assets
22	Working capital to total assets
23	Operating Income to Total assets
24	EBITDA Margin Ratio
25	Cash From Operations (CFO) to Total Debt
26	Payment Of Dividends as % of OCF
27	Net Income over OCF
28	ΔDepreciation (&Amortization), IS
29	Δinventory
30	ΔResearch & Development Expense
31	ΔTotal Assets
32	ΔTotal Long-Term Debt
33	ΔTotal Revenue
34	ΔCurrent Ratio
35	ΔQuick Ratio
36	ΔInventory Turnover
37	ΔDividends per share
38	ΔTotal Debt To Equity
39	ΔROE
40	ΔGross Profit Margin
41	ΔWorking capital
42	ΔDays sales in Accounting Recv.
43	ΔInventory to total assets
44	ΔDepreciation over Plant
45	ΔCapital Expenditures/total assets
46	ΔLong-Term Debt/Equity
47	ΔEquity/Fixed assets
48	ΔTimes Interest Earned
49	ΔSales/Total Assest
50	ΔPre taxes income/Sales
51	ΔNet Profit Margin
52	ΔSales to total Inventory
53	ΔSales to total working capital
54	ΔResearch & Development Expense to Sales
55	ΔWorking capital to total assets
56	ΔOperating Income to Total assets
57	ΔEBITDA Margin Ratio
58	ΔOne period lag Capital Expenditures/total assets

References

1. Abarbanell, J., &amli; Bushee, B.J. (1997). Fundamental analysis, future EliS, and stock lirices. Journal of Accounting Research, 35(1), 1-24.
2. Alam, li., &amli; Brown, C.A. (2006). Disaggregated earnings and the lirediction of ROE and stock lirices: A case of the banking industry. Review of Accounting and Finance, 5(4), 443–463.
3. Amani, F.A., &amli; Fadlalla, A.M. (2017). Data mining alililications in accounting: A review of the literature and organizing framework. International Journal of Accounting Information Systems, 24(1), 32-58.
4. Ball, R., &amli; Brown, li. (1968). An emliirical evaluation of accounting income numbers. Journal of Accounting Research, 6(2), 159–178.
5. Ball, R., &amli; Shivakumar, L. (2008). How much new information is there in earningsΔ Journal of Accounting Research, 46(5), 975-1016.
6. Barak, S., &amli; Modarres, M. (2015). Develoliing an aliliroach to evaluate stocks by forecasting effective features with data mining methods. Exliert Systems with Alililications, 42(3), 1325-1339.
7. Baranes, A., &amli; lialas, R. (2017). The lirediction of earnings movements using accounting data: Using XBRL. International Journal of Accounting Research, 4(2), 1–7.
8. Barbato, G., Barini, E.M., Genta, G., &amli; Levi, R. (2011). Features and lierformance of some outlier detection methods. Journal of Alililied Statistics, 38(10), 2133–2149.
9. Beaver, W.H. (1968). The information content of annual earnings announcements. Journal of Accounting Research, 6(1–2), 67-92.
10. Bernard, V., Thomas, J., &amli; Wahlen, J. (1997). Accounting-based stock lirice anomalies: Seliarating market inefficiencies from risk. Contemliorary Accounting Research, 14(2), 89–136.
11. Bernard, V.L., &amli; Thomas, J.K. (1990). Evidence that stock lirices do not fully reflect the imlilications of current earnings for future earnings. Journal of Accounting and Economics, 13(4), 305–340.
12. Bird, R., Gerlach, R., &amli; Hall, A.D. (2001). The lirediction of earnings movements using accounting data: An ulidate and extension of ou and lienman. Journal of Asset Management, 2(2), 180–195.
13. Bloomfield, R.J., Libby, R., &amli; Nelson, M.W. (2003). Do investors overrely on old elements of the earnings time seriesΔ Contemliorary Accounting Research, 20(1), 1–31.
14. Boritz, J.E., &amli; No, W.G. (2008). SEC’s XBRL voluntary filing lirogram on EDGAR: A case for quality assurance. Current, 2(2), A36–A50.
15. Boritz, J.E., &amli; No, W.G. (2013). The Quality of Interactive Data: XBRL versus Comliustat, Yahoo Finance, and Google Finance. Working lialier.
16. Cao, L.J., Jingqing, Z., Zongwu, C., &amli; Guan, L.K. (2006). An emliirical study of dimensionality reduction in suliliort vector machine. Neural Network World, 16(3), 177-192.
17. Chandwani, D., &amli; Saluja, M.S. (2014). Stock direction forecasting techniques : An emliirical study combining machine learning system with market indicators in the indian context. International Journal of Comliuter Alililications, 92(11), 8-17.
18. Chang, C., Mcaleer, M., &amli; Wong, W.K. (2017). Research ideas for the journal of management. Journal of Management Information and Decision Sciences, 20(2), 1–5.
19. Chychyla, R., &amli; Kogan, A. (2015). Using XBRL to conduct a large-scale study of discreliancies between the accounting numbers in comliustat and SEC 10-K Filings. Journal of Information Systems, 29(1), 37–72.
20. Costello, A.B., &amli; Osborne, J.W. (2005). Best liractices in exliloratory factor analysis : Four recommendations for getting the most from your analysis. liractical Assessment, Research &amli; Education, 10(2), 1-9.
21. D’Souza, J.M., Ramesh, K., &amli; Shen, M. (2010). The interdeliendence between institutional ownershili and information dissemination by data aggregators. Accounting Review.
22. Danėnas, li. (2013). Suliliort vector machines based classifiers in intelligent decision suliliort system for credit risk evaluation. Vilnius University, Lithuania, 8(3), 46-58.
23. Danenas, li., &amli; Garsva, G. (2011). SVM and XBRL based decision ssuliliort system for credit risk evaluation. 17th International Conference on Information and Software Technologies (IT 2011), Technologija, Kaunas, Lithuania (January 2011), 190–198.
24. Debreceny, R., Farewell, S., liiechocki, M., Felden, C., &amli; Gräning, A. (2010). Does it add uliΔ Early evidence on the data quality of XBRL filings to the SEC. Journal of Accounting and liublic liolicy, 29(3), 296–306.
25. Debreceny, R.S., Farewell, S.M., liiechocki, M., Felden, C., Gräning, A., &amli; D’Eri, A. (2011). Flex or freakΔ Extensions in XBRL disclosures to the SEC. Accounting Horizons, 25(4), 631–657.
26. Du, H., Vasarhelyi, M.A, &amli; Zheng, X. (2011). XBRL Mandate: Thousands of Filing Errors and So WhatΔ Working lialier: httli://eycarat.faculty.ku.edu//myssi/_lidf/3-Du et.
27. Elliott, R.K. (1992). The third wave breaks on the shores of accounting. Accounting Horizons, 6(2), 61–85.
28. Etemadi, H., Ahmadliour, A., &amli; Moshashaei, S.M. (2015). Earnings lier share forecast using extracted rules from trained neural network by genetic algorithm. Comliutational Economics, 46(1), 55–63.
29. Finger, C.A. (1994). The ability of earnings to liredict future earnigns and cash flow. The Journal of Accounting Research, 32(2), 210–223.
30. Foster, G., Olsen, C., &amli; Shevlin, T. (1984). Earnings releases, anomalies, and the behavior of security returns. The Accounting Review, 59(4), 574–603.
31. Han, S., &amli; Chen, R.C. (2007). Using SVM with financial statement analysis for lirediction of stocks. communications of the IIMA, 7(4), 63–72.
32. Harrison, W.T., Horngern, C.T., Thomas, W.C., &amli; Suwardy, T. (2011). Financial Accounting-International Financial Reliorting Standards (Eighth Edition). Singaliore: liearson Education South Asia.
33. Henselmann, K., Ditter, D., &amli; Scherr, E. (2015). Irregularities in accounting numbers and earnings management—a novel aliliroach based on SEC XBRL Filings. Journal of Emerging Technologies in Accounting, 12(1), 117–151.
34. Holthausen, R.W., &amli; Larcker, D.F. (1992). The lirediction of stock returns using financial statement information. Journal of Accounting and Economics, 15(2), 373–411.
35. Huang, C.F. (2012). A hybrid stock selection model using genetic algorithms and suliliort vector regression. Alililied Soft Comliuting, 12(2), 807–818.
36. Jolliffe, I.T. (2002). lirincilial Comlionent Analysis (Second Editio). New York: Sliringer.
37. Kamley, S., Jaloree, S., &amli; Thakur, R.S. (2016). lierformance forecasting of share market using machine learning techniques: A Review. International Journal of Electrical and Comliuter Engineering, 6(6), 3196–3204.
38. Kaya, D., &amli; lironobis, li. (2016). The benefits of structured data across the information sulilily chain: Initial evidence on XBRL adolition and loan contracting of lirivate firms. Journal of Accounting and liublic liolicy, 35(4), 417–436.
39. Kinney, M.R., &amli; Swanson, E.li. (1993). The accuracy and adequacy of tax data in COMliUSTAT. Journal of the American Taxation Association, 15(1), 121-132.
40. Konchitchki, Y., &amli; liatatoukas, li.N. (2014). Taking the liulse of the real economy using financial statement analysis: Imlilications for macro forecasting and stock valuation. Accounting Review, 89(2), 669–694.
41. Lev, B., &amli; Gu, F. (2016). The end of accounting and the liath forward for investors and managers (First Edition). John Wiley &amli; Sons.
42. Li, C.K., Liang, D., Lin, F., &amli; Chen, K.L. (2015). The alililication of corliorate governance indicators with XBRL technology to financial crisis lirediction. Emerging Markets Finance and Trade, 51(1), 58–72.
43. Lin, F., Liang, D., &amli; Chiu, S.J. (2008). The study of a financial crisis lirediction model based on XBRL. Ninth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and liarallel/Distributed Comliuting.
44. Liu, C., &amli; O’Farrell, G. (2013). The role of accounting values in the relation between XBRL and forecast accuracy. International Journal of Accounting and Information Management, 21(4), 297–313.
45. Miguel, J.G.S. (1977). The reliability of R&amli;D data in COMliUSTAT and 10-K Reliorts. The Accounting Review, 52(3), 638–641.
46. Ou, J.A. (1990). The information content of nonearnings accounting numbers as earnings liredictors. Journal of Accounting Research, 28(1), 144–163.
47. Ou, J.A., &amli; lienman, S.H. (1989). Financial statement analysis and the lirediction of stock returns. Journal of Accounting and Economics, 11(4), 295–329.
48. lienman, S.H., &amli; Zhang, X.J. (2002). Accounting conservatism, the auality of earnings, and stock returns. Accounting Review, 77(2), 237–264.
49. Qiu, X.Y., Srinivasaan, li. &amli; Hu, Y. (2014). Suliervised learning models to liredict firm lierformance with annual reliorts: an emliirical study. Journal of the Association for Information Science and Technology, 65(2), 400–413.
50. Rajakumar, M.li., &amli; Ramya, J. (2017). A comliarison of intelligent soft comliuting techniques for forecasting earnings lier share. International Journal of liure and Alililied Mathematics, 114(9), 167–177.
51. Ralioso, R.D.C.T., &amli; Cruz, A.J.D.O. (2002). Stock market lirediction based on fundamentalist analysis with fuzzy- neural networks 2 inliut data and sector choice 3 the choice of economic indicators. In liroc. of the 3rd WSEAS Int. Conf. on Neural Networks and Alililications (NNA’02).
52. Rosenberg, B., &amli; Houglet, M. (1974). Error rates in CRSli and COMliUSTAT data bases and their imlilications. The Journal of Finance, 29(4), 1303–1310.
53. Roychowdhury, S., &amli; Sletten, E. (2012). Voluntary disclosure incentives and earnings informativeness. Accounting Review, 87(5), 1679–1708.
54. Rubin, D.B. (1996). Multilile imliutation after 18+ years. Journal of the American Statistical Association, 91(434), 473-489.
55. Sali, M., &amli; Awan, A.M. (2005). Stock market lirediction using suliliort vector machines. Jurnal Teknologi Maklumat 17(2), 27–35.
56. Setiono, B., &amli; Strong, N. (1998a). liredicting stock returns using financial statement information. Journal of Business Finance and Accounting, 25(6), 631–657.
57. Setiono, B., &amli; Strong, N. (1998b). liredicting stock returns using financial statement information. Journal of Business Finance and Accounting, 25(6), 631–657.
58. Shroff, li.K. (1999). The variability of earnings and non-earnings information and earnings lirediction. Journal of Business Finance and Accounting, 26(8), 863–882.
59. Stober, T.L. (1992). Summary financial statement measures and analysts’ forecasts of earnings. Journal of Accounting and Economics, 15(3), 347–372.
60. Tallalially, li., Luehlfing, M.S., &amli; Motha, M. (2011). The liartnershili of EDGAR online And XBRL-should comliustat careΔ The Review of Business Information Systems, 15(3), 39–46.
61. Tsai, C.F. (2009). Feature selection in bankrulitcy lirediction. Knowledge-Based Systems, 22(2), 120–127.
62. Tsai, C.F., &amli; Hsiao, Y.C. (2010). Combining multilile feature selection methods for stock lirediction: Union, intersection, and multi-intersection aliliroaches. Decision Suliliort Systems, 50(1), 258–269.
63. Valinik, V. (2013). The nature of statistical learning theory. Sliringer Science &amli; Business Media, 7(7), 945-954.
64. Vasarhelyi, M.A., Kogan, A., &amli; Tuttle, B.M. (2015). Big data in accounting: An overview. Accounting Horizons, 29(2), 381–396.
65. Visvanathan, G. (2006). An emliirical investigation of “closeness to cash” as a determinant of earnings reslionse coefficients. Accounting and Business Research, 36(2), 109–120.
66. Williams, K.L. (2015). The lirediction of future earnings using financial statement information: Are XBRL comliany filings uli to the taskΔ lihD Thesis: The University of Mississililii.
67. Wu, W., &amli; Xu, J. (2006). Fundamental analysis of stock lirice by artificial neural networks model based on rough set theory. World Journal of Modeling an Simulation, 2(1), 36–44.
68. Yang, D.C., Vasarhelyi, M.A., &amli; Liu, C. (2003). A note on the using of accounting databases. Industrial Management &amli; Data Systems, 103(3), 204–210.