Keywords

Decision Environments; States of Nature; Decision Alternatives; Uncertainty; Risk; Certainty.

Introduction

Every day human’s feasible economic activities are based on generating alternatives and accessing them. Decisions may be made under social pressure or time constraints that interfere with a careful consideration of the options and consequences. Decisions may be influenced by one's emotional state at the time a decision is made (Taghavifard et al., 2009). Operations research encompasses a wide range of problem-solving techniques and methods applied in the pursuit of improved decision making. There are lots of techniques that assist decision-makers in selecting the best alternative from the set of feasible alternatives. Many researchers analyzed the importance of a rational decision making in a constantly changing and risky environment for real-world problems.

This paper aim is to illustrate and explain the decision analysis process under different decision criteria, type, and quality of available information. We intend to describe the basic elements in the analysis of decision alternatives and choices. Decision making under risky and uncertain situations has a theorical and practical importance, that’s the reason we’ll review several techniques in this paper. We intend to use a case study, as an example for appropriate expression of these techniques. We are aware that most of the time people are more likely to rely on personal experience than on information about probabilities. The fundamental concerns of decision making are combining information about probability with information about desires and interests (Taghavifard et al., 2009).

Decision Environments

Decision making is identifying and choosing alternatives based on the values and preferences of the decision maker. Making a decision implies that there are alternative choices to be considered, and in such a case we want not only to identify as many of these alternatives as possible but to choose the one that best fits with our goals, objectives, desires, values, and so on (Harris, 1980).

The decision maker is unsure of what situation will occur in the future and moreover, he has no control over what will happen at the time the decision is made. The decision-making environment is often characterized by three states: certainty, uncertainty, risk, conflict.

Certainty

A decision made in safe conditions, certainty, is a condition for which you know which state of nature will occur in the future. We can think of security as a single case or an alternative. In conditions of complete security, only one condition or a variation of conditions is possible which have no effect on the consequences of a certain alternative. So, the decision is not influenced by uncontrolled factors. The assumption that complete certainty exists, when the information is not known with complete certainty, makes finding an optimal and approximate solution quite reasonable. Certainty is a theoretical and rarely a practical possibility. Very few well-structured and well-programmed decisions and very few decision-makers can be totally sure of the consequences that will really happen. However, a decision maker can choose a model as if it occurred in safe conditions only if he believes that his modeling with probabilities would not add anything new to the problem analysis. When it is known for certain which of the possible future conditions will actually happen, the decision is usually relatively straight forward (Stevenson, 2012).

Uncertainty

In very few decision-making situations is perfect information - all the needed facts - available. Most decisions are made in the face of uncertainty (Leake, 1998; Belton & Stewart, 2002). In decision making under pure uncertainty, the decision maker has absolutely no knowledge, not even about the likelihood of occurrence for any state of nature. In such situations, the decision maker's behavior is purely based on his/her attitude toward the unknown (Eiser & van der Pligt, 2015). Some of these behaviors are optimistic and some pessimistic ore something between.

Uncertainty means that it is impossible to assess the likelihood of various possible future events (Stevenson, 2012). A decision made in conditions of uncertainty has more than one state of nature but the decision maker cannot determine the probabilities of the occurrence of each state. In conditions of complete uncertainty not only the consequences of the decision can be predicted but we will have very little confidence in any possible situation or in the possibility of their occurrence. Also, the decision structure will be poor and the information will be limited or doubtful. Conditions of complete uncertainty are also very rare. In practice, complete security/uncertainty extremes are unlikely to occur.

Risk

Whenever the decision maker has some knowledge regarding the states of nature, he/she may be able to assign subjective probability estimates for the occurrence of each state. In such cases, the problem is classified as decision making under risk (Rowe, 1988). Probability enters into the process by playing the role of a substitute for certainty - a substitute for complete knowledge (Leake, 1998). Risk means that certain parameters have probabilistic outcomes (Stevenson, 2012). A decision made under risky conditions has more than one state of nature. We can make assumptions that the decision maker can arrive at a probability estimate for the occurrence of each of these states of nature. Managers usually make some kind of assessment regarding the possible consequences even when the decision situations are very unclear. When security conditions are not present but we are able to make reliable predictions using certain probabilities, we can say that decision-making is done under risk conditions and probability theory takes special importance.

Conflict

A decision taken in a conflict situation exists when the interests of two or more decision makers are in conflict and they are in competition with each other. In other words, if decision maker A benefits from following a certain course of action, this happens if decision maker B has taken a fully defined course of action. So, decision makers are interested not only in their own actions but also in the actions of others when making decisions in conflict situations. These situations are part of the game theory.

Decision theory is mainly related to decision making in conditions of risk and uncertainty. If we imagine a scale to represent the measure of uncertainty of a decision, it would have two edges where one would indicate certainty conditions while the other would indicate complete uncertainty conditions. The risk would take an intermediate place (Figure 1).

Components and Criteria Used In Decision Making

A decision-making situation has several components:

• The actual decisions
• The current events that may occur in the future, known as the state of nature.

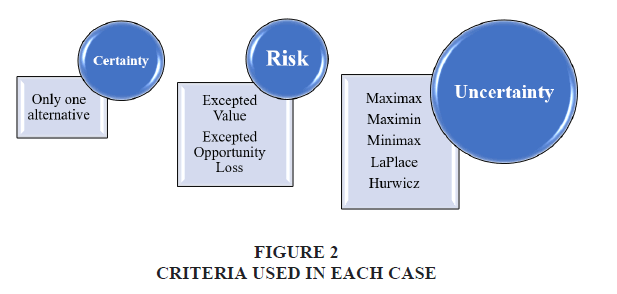
In order to facilitate the analysis of different decision situations and with the intention of making the best decision we can organize the data in a payoff table. A payoff table shows the expected payoffs for each alternative under the various possible states of nature (Stevenson, 2012). In general, a payoff table is a tool that serves to organize and illustrate the results for different decisions having given different states of nature for a decision-making problem. It is often possible to assign probabilities to different states of nature that assist the decision maker in choosing the decision that yields the best outcome. However, in some cases, the decision maker is not able to determine the probabilities (Figure 2).

We can use several criteria’s in each case:

• Certainty - a single case or an alternative, no need to use a criterion.
• Uncertainty - Several criteria such as: Maximax, Maximin, Minmax regret, Laplace, Hurwicz.
• Risk - Several criteria such as: Expected Values, Expected Opportunity Loss.

It is a challenging task to compare several courses of action and then select one action to be implemented. Difficulties in decision making arise through complexities in decision alternatives. In addition, unknown factors always intrude upon the problem situation, and seldom are outcomes known with certainty. Almost always, an outcome depends upon the reactions of other people who may be undecided themselves. It is no wonder that decision-makers sometimes postpone choices for as long as possible. Then, when they finally decide, they neglect to consider all the implications of their decision (Wickham, 1998).

Business decision making is almost always accompanied by conditions of uncertainty. To illustrate the different decision-making criteria, we will use a case study, which tries to make a connection with the current situation around the world, Covid-19. We have taken a case study about a night club which due to the pandemic conditions is faced with several decisions’ alternatives. Alike this night club many others around the world are in the same situation of uncertainty. This uncertainty means that it is the case of decision making without probabilities. The following table illustrates the construction of the table of results. The night club has to decide what to do and it faces several decision alternatives:

• Maintain the current status quo and wait for the situation to improve (cost of staying without work approximately €20,000 for 6 months).
• Close the activity and sell it (Price of selling €60,000)
• Change the type of business investing in some furniture (Cost =€10,000) and change from e night club to a simple restaurant.
• Change the type of business investing a minimal amount (Cost = €5,000) and change from a night club to a stand up and karaoke bar that can operate within the pandemic restrictions.

The investor will choose between these four alternatives. Future states of nature that will determine how much profit the investor will provide are Pandemic ends this spring and Pandemic doesn’t end this spring. The gains/losses that will result from each decision for each state of nature are shown in Table 1.

Table 1 Alternatives, States Of Nature And Results
Alternative	States of nature
	Pandemic ends	Pandemic doesn’t end
Maintain the current status quo	€100,000	-€20,000
Close the activity	€60,000	€60,000
Change the type of business 1	€70,000	-€30,000
Change the type of business 2	€80,000	€40,000

Decision Making Without probabilities

Decision making under pure uncertainty, the decision maker has no knowledge regarding any of the states of nature outcomes, and/or it is costly to obtain the needed information. In such cases, the decision making depends merely on the decision maker's personality type (Biswas, 1997; Samin et al., 2022). Several criteria are available to make the actual decision making without probabilities. These decision criteria include the maximax criterion, the maximin criterion, minimax or regret criterion, Hurwicz, and LaPlace or likelihood criterion. The decision maker must choose the criterion or combination of criteria that will best suit his needs. In our case the decision maker is in conditions of uncertainty and depending on his personal predispositions or feelings, we expect he will behave as optimistic, pessimistic or something in between. Let's start applying the criteria for this case.

With the maximum criterion, the decision maker chooses the decision that would result in the maximum of maximum results. (In fact, this is exactly the reason for the name - a maximum of maximums.) The maximum criterion is based on the assumption that the decision maker is optimistic. The decision maker assumes that the most favorable state of nature will occur for each decision alternative. The maximax approach is an optimistic, “go for it” strategy, it does not take into account any payoff other than the best (Stevenson, 2012).

The application of the maximax criterion for our case is shown in Table 2. The decision maker will first select the maximum payoffs for each decision and next chose the maximum €100,000; thus, the corresponding decision is to maintain the current status quo and wait.

Table 2 Maximax Criterion
Alternative	States of nature
	Pandemic ends	Pandemic doesn’t end	Maximax
Maintain the current status quo	€100,000	-€20,000	€100,000
Close the activity	€60,000	€60,000	€60,000
Change the type of business 1	€70,000	-€30,000	€70,000
Change the type of business 2	€80,000	€40,000	€80,000

Although, the decision to maintain the current status quo results in a profit of €100,000, such a decision completely ignores the possibility of a potential loss of €20,000. The decision maker assumes an optimistic future regarding the states of nature.

In contrast to the maximax criterion, which is very optimistic, the maximin criterion is pessimistic. With the maximin criterion, the decision maker chooses the decision that will reflect the maximum of the minimum results. For each decision alternative, the decision maker assumes that the minimum outcome will occur. Then from these minimum results, the maximum is selected. The actual outcome may not be as bad as that, but this approach establishes a “guaranteed minimum” (Stevenson, 2012).

The application of the maximin criterion for our case is shown in Table 3. The decision maker will first select the minimum payoffs for each decision and next chose the maximum €60,000; thus, the corresponding decision is to close the activity. This decision can be considered relatively conservative, as the alternatives considered include only the worst results that can occur. The decision maker assumes a pessimistic future regarding the states of nature.

Table 3 Maximax Criterion
Alternative	States of nature
	Pandemic ends	Pandemic doesn’t end	Maximin
Maintain the current status quo	€100,000	-€20,000	-€20,000
Close the activity	€60,000	€60,000	€60,000
Change the type of business 1	€70,000	-€30,000	-€30,000
Change the type of business 2	€80,000	€40,000	€40,000

This Minimax regret criterion development is based on the concept of opportunity loss or regret. Regret is the difference between the payoff from the best decision and all other decision payoffs. The minimax regret criterion minimizes the maximum regret (Taylor, 2019). Minimax regret determines the worst regret for each alternative and choose the alternative with the “best worst” (Stevenson 2012). To use the minimax regret criterion, a decision maker must first select the maximum payoff for each state of nature. In our case the maximum payoff for the state of nature “Pandemic ends” is €100,000 and the maximum payoff for the state of nature “Pandemic doesn’t end” is €60,000. Calculate the regrets by subtracting every payoff in each column from the best payoff in that column. The next step is to identify the worst regret for each alternative and the best of these worst regrets would be chosen. The results are summarized in the regret table, Tables 4-6. With this decision criterion, the decision maker tries to avoid losses by choosing the alternative that minimizes the greatest loss.

Table 4 Maximal Payoffs
Alternative	States of nature
	Pandemic ends	Pandemic doesn’t end
Maintain the current status quo	€100,000	-€20,000
Close the activity	€60,000	€60,000
Change the type of business 1	€70,000	-€30,000
Change the type of business 2	€80,000	€40,000

Table 5 Regret Calculation
Alternative	States of nature
	Pandemic ends	Pandemic doesn’t end
Maintain the current status quo	€100,000 - €100,000 = 0	€60,000 + €20,000 = €80,000
Close the activity	€100,000 - €60,000 = €40,000	€60,000 - €60,000 = 0
Change the type of business 1	€100,000 - €70,000 = €30,000	€60,000 + €30,000 = €90,000
Change the type of business 2	€100,000 - €80,000 = €20,000	€60,000 + €40,000 = €20,000

Table 6 Regret Table
Alternative	Regrets
	Pandemic ends	Pandemic doesn’t end	Minimax
Maintain the current status quo	€0	€80,000	€80,000
Close the activity	€40,000	€0	€40,000
Change the type of business 1	€30,000	€90,000	€90,000
Change the type of business 2	€20,000	€20,000	€20,000

According to the minimax criterion, the decision will be to Change the activity to a stand up and karaoke bar. This decision is based on the philosophy that the investor will experience the least amount of regret by changing the type of business 2.

The LaPlace criterion assumes that states of nature are equally likely to occur, i.e. it gives them the same weight. LaPlace criterion determines the average payoff for each alternative and chooses the alternative with the best average. This approach treats the states of nature as equally likely (Stevenson, 2012). The qual likelihood or LaPlace criterion multiplies the decision payoff for each state of nature by an equal weight (Taylor, 2019). Since in our example we have two states of nature we will assign a weight of 0.50 to each one. Next we multiply each payoff for each decision, by these weights (Table 7).

Table 7 Values For Laplace
Alternative	Values
Maintain the current status quo	€100,000 (0.5) - €20,000(0.5) = €40,000
Close the activity	€60,000(0.5) + €60,000(0.5) = €60,000
Change the type of business 1	€70,000(0.5) - €30,000(0.5) = €20,000
Change the type of business 2	€80,000(0.5) + €40,000(0.5) = €60,000

We choose the decision that has the maximum of these weighted values. Since €60,000 is the highest weighted value and we have two decisions that have the same weighted value so the decision is between to Close the activity and Change the type of business 2.

The Hurwicz criterion is a compromise between the maximax and maximin criteria (Taylor, 2029). The principle in which is based this criterion is that the decision maker is neither fully optimistic (as maximax assumes) nor completely pessimistic (as maximin assumes). In fact, decision makers display a mixture of optimism and pessimism. With this criterion, decision payoffs are weighed by an optimism coefficient, which is a measure of decision maker optimism. The coefficient of optimism is α and is a value between zero and one (0 ≤ α ≤ 1). If α=1 then the decision maker will act and think as an optimist; if α=0 then the decision maker is completely pessimistic. Thus, if α is the coefficient of optimism we have that 1 – α, is the coefficient of pessimism. In order to apply this criterion, we have to multiple for each decision alternative, the maximum payoff with α and the minimum payoff with 1-α. For our case if we assume that the manager is more pessimistic then optimistic and α = 0.4. We can calculate the coefficient of pessimism as 1–α=1–0.4=0.6. Table 8 shows the calculations.

Table 8 Hurwicz Criterion
Alternative	Values
Maintain the current status quo	€100,000 (0.4) - €20,000(0.6) = €28,000
Close the activity	€60,000(0.4) + €60,000(0.6) = €60,000
Change the type of business 1	€70,000(0.4) - €30,000(0.6) = €10,000
Change the type of business 2	€80,000(0.4) + €40,000(0.6) = €56,000

 

The Hurwicz criterion selects the decision alternative that corresponds to the maximum weighted value which is €60,000. So, the decision will be to close the activity. The Hurwicz criterion can be considered a completely subjective decision-making criterion.

Decision Making with Probabilities

The decision-making criteria presented so far are based on the assumption that we have no information available on the occurrence or not of a state of nature. Thus, we did not assign probabilities for the occurrence of natural states, except in the case where we assumed that natural events have the same probability of occurrence. The fundamental concerns of decision making are combining information about probability with information about desires and interests (Taghavifard et al., 2009).

It is often possible for the decision maker to have enough knowledge about the future states of nature in order to be able to determine probabilities for their occurrence. Given that probabilities can be assigned several decision criteria can be used. We are going to consider only the criteria of the expected value.

In order to apply the concept of expected value as a decision-making criterion, the decision-maker must first assess the probability of occurrence of each state of nature. Once these assessments have been made the expected value for each decision alternative can be calculated. The expected value is calculated by multiplying each outcome (of a decision) by the probability of its occurrence and then adding these products.

We are aware that the result strongly depends on the probabilities assigned toward each state of nature. Let’s try with different probabilities varying from the more optimistic to the less optimistic. Let us assume that, based on some pandemic forecasts we are able to estimate the probability 0.70 for the state “Pandemic ends” and 0.30 for “Pandemic doesn’t end”. The best decision will be the one with the highest expected value. Since the highest expected value is €68,000, the best decision is to change the type of business to a stand-up and karaoke club (Table 9).

Table 9 Expected Value
Alternative	Values
Maintain the current status quo	€100,000 (0.7) - €20,000(0.3) = €64,000
Close the activity	€60,000(0.7) + €60,000(0.3) = €60,000
Change the type of business 1	€70,000(0.7) - €30,000(0.3) = €40,000
Change the type of business 2	€80,000(0.7) + €40,000(0.3) = €68,000

 

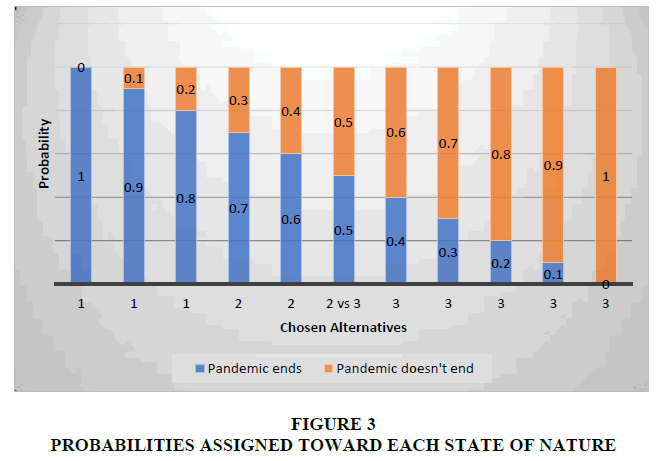
If we change the values of the probabilities assigned toward each state of nature we are going to face different results. The results provided by our calculations are given in the Figure 3 and Table 10.

Table 10 Summarized Results
	Probability
	Optimistic	Pessimistic
	Pandemic ends	Pandemic doesn't end	Chosen alternatives
Maximax	1	0	Maintain the current status quo	1
Expected Value	0.9	0.1	Maintain the current status quo	1
	0.8	0.2	Maintain the current status quo	1
	0.7	0.3	Change the type of business 2	2
	0.6	0.4	Change the type of business 2	2
same as LaPlace	0.5	0.5	Close the activity vs Change the type of activity 2	2 vs 3
	0.4	0.6	Close the activity	3
	0.3	0.7	Close the activity	3
	0.2	0.8	Close the activity	3
	0.1	0.9	Close the activity	3
Maxmin	0	1	Close the activity	3
Minmax			Change the type of business 2

As we can clearly see from the graph if we are totally optimistic that the pandemic ends the best alternative is to maintain the current status quo. This varies from the level of optimism, thus if we decrease the probability of optimism gradually toward pessimism the best alternative changes toward that of closing the activity.

Conclusion

Decisions may rely on personal experience, may be made under social pressure, time constraints may be influenced by one's emotional state, etc., everything could interfere with careful consideration of all the options and consequences. This paper’s aim was to illustrate and explain the decision analysis process under different decision criteria, type, and quality of available information. We described the basic elements in the analysis of decision alternatives and choices. A decision under risky and uncertain situations has theoretical and practical importance, that’s the reason we reviewed several techniques in this paper. We used a case study, as an example for the appropriate expression of these techniques. The concept of uncertainty is so common in our everyday life and we face it constantly and we are aware that most of the time people are more likely to rely on personal experience than on information about probabilities. This paper, is just a first step toward the decision theory and strongly believe that it will serve as a basis for future studies in this interesting field.

References

Belton, V., & Stewart, T. (2002).Multiple criteria decision analysis: an integrated approach. Springer Science & Business Media.

Indexed at, Google Scholar, Crossref

Biswas, T. (1997).Decision-making under uncertainty. Macmillan International Higher Education. Springer.

Google Scholar, Crossref

Eiser, J. R., & van der Pligt, J. (2015).Attitudes and decisions. Psychology Press.

Indexed at, Google Scholar, Crossref

Harris, R. (1998). Introduction to Decision Making. Virtual Salt.

Leake, C.R. (1998). Decision Analysis: An Integrated Approach.Journal of the Operational Research Society, 49, 181-182.

Indexed at, Google Scholar, Crossref

Rowe, W.D. (1988). An Anatomy of Risk. R.E. Krieger Publishing Company.

Google Scholar

Samin, H., Bencomo, N., & Sawyer, P. (2022). Decision-making under uncertainty: be aware of your priorities.Software and Systems Modeling, 1-30.

Indexed at, Google Scholar, Crossref

Stevenson, W.J. (2012).Operations management. New York: McGraw-Hill/Irwin.

Google Scholar

Taghavifard, M.T., Damghani, K.K., & Moghaddam, R.T. (2009). Decision making under uncertain and risky situations. InEnterprise Risk Management Symposium Monograph Society of Actuaries.

Indexed at, Google Scholar

Taylor, B.W. (2019). Introduction to Management Science, 13th Edition. Pearson NY.

Wickham, P. (1998). Strategic Entrepreneurship: A Decision-making Approach to New Venture Creation and Management. London: Pitman.

Received: 12-May-2022, Manuscript No. JMIDS-22-11989; Editor assigned: 16-May-2022, PreQC No. JMIDS-22-11989(PQ); Reviewed: 26-May-2022, QC No. JMIDS-22-11989; Revised: 28-May-2022, Manuscript No. JMIDS-22-11989(R); Published: 31-May-2022