Keywords

Cost-Benefit Analysis; Flexibility; Uncertainty; Monte-Carlo simulation; Real Options Valuation, Tunisian highway of M’Saken-Sfax.

Introduction

The Cost-Benefit Analysis is the most commonly used evaluation method for transport infrastructure projects. The Net Present Value, the benefit/cost ratio and the internal rate of return are the main choice criteria applied to the CBA. However, the major problem encountered by this analysis is that it does not take into consideration the uncertainties all along the highway lifetime, namely, the evolution of the users’ needs in terms of traffic demand, the evolution of the socio-economic environment, and the technological changes.

The traditional methods of selecting an investment project such as the NPV or the IRR area better alternative in the future. All the parameters of an investment project are expected to be estimated with a high degree of certainty. The main deficiency of these methods is their inability to precisely predict the cash-flows related to an investment project extending over several years. In fact, the NPV method, for instance suffers fromthree major defects, namely its limited capacity inestimating future cash-flows as well as in determining an appropriate discount rate and its neglect of flexibility as a feature of most of the investment projects.

The Real Options Analysis is a financial approach invented by Myers & Turnbull (1977). The authors defined these options as the possibility to buy real assets in a future favorable opportunity. According to Sick (1995), the Real Options provide the needed flexibility for the managers to make decisions related to the real assets. These decisions may imply the adoption, the abandonment and the exchange of an asset for another or the alteration of the operating characteristics of an existing asset. The Stochastic methods have been recently employed in the Real Option Valuation. Zayed et al., (2002) applied a decision procedure of Markov when selecting a rehabilitation plan between the predetermined decision-making policies. Zhao Tong et al., (2004) presented a multistage stochastic model for the decision making in developing an infrastructure project. According to Levyne & Sahut (2009), the Real Options Valuation emphasizes the notion of uncertainty and the project value corresponding to the sum of the future discounted cash-flows and the option value to invest at the appropriate time. Real-option analysis (ROA) is a technique which purpose is to value flexibility to allow an adaptation to an uncertain future (Dawson et al., 2018). This is a feature which can be included in the traditional Cost-Benefit Analysis. According to these authors, the investment projects are mainly real options deposits which derive from three elements namely; irreversibility, risk and flexibility.

This research study dealt with the decision making in a Tunisian highway project taking uncertainty into account. The highway section linking Sousse to Sfax is 98 kilometers in length. The decision would be based on a non-traditional evaluation method applying the Real Options approach. Furthermore, we referred to the CBA traditional method to develop a new approach which takes into account the uncertainties and risks faced in the project. This approach may be useful in the developed and developing countries, particularly, in the field of highway project evaluation.

The Cost-Benefit Analysis and The Evaluation Of Transport Infrastructure Projects

The Cost-Benefit Analysis is an evaluation method and a support tool to the decision making. It aims at taking into account the costs and benefits generated by the project that the community can bear or perceive. This calculation is the result of an assessment using the monetary referent to aggregate the various elements forming the costs and benefits and enabling us to compare the net social gain of the undertaken project. This analysis is a decision-support tool insofar as the evaluation can guide a decision-maker in choosing among the different versions of the same project. When applied to the public choice, the CBA helps choose the project, the program or the policy with the highest net social benefit. The CBA is widely applied in the transport sector.

In this respect, Glaister (1994) state that the traditional transport investment evaluation mainly focuses on their costs and benefits. According to Ilaria et al. (2020), the CBA is widely applied to endorse the decision process in the field of transport through the evaluation of the social and economic potential impacts of each alternative.

Currently, both the Net Present Value (NPV) in a Cost-Benefit Analysis (CBA), is the main evaluation means for investment decisions about large infrastructure projects in several countries. This is also applicable to the Netherlands when one goes through the recently revised version of the CBA guidelines (Eijgenraam, Koopmans, Tang, and Verster, 2000; Romijn and Renes, 2013). Nickel et al., (2009) state that, on a large scale, the CBA has become one of the most accepted and applied methods in the evaluation of infrastructure projects in the public sector, such as transport infrastructure projects.

In this context, we can also mention several other works dealing with the same issue like those of Leleur (1995), Peaman et al., (2003), Salling & Banister (2009), Calthrop et al., (2010), Adler et al., (2010), (Dawson et al., 2018). The selection, in the field of transport infrastructure, is very complicated. Decision makers have to be able to evaluate the relevance of the project and each possible variable, taking into account the community. This evaluation should be a part of an approach because the transport infrastructure projects are characterized by their long lifespan.

Evaluation, in this respect, is also a hard task to achieve. The calculation of the investment financial costs, the financial receipts, the maintenance costs, the project impacts on the community and the environment, the traveling time, and safety are all very intricate tasks. In an attempt to overcome these difficulties and complexities, the European countries, the United States, Canada among others as well as several international and local organizations offered and developed economic calculation tools of the type of the Cost-Benefit Analysis.

The practice of the CBA applied in road transport was developed in Great Britain. In the 1950’s, the public authorities set up an economic method and a data-processing tool in the planning and construction of the British road network, to compare between the different policies and road transport infrastructures. Since the CBA genesis and up to the last few decades, several methods and techniques have been regularly created and improved. The Cost-Benefit Analysis can take into account, besides the costs and the receipts of the life-cycle, the benefits of the transport infrastructure construction, the time savings, the reduction of the operating costs, the reduction of the pollutants and noise irritations and the improvement of safety, which are all the main externalities of a new highway or road transport infrastructure. This is due to its driving principle, namely the achievement of an objective with available means under several constraints. It is also due to its definition of the object of the economics. The Cost-Benefit Analysis criteria of the investment selection help the decision makers to identify the scenario or the infrastructure project ensuring the maximum return. According to the CBA, the minimum criteria of the investment selection are the Net Present Value (NPV) and the Benefit/Cost ratio (B/C/R).

The Net Present Value presents several deficiencies that require improvements in order to have a more precise and realistic evaluation of the investment project. In order to overcome these deficiencies, several financial and economic studies suggested other methods and techniques such as the optimized NPV, the real options valuation, the Monte-Carlo simulations (MCS) among others

The Optimized Net Present Value (O-NPV)

The O-NPV is an evaluation method for an investment project designed to remedy certain deficiencies of the traditional NPV in the presence of several sources of risk.

A project evaluation must be accomplished through the decomposition of the cash-flows into components corresponding to the different sources of risk and discounting these components using a specific rate for each. The project value is obtained by summing the current values of the diverse components. Alternatively, the different components can be corrected according to their risks in order to obtain their certain equivalents. The project value is the sum of the certain equivalents discounted at the identical, unique, obvious and risk-free rates. Boyer et al. (2005) demonstrate that in the presence of many risks, the use of a unique discount rate combining the risk premium and the time preference (the risk-free rate) violates some fundamental principles of the value creation Brennan et al., (1985). They have also approved of the necessity of an adequate method that consists of decomposing the cash-flows of an investment in terms of risk sources and then calculating the net present value of these components Childs et al., (1999). Even though the O-NPV overcomes the deficiencies of the traditional NPV, it, still, does not take into account the flexibility characterizing the majority of the investment projects. The Real Options Valuation came as the solution for the O-NPV’s deficiencies by considering the above-mentioned factor.

The Real Options Valuation (Rov)

Literature Review

Hertz (1964) were the first theoreticians to incorporate the decision flexibility in the investment projects. Hertz tried to integrate the executives’ decisions concerning the variables of the state of the project based on the Monte-Carlo Simulations (MCS). Magee (1964) used a decision tree in order to incorporate the value of the stochastic variables of the project and the executives’ opportunity to alter the financial flows. The notion of the Real Options appeared in the late 70’s after the works of Black & Scholes (1973) and Merton (1973) that brought along the financial options valuation. Myers (1977) was the first to formalize the concept of the Real Options Valuation. He relied on the works of Black, Scholes and Merton to establish an analogy between the growth opportunity and the call. Banz (1978) applied the arbitrage theory to assess an investment project but they did not envision the decision makers’ actions in order to control the cash-flows. Afterward, Rester (1984) was inspired by the idea of Myers (1977) and determined the analogy between the European call and the growth options. His model is considered as the first endeavor of the type of option of the initiating opportunity of a project. McDonald & Siegel (1985) explained the use of the option to abandon in order to evaluate an investment project. McDonald & Siegel (1986) determined the value of the option to wait. They studied the asymmetry between the decision of investing and postponing and took into account the character of irreversibility. Both of these economists incorporated the cost of the opportunity without waiting for the information on the project development.

In a fundamental article, Brenman and Scwartz (1985) tried to develop an opportune time generation model for a project execution. They incorporated the closure option, the option to wait (deferral option) and the option to temporarily stop producing. Majd & Pindyck (1987) developed a model in which the company invests every single sum to buy the option of spending the next unit until the interruption of the investment. Kulatilaka (1988) succeeded in applying a new option called the input choice option which consists in replacing coal by fuel in the field of power feeding. Myers & Majd (1990) made an analogy between the American put option and the ‘abandon’ option to an investment project. Trigeoris (1993) shows that the implicit values of the option in a project are not always additive. He incorporated the interaction between the options, as well. In 1996, he succeeded in inventing another type of options known as the compound option. A compound option is an option depending on another one Dixit and Pindyck (1994), Trigeoris (1996) agreed that the method of the real options is developed to face the deficiencies of the NPV method by taking into account the dynamics of the investment decision, especially irreversibility and the possibility to postpone an investment project i.e., flexibility. According to McGrath (1999), the real options correspond to applying the financial options’ theory in the real assets. Moreover, the owner of a real option has, in full sovereignty, the right to makea future action and to make certain future or pre-future decisions. As for the mutually exclusive projects, Child et al., (1998) presented a model of the real options valuation taking into consideration the effects of the interdependence between different projects on the decision making of the executives. Triantis & Borison (2001) integrated the notion of the optional approach of the real options valuation which is a universal financial instrument for the assessment of an investment project flexibility. Levyne & Sahut (2009), also, stipulate that the approach of the real options focuses on the concept of Uncertainty. Thus, the value of the project is the sum of the future discounted cash-flows and the value of the option of investing at the most opportune moment.

Godinho (2010) analyzed the use of real options analysis within a cost-benefit framework to find the best timing for starting the construction of road infrastructures. Experimentally, Karami and Farsani (2011) proved that people who apply the ROA budgeting method are less likely than those who adopt the static NPV method to continue a failing project. This was attributed to the improved access to the idea of abandoning the project. Knight and Singer (2012) demonstrated how the real options analysis and simulation can be applied to value flexible architectures in early design stage, given certain assumptions about the dynamics of key input variables like freight rate. Wang et al. (2014) used the real option to solve the car park scale problem. The results show that the real option can significantly optimize the PPP projects decision making process. Several studies were achieved to allow the understanding of the application of real options in infrastructure management (Garvin and Ford, 2012; Kashani, 2012; Martins et al., 2015; van Rhee, Pieters, and van der Voort, 2008).Gijsen (2016) agreed that ROA is valuable as it can enrich the decision-making information for certain Dutch transportation infrastructure projects. Essentially, ROA leads to optimal decision-making and additional strategic insights thanks to its support to an adaptive decision-making. Dawson et al. (2018) used a modified ROA approach to the ex post economic assessment of the management of a notorious section of coastal transport infrastructure in the UK. This method has been praised as an approach to improve economic decision making under uncertainty, allowing flexibility and learning in infrastructure investment. According to these authors, the investment projects are, mostly, deposits for the real options finding their sources in three elements, namely; irreversibility, risk and flexibility.

Conditions of the Existence of The Real Options

Kamrad, (1995) cited three conditions for the use of the real options valuation which are; uncertainty, flexibility and irreversibility Kester, (1984). According to this author, this valuation would bring no further contribution compared to the NPV calculation if the optional logic conditions were not fulfilled. For an investment project, if all the variables are identified with certainty, it will be possible to predict whether this project is profitable or not. In this case, the valuation would bring no further contribution compared to the net present value calculation.

Wernerfelt & Karnani (1987) mentioned four sources of uncertainty that a decision of a strategic investment may face. These sources are; the uncertainty associated with the demand, the uncertainty associated with the supply, the uncertainty associated with the competition and the external uncertainty. The second condition requires the irreversibility of the entire or part of the investment costs. On the other hand, if the financial backers can recover the invested amount, they will invest regardless of the risks and the selection criteria would thus be worthless. According to Henry (1974), a decision will be irreversible if it significantly reduces the possible future choices for a sufficiently long period. The third condition requires that flexibility be part of the investment decision. Flexibility is the opportunity of benefiting from the favorable circumstances and avoiding the adverse ones. Flexibility in an investment project is the main generator of the option values. As a matter of fact, it is the possibility to exercise a real option or abandon it. Hence, without flexibility, the real options are impractical since there would be no opportunities.

On the other hand, from a technical point of view, the SMC does not focus on stochastic MBG-type processes but can integrate other processes. Moreover, as we have previously seen, the Monte Carlo simulation method is a flexible approach of valuing real options because it helps model several uncertainty sources and takes into account properties of the investment decisions.

Models of Real Options Valuation

The most well-known model of the options valuation over a continuous time is that of Black & Scholes (1973). The main deficiency of these models is that the result is an analytic solution depending on binding assumptions. If we drop some assumptions in order to work well with the real options characteristics, the analytic solution will no longer be possible. Thus, it is essential to use the numerical methods for the resolution of the equation.

Cox et al. (1979) developed an option valuation model using the Binomial trees. This method uses the GBM assumptions to discretely model the evolution of the price of the underlying asset. The models, in discrete time, such as the Trinomial and the Multinomial were developed afterwards. These models are more transparent and flexible than those of the continuous time. However, the theoretical basis of the models in discrete time and those in continuous times are identical, which creates a deficiency in the real options valuation. In this context, these models provide a simplified vision of the investment decision and the stochastic process followed by the underlying asset. In the academic literature, the approach of Monte-Carlo Simulations for the real options valuation appears to be deficient. This technique was developed by Copeland & Aantikarov (2001) in order to estimate the volatility parameter. Afterwards, this approach was applied in many study cases such as those of Miller et al., (2004).The valuation of the option approach itself has scarcely been applied. Among the rare works that referred to this approach, we can cite those of Tseng & Barz (2002), Nembhard et al. (2005), Sun & Ertz (2020).

Resorting to Monte-Carlo Simulations for evaluating the real options in these works is due to the flexibility of the approach and its ability to take into account the complexity of the investment decision. Furthermore, the MCS approach enables an easy integration of the stochastic process. On the other hand, this approach allows the valorization of the interacting options and the incorporation of the choice possibility within many possibilities not at maturity.

Monte-Carlo Simulations are performed in four steps to evaluate a European Option. The first step consists in modeling the uncertainty sources of the investment project, starting with the choice and the parameter setting of the distribution law for the main sources of uncertainty and then the determination of the correlation between these sources.

The second step is to simulate the possible values of the project at the maturity of the option. To begin with, the presentation of the future cash flows released by the project must be performed. Then, the MCS is conducted for every simulation to obtain the project value. The third step is about the choice of the strategy in the maturity period and the calculation of the Pay-Off.

Pay-Off=max(Sr-k;0) (1)

where

K: The investment cost necessary for launching the project;

Sr: The value of the cash flows generated by the project if its launching occurs at maturity T.

The last step is the calculation of the option value corresponding to the average of the Pay-off, then its discounting at the current date.

The valorization of the American option appears to be more intricate than the case of the European option since the modeling of the evolution of the underlying asset is achieved at an intermediate date. This modeling determines a distribution law of V at and a distribution law of V at in order to simulate how an uncertain variable V may evolve from to . Then, a correlation between both distributions must be established. The negative correlation coefficient reflects the mean-reverting process. On the other hand, a positive correlation coefficient explains that at ,the value is situated at a high level of the range and at , the value is probably high too and vice-versa. After obtaining the trajectories, we can apply the least squares approach of Long Staff and Schwartz (2001) to calculate the value of the option.

Empirical Study: Real Options Valuation of M’Saken-Sfax highway

The valuation process of the highways, used by the Ministry of Equipment and Housing of Tunisia, does not take into account the evaluation of flexibility. It is the duty of the real options valuation to take into consideration the flexibility in the process of the project decision. In this section, we underlined the contribution of this type of valuation to the assessment of the highway projects. The decision timing is very important for all the transport infrastructure and highway projects, in particular. The importance of the decision timing is due to the huge irreversible financial investments with a limited budget for this kind of projects. Thus, the real options valuation is applicable for these investments. In addition to the decision timing, the highway conception is a primordial issue in the evaluation and is considered as a dynamic decision. However, the evaluation of the highway projects conducted by the Tunisian authorities was founded on the calculation of the net present value with no consideration for the dynamic perspective. For the construction of a two-lane highway taking into account the idea of expanding it in the future into a four-lane highway. If the expansion is too expensive, this scenario will not be an optimal strategy. However, if we adopt some essential expansion elements during the construction of the two-lane highway such as bridges, tunnels and fields on the right, the enlarging scenario would be less expensive. Consequently, if we invest an extra amount of money today, we will be able to expand it afterwards for a low cost when the two-lane highway reaches its limit capacity, in other words, we will acquire the growth option for a subsequent expansion.

In fact, the timing of the decision and the growth decision are interdependent. Our first question is whether to invest immediately or not? The second one is when investing, should we invest in a two-lane or a four-lane highway?

The purpose of this study was to implement a quantitative analysis for the construction of M’Saken-Sfax highway with the option of adding more lanes. In order to reduce the difficulties faced in the calculation, the growth option will be modeled in the form of a European option. This option was applied in a particular determined date. We presented a simulation model based on the Geometric Brownian Motion to quantify the value of the option

Presentation of the Highway

The M’Saken-Sfax highway portion is part of the North-South axis of the highway schema provided by the economic and social development plan of Tunisia. Extending next to the national road NR1, the is approximately 98 km in length. The global costs of the highway construction are estimated at 430.368 million TND. These costs include the crossing structures, the restoration of the communication structures, the resting end service areas and various other required equipments for the highway tolls operation in addition to the intercalary interests.

The achievement of M’Saken-Sfax highway was assigned to Tunisia-Highway Company. The European Investment Bank financed the tax-free costs of the construction of the first section of M’Saken-El Jam estimated at 149,153 million TND. The rest of the highway was financed by the Japan Bank for International Cooperation (JBIC), Tunisia-Highway Company and the Tunisian government. The useful life time of the chosen highway was assessed over a horizon of35-year period. This choice is based on the obvious life time of the highway and its equipments. The exploitation costs are to be calculated over a horizon of 4 years. The optional costs and benefits are to be calculated over a horizon of 31 years. According to the reports of the Tunisian Ministry of Equipment and Housing, the predicted number of vehicles using the highway in its first operational year was, approximately, 48.522 vehicles per month. This number includes heavy vehicles (HV), nearly 7,644, and light vehicles (LV), nearly 40,878. According to the same report, the trend growth of the traffic flows is of the order of +5% per year. These traffic flows have a standard deviation of +4.75% per year Figure 1.

Based on these data, we would decide whether to immediately invest and if we decided to invest immediately, how many extra lanes would be built in the future? The controversy is to choose between a two-lane highway with a quick potential of becoming a saturated road and an underused four-lane highway at higher costs.

Based on the results of the Cost-Benefit Analysis of M’Saken-Sfax highway, the predicted cost of one lane is 80, 250 million TND. We assumed that a two-lane highway may be able to absorb the traffic demand that exceeds its limit capacity. However, the benefits of this extra traffic for the community are null. The economic benefits of a new transport infrastructure are, mainly; time savings, safety gains, and other environmental advantages. Yet, these time gains are null if the traffic congestion is high. The difference in distance between the NR1 section linking M’Saken to Sfax and the highway section linking both of these towns is approximately 22 kilometers. The time saving offered by the project is 43 minutes. The time and travel savings and the reduction of the distance travelled have resulted in cost gains in the exploitation of vehicles which were calculated in accordance with the proportions of LV and HV from the total traffic. After this calculation, the value of the highway exploitation up to its limit capacity was estimated at 7.850 TND. Since the uncertainty associated with the traffic demand is higher than the uncertainty associated with the maintenance costs, we could assume that the costs per vehicle were constant in real terms.

The Model

The investment decision in one highway depends on the future traffic demand. However, it is hard to predict the exact number of vehicles. We can only simulate the future traffic flows. Every distance of the sample exhibits a different history. We established a distribution of the traffic demand for each future point in time. We used the Geometric Brownian Motion (GBM).

Given the expected performance growth designated by μ and the standard deviation represented by σ, the assumption stating that the performance respects a Geometric Brownian Motion provides the solution for the linear stochastic differential equation at constant coefficients.

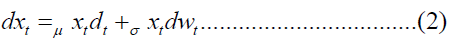
where 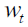is the standard Brownian Motion.

In our study case, the differential equation is written in the following form:

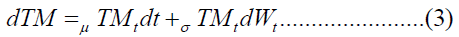
TM: The volume of monthly traffic;

μ: The drift rate;

σ: The volatility measured by the standard deviation;

dWt: The infinitesimal increment in Brownian Motion.

The drift and the standard deviation are multiplied by referring to the level of traffic. This means that the traffic rate follows an arithmetic Brownian Motion:

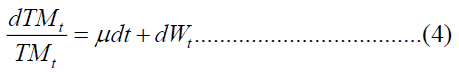
Using the lemma of Itô, the stochastic differential equation (3) provides the following solution:

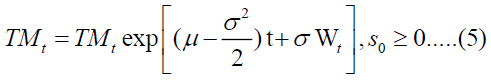
If the stochastic differential equation of complies with a Geometric Brownian Motion, the volume of traffic follows the log-normal distribution and the logarithm of follows a normal distribution. In order to show that this logarithm follows a normal distribution, we applied equation (3) of the highway traffic and a function which is equal to Ιn(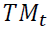). So, this function depends on the random variable . 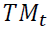According to the lemma of Itô, the differential equation of the function g is written as follows:

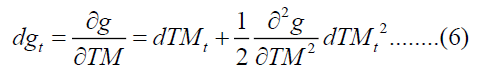
The lemma of Itômatches the second level expansion of Taylor. However;

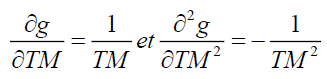
By substituting these derivatives in equation (5) and replacing by equation (3), we obtain:

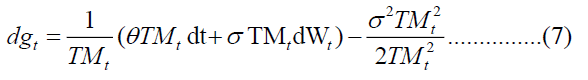
Where 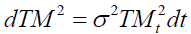After simplifying equation (6), we obtain:

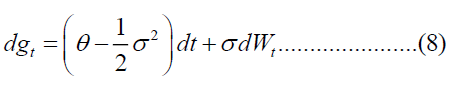
The logarithm of TM_t ,which is the function ,follows a normal distribution since complies with a normal distribution. Therefore, we can write the performance in the following form:

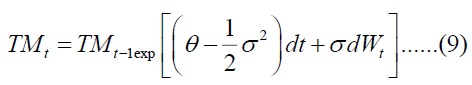
Equation (9) is the explicit solution to the MBG to simulate the trajectories.

Results

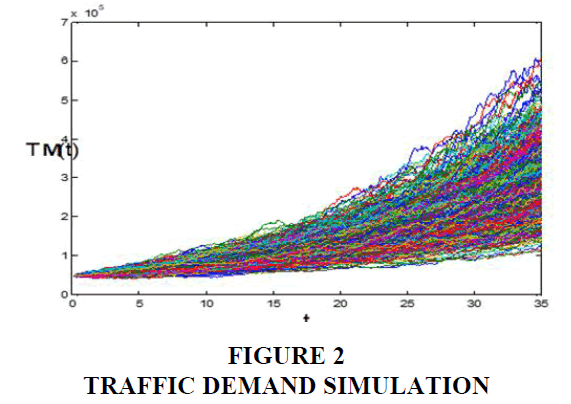
Equation (9) is, then, the explicit solution for the GBM to simulate the trajectories. Figure 2 shows one thousand stochastic simulations of the traffic demand.

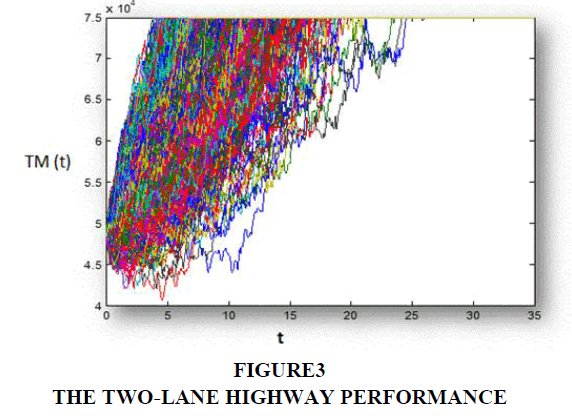
Based on the estimations of the General Directorate of Roads and Bridges, we assumed that the alternative of the two-lane highway is limited to the threshold of 75,000 vehicles per month. Considering this restriction, the benefits of the highway are distributed as indicated in Figure 3.

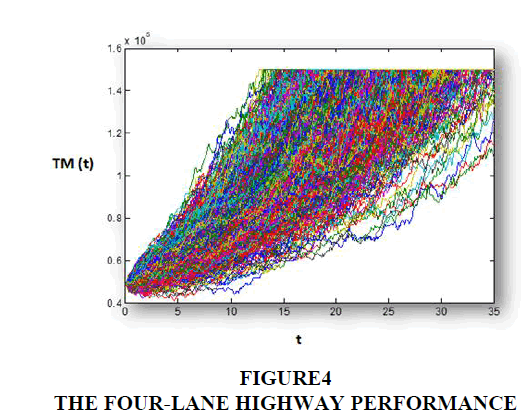
The alternative of a four-lane highway provides a greater capacity for the highway traffic. This capacity would develop rapidly in the years to come. However, Figure 4 exhibits the unused capacities in several cases over a long period. In this optimistic case, the limit capacity is reached in 13 years. However, in many other cases, the additional capacity remains unused.

Considering the results provided in Table 1 (cf. below), the two-lane highway is favored to the four-lane alternative. Moreover, the cost of a weak capacity caused by the lost benefits is inferior to the capital cost of the underused capacities.

Table 1 The Discounted Value of the Two-Lane Highway, the Four Lane Alternative and the Two-Lane Highway with Real Options (TND)
Alternative	Discounted value
Two-lane highway	59, 269,000
Four-lane highway	29, 896,000
Two-lanehighway+Option	63, 559,000

The third alternative, which the flexible one, i.e., the construction of a two-lane highway at the moment and its expansion later to a four-lane alternative would require certain measures such as the purchase of the right-of-way and the construction of bridges and tunnels. This expansion can be achieved in the future only if more information concerning the traffic demand is acquired. According to these results, the alternative of the real options is desirable compared to the other solutions.

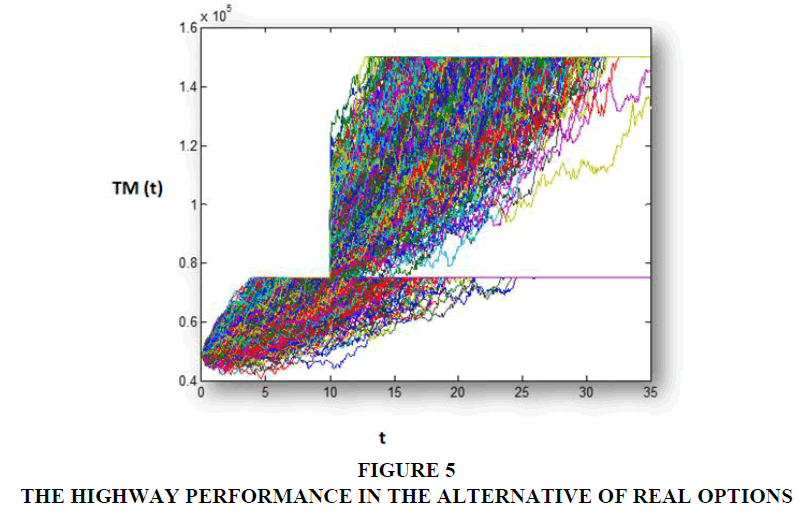
The reason behind this result is that the project did not have the means of financing the unused capacities in its first years. The value of the real option can be divided into two parts; the waiting value and the information value. The first part is the result of the fact that the benefits increase more slowly than the discount rate. Hence, the discounted benefits are inferior to the costs. For this reason, it is optimal to postpone the investments. The second part is the result of the information. We can enlarge the highway when the increase in traffic demand is sufficiently high. If the traffic demand is low, we will never have the probability of applying the option the expansion or growth option. The simulation of the highway performance achieved in the alternative of the real options is shown in Figure 5. And so the value of the option consists of two components, namely; the value of the waiting time for the reduction of the capital costs when the highway is underused and the value of the arrival of information because exercising the growth option or the option to expand depends on the information about the future traffic demand.

In fact, the 3-lane alternative is a basic scenario however, it is not a flexible alternative especially for the traffic frequency. Therefore, based on the Monte-Carlo simulation, we cannot go through the 3-lane alternative because, as the results show, we will go back to the same problems as in the 2-lane alternative.

Thus, our study case analyzed the real options valuation that can be obtained by adapting certain critic elements to the traditional evaluation methods of the highway projects. Hence, a subsequent expansion of the highway section of M’Saken-Sfax is conceivable at a lower cost. The simulation and assessment results show that the real option value consists of two parts; the first reflects the waiting value and the second deals with the information value.

Moreover, the numerical results show that the proposed model is useful for the decision makers owing to its ability to take uncertainty into account and integrate the real options in the evaluation of the highway projects. The total value of the project will increase and provide more accurate information for the decision maker. In addition, this model is more flexible since it highlights the uncertainties compared to other evaluation methods. Each single uncertainty, not considered by the Cost-Benefit Analysis and incorporated in the Real Options Valuation, would have an influence on the project value and the investment decision.

The results obtained by the SMC method (Figure 5) show a ceiling in the traffic demand at year 10. Therefore, if the decision is made before this date, there will be underutilization of the new highway capacity and therefore there will be an unused capacity.

Conclusion

This paper explained how uncertainty, in the evaluation of a transport infrastructure project, can be managed by the real options valuation. The use of the ROV model shows how the evaluation of the projects can be better adapted to uncertainty. The growth option or the expansion option has a considerable value. The flexible alternative is more valuable than the other alternatives which are either the immediate achievement of a two-lane highway or the construction of a four-lane highway in the future. Our study has also shown that the evaluation of risks and uncertainties can be embodied in an expanded form of the Cost-Benefit Analysis. The uncertainty tools can improve the norm of the CBA as shown in the model of the real options valuation. The of the Benefit/Cost ratio evaluation enhancement, through the incorporation of uncertainty, provides a theoretical and empirical process for the management of risks. This process allows the practical implementation of a new principle in the evaluation of big public infrastructures and highway projects, in particular. Such an implementation substantially changes what is considered as the criteria of the evaluation of a Cost-Benefit Analysis.

Nevertheless, many conceptual and empirical questions still need to be answered in future research such as the study of other aspects of flexibility, other than the uncertainty of performance. Among these we may mention the inducible regulation uncertainty, the use of another stochastic motion like the Fractional Brownian Motion or the integration of a Bayesian approach in order to update the state of knowledge at a given time.

References

Banz, H-M. (1978). “Prices for State-Contingent Claims: Some Estimates and Applications”. The Journal of Business, 51(4): 653-672.

Black, F. and Scholes, M. (1973). “The Pricing of Options and Corporate Liabilities”. The Journal of Political Economy, 81(3): 637-654.

Boyer, M., Boyer, M. M., & Garcia, R. (2005). The value of real and financial risk management. Available at SSRN 873356.

Brennan, M-J., and Schwartz, E-S., (1985).”Evaluating Natural Resource Investments”. Journal of Business 58: 135-57.

Calthrop, E., De Borger, B., & Proost, S. (2010). Cost-benefit analysis of transport investments in distorted economies. Transportation Research Part B: Methodological, 44(7), 850-869.

Childs, P-D., and Triantis, A., J. (1999). “Dynamic rand investment policies”. Management Science, 45(10): 1359-1377.

Copeland, T., Antikarov, V. (2001). Real Options-A Practitioner's Guide. New York. Texere Publishing limited.

Cox J, C., Ross S., Rubinstein M. (1979). “Option Pricing: A Simplified Approach”. Journal of Financial Economics, 7: 229-263.

Dawson, D-A., Hunt, A., Shaw, J., and Gehrels, W-R. (2018). “The Economic Value of Climate Information in Adaptation Decisions: Learning in the Sea-level Rise and Coastal Infrastructure Context," Ecological Economics, Elsevier, 150(C), 1-10.

Henry, C. (1974). “Investment Decisions under uncertainty: The Irreversibility Effect”. American Economic Review, 1974, 64: 1006-1012.

Hertz, D-B. (1964). “Risk analysis in capital investment”. Harvard Business Review 42: 95–106.

Ilaria H., Armando C., Clorinda M. and Aussunta E. (2020). “Decision-Making in the Transport Sector: A Sustainable Evaluation Method for Road Infrastructure”. Sustainability Journal. 12(3).

Kamrad, B., (1995). A Lattice Claims Model for Capital Budgeting. IEEE Transactions on Engineering Management, 42(2): 140–149.

Kester, W. C. (1984). Today's options for tomorrow's growth. Harvard business review, 62, 153-160.

Kulatilaka, N. (1988). “Valuing the flexibility of flexible manufacturing systems”. IEEE Transactions on Engineering Management, 35(4):250–257.

Leleur, S. (1995). Road infrastructure plannint: a decision-oriented approach. (No Title).

Levyne, O., & Sahut, J. M. (2009). Options réelles: intégrer risque et flexibilité dans les choix d'investissement. Paris: Dunod, 2009. 297 p.

Magee, J-F. (1964). “How to use decision trees in capital investment”. Harvard Business Review, 42: 79-96.

Majd, S., & Pindyck, R. S. (1987). Time to build, option value, and investment decisions. Journal of financial Economics, 18(1), 7-27.

McDonald, R. and Siegel, D. (1985). “Investment and the Valuation of Firms When There Is an Option to Shut Down”. International Economics Review. , 26, 331-349.

McDonald, R. and Siegel, D. (1986). “The Value of waiting to Invest”. Quarterly Journal of Economies, 101(4): 707-728.

McGrath, R., (1999). “Falling forward: Real options reasoning and entrepreneurial failure”. Academy of Management Review, 24(1): 13-30.

Merton, R-C., (1973). “An Intertemporal Capital Asset Pricing Model”. Econometrica, 41(5): 867-887.

Miller, K-D., Shapira, Z. (2004). “An Empirical test of heuristics and Biases affecting real option valuation”., Strategic Management Journal, 25( 3) : 269-284.

Myers, S. and Turnbull, M., (1977). “Capital Budgeting and the Capital Asset Pricing Model: Good News and Bad News”. Journal of Finance. 32(2): 321-36.

Myers, S., and Majd, S., (1990). “Abandonment value and Project Life”. Advances in Futures and Options Research, 4, 1-21.

Myers, S-C., (1977). “Determinants of Corporate Borrowing”. Journal of Financial Economies, 5(2): 147-175.

Nembhard, D-A., Nembhard, H.B. and Qin,R., (2005). “A real options model for workforce cross-training”. The engineering economist, 50(2): 95–116.

Nickel, J., Ross, A. M., & Rhodes, D. H. (2009, June). Comparison of project evaluation using cost-benefit analysis and multi-attribute tradespace exploration in the transportation domain. In 2nd international symposium on engineering systems.

Salling, K. B., & Banister, D. (2009). Assessment of large transport infrastructure projects: The CBA-DK model. Transportation Research Part A: Policy and Practice, 43(9-10), 800-813.

Sick, G. (1995). Real options. Handbooks in operations research and management science, 9, 631-691.

Sun, S., & Ertz, M. (2020). Life cycle assessment and Monte Carlo simulation to evaluate the environmental impact of promoting LNG vehicles. MethodsX, 7, 101046.

Triantis, A., & Borison, A. (2001). Real options: state of the practice. Journal of applied corporate finance, 14(2), 8-24.

Wernerfelt, B., and Karnani, A. (1987). “Competitive strategy under uncertainty”. Strategic Management Journal, 8: 187-194.

Zayed, T. M., Chang, L. M., & Fricker, J. D. (2002). Life-cycle cost analysis using deterministic and stochastic methods: Conflicting results. Journal of Performance of Constructed Facilities, 16(2), 63-74.