Keywords

Black-Scholes Option Pricing, Bibliometric Analysis, Content Analysis.

Introduction

Since 2000, F&O trading has become a dynamic and substantial part of Indian stock market. The tremendous rise in the trading volume of options and futures has resulted into high volatility and making option pricing more complex. Black-Scholes option pricing model is a scientific pricing model to determine the fair price of the option contracts. Fischer Black and Myron Scholes created this model in 1973, and Robert Merton generalised it to its current form. The Black-Scholes Option Pricing model (BSOPM) is used to evaluate the fair price or theoretical value of a call or put option based on six variables including volatility, option type, underlying stock price, period, strike price, and risk-free rate. Boness (1964) pioneered the current option market structure dates to 1964 and attempted to provide a comprehensive analysis of predicted option values. This empirical insight in option pricing resulted in to increased momentum in 1973 when the Chicago Boards Options Exchange was set up as the first marketplace to trade listed options. However, it got noted widely when seminal research by Black & Scholes (1972) provided a general equilibrium solution for the option pricing. Further, Cox & Ross (1976); Smith (1976); Merton (1973a, 1973b, 1976) reworked on the critiques, applications and improvised on it and provided robustness to the option pricing modelling. Afterwards, there was a series of research by eminent professional of the field; however, majority of them (Hull & White, 1987; Scott, 1987; Wiggins, 1987) assumes zero risk premia. In the current period, due to the availability of large amount of data, technological innovations, and applications (Bates, 2003) have reworked by considering multiple types of risk and attempted to provide empirical research on alternative option pricing models. Similar approach was adopted by (Zumbach, 2012). Similarly, Cox et al. (1985); Stein & Stein (1991); Heston (1993) have further reworked on it by considering alternative ways of risk premia and volatility.

Literature Review

Black & Scholes (1973) stated that the Black-Scholes model explains the price of the heavily traded assets and follows a geometric Brownian motion with constant drift and volatility. Frino & Khan (1991) empirically tested the model by taking large historical data and said that the model is fair. Research by Choi & Wohar (1994) questioned for the mathematical model and said that derivation and solution of the model are advanced and unfamiliar to many researchers and practitioners. Bakshi et al. (1997) stated that the stochastic volatility is the major concern in valuation of options. Kim et al. (1997) studied the effect of implied volatility for ATM put options and concluded that implied volatility estimates derived from BSOPM model was almost like other complex pricing methods. Sharma & Arora (2015) tested the model for selected stocks of NSE and found that the market does not account for market perceptions. Nagendran & Venkateswaran (2015) observed that higher volatility results into higher deviation of the model price and the market price. Panduranga (2013) suggested for the improvement in the existing BSOPM. Khan et al. (2012) recommended to include more new variables like new risk-free rate of interest to make the model robust (Rodrigo & Mamon, 2006).

Genkay & Salih (2003) in BSOPM pricing errors are bigger for deeper OTM options and mispricing is due to volatility. Result by Nilakantan & Sethi (2012) empirically tested and found that BSOPM has certain degree of mispricing and stated that the difference between the fair and actual prices changes due to change in moneyness of options. This confirms with the findings of (Genkay & Salih, 2003). Bonz & Angeli (2010) attempted to test the application and relevance of BSOPM for index options by comparing model prices and real market prices and found that it performed differently before and after the financial crisis. McKenzie & Subedar (2017) concluded that BSOPM is relevant and significant at 1 percent level in estimating value. Findings of McKenzie & Subedar (2017) are contradicting with that of (Bonz & Angeli, 2010).

Research by Mishra (2012) confirmed that BSOPM is robust model and more fitted for valuing Nifty options. Ray (2012) gave similar conclusion and stated that despite few lacunas in BSOPM; the model is fair for valuing options. Rajanikanth & Lakandha (2015) examined the performance of the European call and put options and concluded that these options move in a non-straight manner and gives a chance to investor to profit in the option market. Sethi & Nilakantan (2016) empirically tested for the call options and found that there is a critical contrast between BSOPM price and market price and such deviations are high for OTM options. Kumar & Agarwal (2017) empirically tested historical data and said that call options are highly mispriced by the BSOPM and advocated for another model for estimating options

In the present study, we evaluated publications on the testing of the BS model in various stock markets throughout the world. Then, we gathered publications comparing the BS model to several option pricing models using Dimensions database. Next, we thoroughly analysed all research papers that contained generalisations or modifications to the classical BS model. Finally, we looked at the total publications, key words, authors, citations, co-authors, co-citations, bibliometric analysis, and country wise analysis and examined the data till 2022 including the most recent research papers.

We are attempting to address the following questions for the research related to Black-Scholes option pricing model (BSOPM).

Research Questions

1. What is the yearly trend of the publications?

2. Who are the authors with the maximum number of research papers?

3. Who are the authors with maximum citations?

4. What are the major clusters within the domain of Black-Scholes option pricing model (BSOPM)?

Research Methodology

Study based on Bibliometric analysis has captured the consideration of the researchers recently (Donthu et al., 2021, 2020; Kumar et al., 2022). Such attention is due to the capacity to handle an enormous amount of data and suitability of various softwares like Gephi, VOSviewer; various data sources such as Scopus, Web of Science, Dimensions etc. Bibliometric analysis helps to unfold the current trends of a journal or a topic; its authorship structure, citation trends and to demonstrate the intellectual structure of a specific field (Donthu et al., 2021). The Bibliometric methodology helps in investigating the performance of a research field. It undertakes a retrospective review of the literature and presents the art of the specific research topic (Baker et al., 2021; Kumar et al., 2022; Mukherjee et al., 2021, 2022; Viglia et al., 2022).

Dimensions is a comprehensive database like Scopus and Web of Science and offers a wide variety of filtering options, providing options to select the data which one wants. At dimensions more than 106 million publications with more than 1.2 billion citations are openly accessible at app.dimenions.ai.

A trio of systematic literature review (SLR), bibliometric and content analysis was applied to address the above-mentioned research questions. Through Bibliometric analysis various assessing and interactive techniques which perform statistical analysis of various research studies are performed (Chen et al., 2016; Bhatt et al., 2020; Gonzalez-Torres et al., 2020). To start with SLR was applied to retrieve the relevant literature. For that firstly keywords were defined and based on that search was performed; various inclusion and exclusion criteria like year, researchers, research categories, publication type, source title, journal list, open access etc were applied to come to the confined research studies conducted for option pricing by using Black-Scholes Model (Kumar et al., 2020). In a second stage, various bibliometric techniques for mapping the literature were applied to get insights like chronological trends of the publications, most prolific authors, leading journals, most influential studies etc (Ren et al., 2019; Eduardsen & Marinova, 2020; Singh & Walia, 2020). Further, content analysis was performed to summarize the findings of these research studies under different categories.

This holistic amalgam of data analysis helps to carry out critical evaluation of relevant literature along with insights to locate limitations and identify research gaps. As per the authors’ best knowledge, this is the first type of study for option pricing using Black Scholes model by applying qualitative tools.

The prime objective of this study is to map the knowledge structure for option pricing by using Black-Scholes model. Bibliometric analysis provides very important information about evolution of a specific field (Baier-Fuentes et al., 2019). SLR is conducted with predefined search protocols, which enhances the quality of the relevant literature considered with attributes of methodical study and comprehensiveness (Pittway, 2008). This thoroughness in the SLR also omits the chance of inclusion of irrelevant studies. This process for conducting literature search is elaborated underneath.

Database, Keywords and Inclusion Criteria

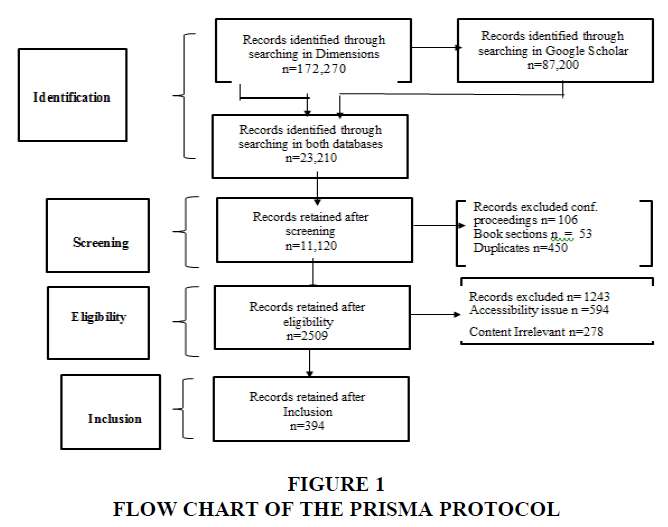
Research work carried out and published in Option pricing by using Black Scholes model is a pool of existing knowledge. The references cited indicate the key variables identified, researched and various relationships established (Mallawaarachchi et al., 2020). The literature search in this paper focuses on the research conducted for Black Scholes Option Pricing Model. The sample of the study is considered from January 1979 to May 2022. Dimensions are used as a database to search for the existing relevant literature in the given area. There were 172,270 articles found in Dimensions on the topic option pricing and Black Scholes model for a period mentioned; out of this most relevant 2509 papers (only journal articles) are considered for the present study. Further, screening criteria named, citation index was applied and only those papers whose citation index is above 25 are considered for the study. Based on this, finally 394 papers were studied.

To avoid any avoidance of certain relevant literature in this area, three stage scrutiny was applied while doing SLR. This three-stage scrutiny was i) Searching by relevant key words, ii) Abstract review and iii) Reference and citation checking (Eduardsen & Marinova, 2020). Similarly, while doing bibliometric analysis, it was taken care regarding appropriate key words. The present study has identified the appropriate search terms by analysing the frequently used key words from peer reviewed literature. By taking inputs from the Chen et al., (2016); Singh & Walia, (2020); the selected database was searched with selected key words and divided the keywords in to following categories. The category of key words includes words related to Option pricing such as “Option Pricing”, “Option Valuations”, Black-Scholes Option Pricing Model, Black-Scholes Model, Black-Scholes Equation, Time-Fractional Black-Scholes Model, Black-Scholes Formula, Monte Carlo Simulation, Weighted Finite Difference Methods, American Option, European Option, Put-call parity, Derivatives, Non-Linear Black-Scholes type model, Risk Sensitivities, Interest Rate Parity Condition, Artificial Intelligence, Machine Learning. Only those research papers were extracted that had above mentioned search terms in the title, abstracts, and keywords.

Inclusion / Exclusion Criteria

While performing the search; the following inclusion/exclusion criterion was applied.

1. The present study considered research papers published in peer reviewed journals in English only. All the papers related to other languages are excluded from the purview of this search.

2. The present study published papers in the peer reviewed journals of Scopus and above.

Selection of the Studies

During the search process of research studies, snow-ball technique was also applied to eliminate the chances of not considering certain papers of this field. For that forward and backward citations were referred. The inclusion criteria provide a broad, consistent, and conversant base of studies to consider (Bhatt et al., 2020).

Bibliometric Analysis

Bibliometric techniques allow researchers to put together their findings regarding collected bibliographic data produced by the researchers working in the area and express their findings through writing, citations, and collaboration. When this information is compiled and examined; it further advances into field’s structure and topical concerns.

Researchers are not required to describe the relationship they seek to investigate, which increases neutrality while examining literature (Garfield, 1979). Second, science mapping entails categorising and visualising past research (Small, 1999). This results in a spatial representation like a geographic map that can show how knowledge areas and particular research are related to one another.

These bibliographic methods have two main applications: results estimation and scientific visualization. Through this, efforts and effectiveness of individual and organizational research is evaluated. Scientific visualization explains the nature and complexities of scientific areas. The insight about structure and evolving growth is useful for researchers if the goal is to review a particular line of study. This bibliographic method adds a methodological rigor to the subjective assessment of the literature. In the context of the calculation of the various bibliometric indicators, the most used approaches are the full counting method and fractional counting method.

In the case of full counting method, a publication co-authored by n researchers is assigned to each researcher with a full weight of one; while in fractional counting method, the publication is assigned to each researcher with a fractional weight of 1/n. In other words, in full counting method all the co-authors are given full weight and overall weight of a publication is equal to the number of authors of the publication and in fractional counting method, overall weight of the publication is equal to one (Perianes-Rodriguez et al., 2016). The present study has used full counting method for all bibliographic indicators.

Here an attempt is made to briefly describe most prevalent bibliographic methods like citation analysis, co-citation analysis, co-authorship, bibliographic coupling, etc. Co-authorship data are used to assess collaboration in co-authorship research.

Search String

To gain important insights from the data, the current study employed a variety of evaluative and relational bibliometric methodologies. A variety of software packages have been utilised in various studies to undertake bibliometric analysis. Each piece of software is considered to have its own set of benefits and drawbacks. BibExcel, Publish or Perish, Bibliometrix R, HistCite, CiteSpace, Eigenfactor Score, Pajek, and Scholarometer are some well-known software tools.

The software package VOSviewer was used in the study due to their high degree of adaptability in changing and updating the input data imported from Dimensions (Persson et al., 2010).

The systematic literature review (SLR) is commonly used in existing literature reviews. SLR is a method for synthesising a large volume of research and determining research progress and gaps, which is used in conjunction with the preferred reporting items for systematic reviews and meta-analysis (PRISMA) protocols (Moher, 2009) which provide clearer and less biased review process guidance (Petticrew, 2008). This review’s PRISMA protocol is illustrated in Figure 1.

Yearly Publication Trend

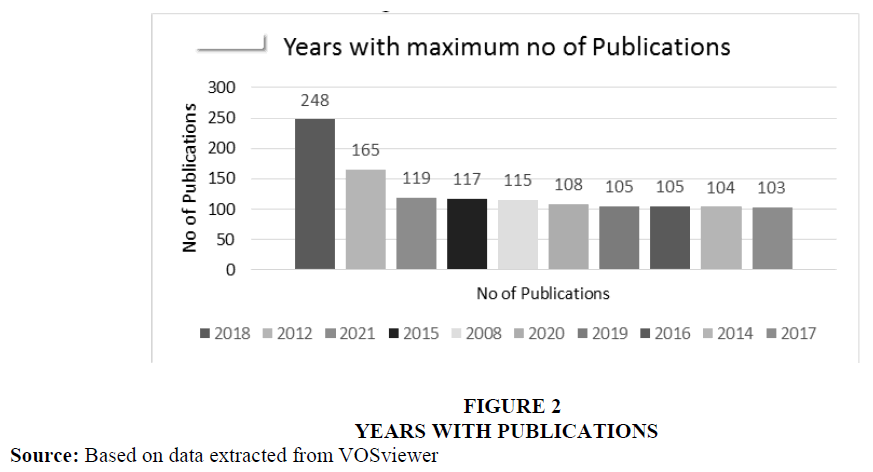
Table 1 and Figure 2 shows yearly publication trend in bibliometric survey on the publications data from the Dimensions database. It is observed that the publication trends are up-down in nature and highest publication in the present research studies are in the year 2018, followed by 2012 and 2021. This is number of articles published on the topic Black Scholes Option Pricing model.

Table 1 Years with Maximum Publications
Year	No of Publications
2018	248
2012	165
2021	119
2015	117
2008	115
2020	108
2019	105
2016	105
2014	104
2017	103

Authors Influence

From the input data file, the author field was derived, and the citations of each author were analysed.

Table 2 provides the summary of the top ten contributing authors and the number of papers they authored or co-authored along with total citations and average citations per article. Data analysed reveals that Kris Jacobs is the most influential author dominating the list. Another noteworthy point is that he also has the maximum number of citations with the average citation of 37.73.

Table 2 Authors with Maximum Number of Documents / Articles
Author	No of Articles	Total Citations	Average Citations
Jacobs, Kris	15	566	37.73
Christoffersen, Peter	14	563	40.21
Core, John E.	9	535	59.44
Schoutens, Wim	9	66	7.33
Turvey, Calum G.	9	209	23.22
Bakshi, Gurdip	8	201	25.13
Bloch, Daniel Alexandre	8	10	1.25
Muhle-Karbe, Johannes	8	25	3.13
Nikkinen, Jussi	8	114	14.25
Boyle, Phelim P.	7	156	22.29

Table 3 below shows the list of top ten authors with highest citations. The author with maximum citations in black scholes option pricing model is Ross Stephen and the number of articles is six. His average citation per article is 604.83. Guay Wayne has the second highest citations with an average citation of 210.83. Ashwath Damodaran is the tenth in the list with 113 citations.

Table 3 Authors with Maximum Number of Citations
Author	No of Articles	Citations	Average Citation
Ross, Stephen A.	6	3629	604.83
Guay, Wayne R.	7	1476	210.86
Jacobs, Kris	15	566	37.73
Christoffersen, Peter	14	563	40.21
Core, John E.	9	535	59.44
Turvey, Calum G.	9	209	23.22
Bakshi, Gurdip	8	201	25.13
Boyle, Phelim P.	7	156	22.29
Nikkinen, Jussi	8	114	14.25
Damodaran, Aswath	7	113	16.14

Treemap below Figure 3 provides the summary of the top ten contributing authors and the number of total citations (MacBeth & Merville, 1980).

Bibliographic Coupling

"Bibliographic Coupling" was one of the first citation analysis approaches for determining document similarity. M.M. Kessler of Massachusetts Institute of Technology (MIT) pioneered the notion. The liaison between the two referencing papers when referring to the common work is referred to as bibliographic coupling (s). A higher coupling strength is shown by a high number of shared citations referenced by the two publications. The similarity of the subject matter is also indicated by bibliographic coupling.

It can be said that the coupling strength is higher when more citations, the two referring works have in common. This coupling determines the subject similarity between the two works. Bibliographic coupling is equally valuable in the fields of research, and it helps the researcher to find the research done in the past on the particular topic or area.

Even though there are various approaches for mapping the intellectual structure of a field, such as co-citation analysis and citation analysis, these methods fail to discover developing themes (Boyack & Klavans 2010; van Oorschot et al., 2018).

Figure 3 depicts the bibliographic coupling of the top 194 cited works on option pricing by using Black Scholes model. The publications are highlighted based on the quantity of recurring citations. The various node colours represent the results of applying the Louvain group identification algorithm on the bibliographic matrix. Community detection algorithm was applied which led to formation of four varied clusters Figure 4.

To answer our fourth research question (i.e. what are the major clusters within the domain of Option pricing and Black Scholes model?), we conducted bibliographic coupling using VOSviewer. In this analysis, the unit of analysis can be the author, document, or countries. We selected author as the unit and full counting as the analysis method as per (Perianes-Rodriguez et al., 2016). The minimum threshold for the number of articles per document was set to 4, minimum number of documents per author was set at 3 and the minimum number of citations of an author were set at 2, which resulted in 194 documents, out of which 187 were linked together. Five clusters were retrieved from this analysis. Table 1 reports the details of the articles retained in each of the five clusters with their citations, links, and total link strength.

The cluster analysis and manual reading of papers in the different clusters gave insights into the inter and intra cluster relationships. There are significantly 5 clusters, which are distinguished by the theoretical concepts, the area, the methodology used and interrelation among the papers. In the red cluster and blue cluster also, there are some papers thought connected but far from the closely related points (Bulan, 2005; Makhudu, 2011).

The cluster analysis and manual reading of papers in the different clusters gave insights into the inter and intra cluster relationships Similarly, “pricing of options” and “Black Scholes model” were referred to in papers in almost all the clusters. Besides these inter-cluster comparisons, the intra-cluster insights included the similarity in themes and methodology besides correlated citation networks. Due to the segregation of papers, the clustering helped in the easy mapping of research. It also facilitated developing a pool of ideas, a few of which highlighted the gaps in extant literature that can be explored further (Alan et al., 1990).

The first cluster (red colour) includes the work of (Madan, 2017; Carvalho, 2010; Anderson et al., 2015). The second cluster (green colour) includes papers by (Christoffersen & Jacobs, 2001) Figure 5.

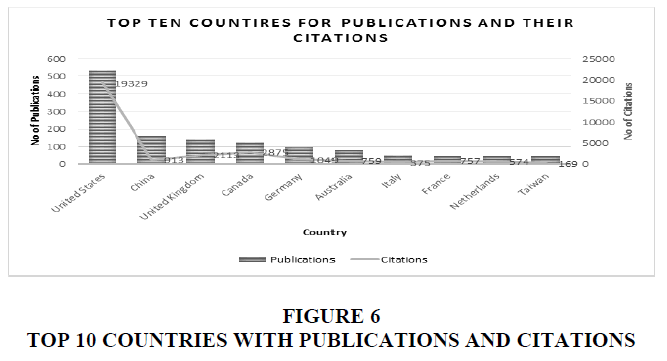
The map above shows the countries with maximum documents. United States has 533 documents / articles on the topic option pricing using black Scholes model. While China and UK stand as countries with second and third highest number of publications. The other countries with maximum publications are Canada, Germany, Australia, Italy, France, Netherlands and Taiwan.

The chart above Table 4 and Figure 6 shows countries with maximum publications and their citations. USA has maximum publications 533 and the total citation for these articles is 19329. Canada stands second in terms of citations though it stands 4th in the number of publications, Taiwan stands 10th in terms of publications but its articles are cited 1690 times and stands 3rd.

Table 4 Top Countries with Publications and Citations
Country	Publications	Citations
United States	533	19329
China	162	913
United Kingdom	139	2113
Canada	126	2875
Germany	101	1049
Australia	79	759
Italy	51	375
France	47	757
Netherlands	47	574
Taiwan	47	169

Co-authorship and Author

It is examined from the below table that there are predominantly four categories for author and co-authorship analysis namely based on documents, citations, total link strength and average citation. In term of highest documents in Black Scholes option pricing model, Jacob Kris leads while Ross Stephen has a highest citation as well as average citation. Authors, Turvey Calum G; Core John E; Madan has good number of documents but do not fall in top five citation and average citation category. Christoffersen & Jacobs (2001) has second highest number of documents as well as leads in terms of total link strength. The term named ‘total link strength’ indicates the number of publications in which two keywords occur together. It is considered as the stronger connections with more links between two items Table 5.

Table 5 Co-Authorship and Author
Rank	Author	Documents	Author	Citations	Author	Total Link Strength	Author	Avg Citation
1	Jacobs, Kris	15	Ross, Stephen A.	3,629	Christoffersen, Peter	19	Ross, Stephen A.	605
2	Christoffersen, Peter	14	Guay, Wayne R.	1,476	Jacobs, Kris	19	Kedia, Simi	315
3	Turvey, Calum G.	9	Kedia, Simi	944	Nikkinen, Jussi	9	Aı̈t-Sahalia, Yacine	287
4	Core, John E.	9	Galai, Dan	903	Li, Zhe	9	Galai, Dan	226
5	Schoutens, Wim	9	Aı̈t-Sahalia, Yacine	862	Liu, Yong-Jun	8	Guay, Wayne R.	211

Co-Authorship and Country

Co-authorship is a metric that tracks scientific collaboration and relationships across networks, teams, institutions, and countries. It is a result of a collaboration between organizations and officials from many countries taking part in a study project. Such research establishes relations among researchers, institutions, and countries. Individual contributor’s number of links can be identified, measured, and shown using co-authorship (Fonseca et al., 2016).

Co-authorship is regarded as an effective tool for scientific collaboration in research publications and it is one of the most concrete and well-known methods of collaboration. Through this, any component of research collaboration networks can be traced (Aldieri et al., 2018; Razera, 2018).

Based on the data retrieved, the global research network in Black Scholes option pricing model was composed of 33 countries, which presents the solid international collaborative research efforts in this field. The top three most central countries, as per their degree centrality are United States, Canada and United Kingdom as represented by the larger nodes (Figure No. 7) For the given period considered for the study, these countries have collaborated with 152, 81 and 64 partner countries respectively Table 6.

Table 6 Co-Authorship and Country
	Country	Documents	Country	Citations	Country	Total link st gth	Country	Avg
1	United States	544	United States	23,429	United States	152	Israel	64
2	China	169	Canada	3,054	United Kingdom	81	United States	43
3	United Kingdom	146	United Kingdom	2,265	China	73	Canada	23
4	Canada	130	Germany	1,119	Canada	64	France	18
5	Germany	103	China	973	Australia	40	Belgium	17

Co-authorship and Organization (university)

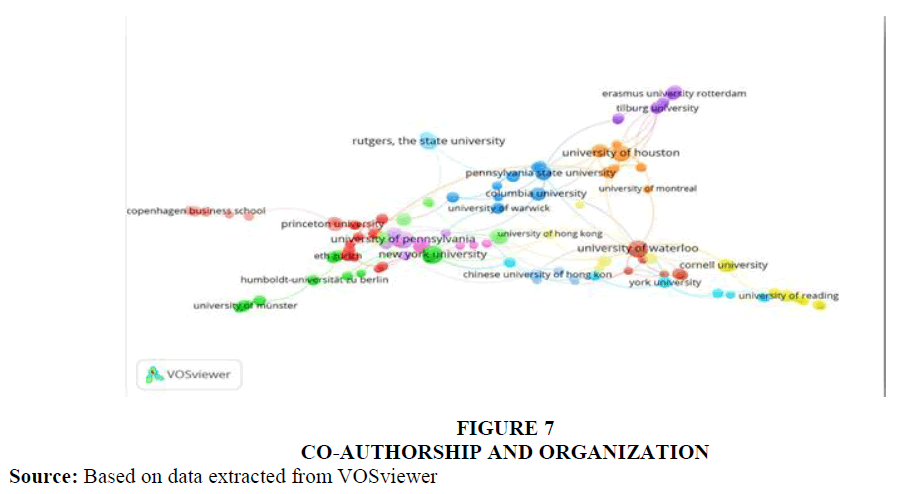
Co-authorship analysis is known to determine patterns of collaboration in a field and network of researchers and relationship among them. The Table 7 and Figure 7 present visualizations of the university co-authorship networks using full counting method. In the figure, each circle represents a university and to avoid overlapping of the universities name, names are shown only for a subset of the universities. The size of the circle reflects the number of publications of the corresponding universities. In other words, the closer two circles are related to each other, the stronger the co-authorship link between the universities. Colours indicate the clusters of universities with strong co-authorship links; lines show the co-authorship links between universities and the distance between two circles approximately shows the strength of the co-authorship link between the corresponding universities.

Table 7 Co-Authorship and Organization
	Organization	Documents	Organization	Citations	Organization	Total Link Strength	Organization	Avg Citation
1	New York University	27	Massachusetts Institute of Technology	4,268	University of Houston	17	Stanford University	388
2	University of Pennsylvania	25	Stanford University	4,267	University Of Waterloo	17	University of California, Berkeley	374
3	University of Waterloo	24	University of California, Berkeley	3,744	McGill University	12	Massachusetts Institute of Technology	328
4	Rutgers, The State University of New Jersey	21	University of Pennsylvania	3,118	New York University	12	University of Chicago	184
5	University of Illinois Urbana-Champaign	20	Princeton University	1,561	Chinese University of Hongkong	11	National Bureau of Economic Research	173

Below table shows the presentation of the co-authorship and university network based on documents, citations, total link strength and average citation of top five universities. For the chosen area of black-Scholes and option pricing; in term of number of documents New York University is ranked number one followed by University of Pennsylvania, University of Waterloo, Rutgers-the State university of New Jersey and the University of Illinois. Massachusetts Institute of Technology and the Stanford University has the highest number of citations followed by University of California, University of Pennsylvania, and Princeton University. In term of average citation, Stanford University is leading even if it does not come under top 5 universities with highest documents. Chinese University of Hongkong is the only university outside US Zone which stands at the fifth position in terms of total link strength. From the below table and figure, it can be inferred that for Black-Scholes Option pricing model US universities are more prominent.

In this figure 7, the visualization shows a very clear pattern, for positioning and clustering of the universities. A few distinct groups of the universities are visible and to a large extent, universities turn out to be grouped by country. From the visualization, it is found that US universities are located towards centre and left of the figure, while Chinese universities are in the bottom area.

This visualization suggests that research-based collaboration mainly takes place mostly within national borders.

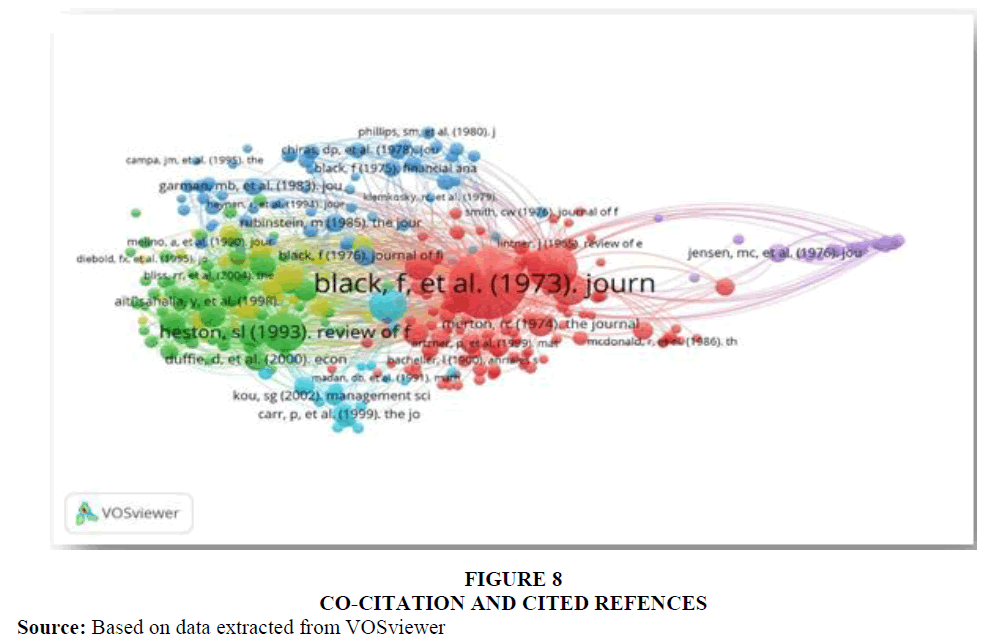
Co-citation with Cited Authors and Cited References

Citation rates evaluate the impact of documents, authors, or journals; and through co-citation journals, documents, and authors are connected based on the joint presence in the reference list. Co-citation is defined as the frequency with which two documents are cited together and co-citation analysis helps researchers to classify scientific literature and gives an idea about the evolution of a certain research field (Surwase et al., 2011).

In other words, it is used to identify, trace, and visualize the intellectual structure of a research field by counting the frequency in which any work of an author is co-cited with another author in the references of citing it (Alan et al., 1990).

By identifying which papers cited with which pairings of articles, co-citation analysis is used to identify links between articles. This strategy is based on the idea that when two publications are cited in other articles, they are more likely to have similar research backgrounds.

The most popular and well-validated bibliometric approach for connecting authors, publications, and journals is co-citation. Co-citation is not the best method for mapping research fronts because it is done on cited papers only. It is not possible to map articles that are infrequently cited because it takes a long time for citations to accrue, fresh publications can only be linked by knowledge base clusters, and mapping requires multiple citations. This helps to filter out most important work Table 8.

Table 8 Co-Citation with Authors and Cited References
	Author	Citations	Author	Total Link StrengthCo-Citation and Cited Authors	Total Link Strength for Co-Citation and Cited References
1	Black, Fischer	1,274	Black, Fischer	37,925	43,216
2	Scholes, Myron	1,039	Merton, Robert C.	30,876	35,379
3	Merton, Robert C.	977	Scholes, Myron	28,947	32,996
4	Ross, Stephen A.	662	Ross, Stephen A.	27,549	30,898
5	Rubinstein, Mark	598	Rubinstein, Mark	23,008	25,602

Co-citation is the frequency in which two documents are cited together by other documents. In other words, co-citation means at least one other document cites two documents in common and the more co-citations two documents receive, the higher their co-citation strength and more likely they are semantically related. Additionally, it is noticed that research works which have already gained much credit and reputation in a particular area/field receives more recognition and citations in future research studies (Trujillo & Long, 2018). As Black and Scholes and Black Scholes and Merton were pioneers in the option pricing theories; Black, Scholes and Merton have highest co-citations of 1274, 1039 and 977 respectively as well as total link strength for co-citation and cited authors and co-citation and cited references.

From the below figure 8 too, same inference can be derived as most of the researchers have cited research work of Black, Scholes and Merton either directly or through cross-referencing.

Content Analysis/Research Synthesis

Content analysis is one of the research approaches to present and analyze the contents of previous studies in actual, methodical and qualitative manner (Berelson, 1952). For this study, narrative synthesis approach is applied in which actual content of previous studies are used to classify literature (Zupic & cater, 2015; Eduardsen & Marinova, 2020). In content analysis, authors found various themes of option pricing like Black-Scholes model of option pricing, Investor sentiments and its impact on option pricing, monte carlo simulation, volatility in stocks and asset pricing. The other categorization based on method, topic, objectives are given in the below Table 9.

Table 9 Black-Scholes Option Pricing Model
Sr. No.	Category	Areas
1	Theme	Black-Scholes option pricing model
		Investor sentiments and its impact on option pricing
		monte Carlo simulation
		volatility in pricing
2	Method for study	Qualitative
		Quantitative
		Conceptual
		Qualitative and Qualitative
		Case study
3	Topics	Black-Scholes model
		Black-Scholes Merton model
		Volatility Analysis
		Arbitrage in assets pricing
		Option pricing using volatility
4	Objective	Empirical study
		Conceptual
		Case study
		Literature review

Black-Scholes option pricing model assumes some crude assumption like absence of transaction cost and dividends, efficient market, risk-free rate for borrowers and lenders etc (Black & Scholes, 1972, 1973; Merton, 1976). Even if these assumptions are far from the real world, there is a widespread acceptance of the model.

As the Black-Scholes-Merton formula calculates the option price, the Monte Carlo simulation enhances the accuracy of the method used. Simulation is run to calculate the price of options dependent on more than one underlying asset. As per Boyle (1977) and Hull & White (1987) factors such as basic Gauss-Weiner process, number of jumps and the amplitude of these jumps govern the distribution of stock prices. Moreover, it assigns probability distribution to each outcome to determine the possible outcome with the highest probability of occurrence which helps to assess the risk and uncertainty associated with the investment. As per Carmona et al, (2012), it provides best and the worst scenarios along with default risk analysis. Longstaff & Schwartz (2001); Fernandez et al. (2013) used it to calibrate various parameters like Alpha, Beta and Rho etc. Das & Padhy (2017) tested Black–Scholes–Merton and Monte Carlo Simulation versus nonparametric machine learning models

Volatility measures the dispersion in prices and a higher volatility means higher swing in the asset prices. The expected volatility signals about the position of the size of the investment and can also cause short fall in margin requirements. It also gives an indication to active investors about where to enter and exit. It is the central part of the Black-Scholes-Merton Model, and it was studied by Chaudhary (2017) and concluded that asset beta, volatility, moneyness and maturity of the option drives the direction and magnitude of the option. Study by Christoffersen & Jacobs (2001); Markellos & Psychoyios (2017) concluded that short term interest rate risk reduces when the maturity rises to a substantial level. Further, authors developed a model to demonstrate the quadratic variation of a stochastic price process. Research by Cao & Han (2013) found that return on equity option decreases in a monotonic way when the volatility trend is up.

In common term, asset pricing means mechanism of “general equilibrium asset pricing” which is usually based on the supply and demand mismatch or rational pricing. In option pricing, “general equilibrium option pricing” means devoid of any arbitrage with respect to the price of the underlying asset. Black-Scholes, Garman-Kohlhagen, Heston etc have applied various risk-neutral asset pricing strategies. These models are useful to price single assets opposed to the basket of assets.

Study by Han (2007) indicated that the index option volatility smile has a higher gradient, and the risk neutral skewness of monthly index returns has a negative return in consonance with the market sentiment and this makes the trend bearish. Study by Brown & Cliff (2004) said that investor sentiment does not impact near term returns which are in contradiction to study by Han (2007). Most prominent economic theory like rational choice theory (Arrow, 1986), nudge theory (Parkinson et al., 2014) revolves around rationality which is far from the real world’s investor actions. Bollen & Whaley (2004) empirically tested and found that implied volatility and net buying pressure are directly correlated. Jackwerth (2000) said that mispricing in option pricing, display an alpha in returns, possibility of further crashes largely affects investors’ sentiments. Research by Baker said that investors sentiments do not allow arbitrage opportunities. Sheu & Wei (2011) found negative correlation between volatility and investor sentiment. This was further confirmed by (Zheng, 2015; Saade, 2015).

Conclusion

The present structured review aims to organize and synthesise the existing literature on Black – Scholes option pricing model. Fisher Black and Myron Scholes introduced the first entirely equilibrium option pricing model pricing approach in 1973. Many researchers later extended the Black Scholes model in various keyways, with the intention of fitting in unique circumstances. The black Scholes model was the first and most well-known option model. The black Scholes model is most suited for pricing European-style options, but it can also price American-style call options with no dividend payment on the underlying equities.

A substantial body of empirical evidence suggests that the black Scholes model, which assumes asset returns follow a continuous diffusion process with constant conditional volatility, is incompatible with the statistical features of many asset prices. The implied volatilities obtained by reversing the Black-Scholes model are larger for deep in the money and out of the money options, indicating a mispricing problem. Researchers also discovered that the Black Scholes Model most certainly overpriced short-term options.

Most of the articles are from the journals: International Journal of Financial Studies, Fuzzy Optimization and Decision Making, Computational and Applied Mathematics, Computers and Mathematics with Application, Applied Mathematics and Computation, Finance and Stochastic, Journal of Financial Economics, Journal of applied economics, Risk etc.

The current work gives a structured assessment of the literature on option pricing using the Black Scholes model, utilising a combination of bibliometric and content analysis. We attempted to find annual trends in publication, geographical locations of all contributing organisations, contribution of organisations based on geographical regions, journal quality analysis, citation analysis, author influence, and keyword statistical analysis using bibliometric analysis. The current study illustrates an evolution of influential publications and contributes to the study on option pricing and Black Scholes model by establishing deeper connections between the higher impact works.

Limitations of the Study and Scope for Future Research

Like many other studies, this study is also not free from limitations. The first limitation is related to the source of data extraction. The study retrieved the data from Dimensions and tried to extract only those research studies which are Scopus and above indexed and whose citations are above 25. Immense care was taken to minimize error in data cleaning; but errors may be in the inbuilt in the source might have affected analysis and outcome.

The study has certain limitations, and it also offers some directions for the future research. The study has used Dimensions database for the search. Multiple databases can provide more information. The current analysis excluded 'grey literature,' such as non-peer reviewed journals, books, and conference proceedings. Inclusion of these materials may provide useful insights.

From the experience, we would like to suggest to future researchers to use multiple datasets to retrieve the data or use Scopus or Web of Science in case of quality research articles. We have remained confined to only Black-Scholes model for option pricing, future researchers can remain open to any valuation technique for option pricing. This will provide further insights for theme based systematic literature review and bibliometric reviews to get better understanding of each option-based pricing theory separately and independently.

References

Alan, E., & John, C.S., & Gerald, W.M. (1990). Mapping intellectual structure of a scientific subfield through author cocitations. Journal of the American Society for Information Science (1986-1998), 41(6), 444.

Indexed at, Google Scholar

Aldieri, L., Kotsemir, M., & Vincie, C.P. (2018). The impact of research collaboration on academic performance: An empirical analysis for some European countries. Socio-Economic Planning Sciences, 62, 13-30.

Google Scholar, Cross Ref

Baier-Fuentes, H., Merigó, J.M., Amorós, J.E., & Gaviria-Marín, M. (2019). International entrepreneurship: a bibliometric overview. International Entrepreneurship and Management Journal, 15(2), 385-429.

Indexed at, Google Scholar

Baker, H.K., Kumar, S., Goyal, K., & Sharma, A. (2021). International review of financial analysis: A retrospective evaluation between 1992 and 2020. International Review of Financial Analysis, 78, 101946.

Indexed at, Google Scholar, Cross Ref

Bakshi, G., Cao, C., & Chen, Z. (1997). Empirical performance of alternative option pricing models. The Journal of finance, 52(5), 2003-2049.

Google Scholar

Bates, D.S. (2003). Empirical option pricing: A retrospection. Journal of Econometrics, 116(1-2), 387-404. \

Indexed at, Google Scholar, Cross Ref

Berelson, B. (1952). Content analysis in communication research.

Indexed at

Bhatt, Y., Ghuman, K., & Dhir, A. (2020). Sustainable manufacturing. Bibliometrics and content analysis. Journal of Cleaner Production, 260, 120988.

Indexed at, Google Scholar, Cross Ref

Black, F., & Scholes, M. (1972). The valuation of option contracts and a test of market efficiency. The journal of finance, 27(2), 399-417.

Indexed at, Google Scholar, Cross Ref

Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of political economy, 81(3), 637-654.

Indexed at, Google Scholar, Cross Ref

Boness, A.J. (1964). Elements of a theory of stock-option value. Journal of Political Economy, 72(2), 163-175.

Google Scholar, Cross Ref

Bonz, C., Angeli, A. (2010). Changes in the creditability of the Black-Scholes option pricing model due to financial turbulences.

Indexed at, Google Scholar

Boyack, K.W., & Klavans, R. (2010). Co‐citation analysis, bibliographic coupling, and direct citation: Which citation approach represents the research front most accurately?. Journal of the American Society for information Science and Technology, 61(12), 2389-2404.

Google Scholar, Cross Ref

Bulan, L.T. (2005). Real options, irreversible investment and firm uncertainty: new evidence from US firms. Review of Financial Economics, 14(3-4), 255-279.

Indexed at, Google Scholar, Cross Ref

Carmona, R., Moral, P.D., Hu,P., & Oudjane, N. (2012). An introduction to particle methods with financial applications. In Numerical methods in finance.

Indexed at, Google Scholar, Cross Ref

Chen, D., Liu, Z., Luo, Z., Webber, M., & Chen, J. (2016). Bibliometric and visualized analysis of emergy research. Ecological Engineering, 90, 285-293.

Indexed at, Google Scholar, Cross Ref

Choi, S., & Wohar, M.E. (1994). S & P 500 index options prices and the Black-Scholes option pricing model. Applied Financial Economics, 4(4), 249-263.

Google Scholar, Cross Ref

Christoffersen, P., & Jacobs, K. (2001). The Importance of the Loss Function in Option Pricing. Journal of Financial Economics. 72.

Google Scholar

Cox, J.C., & Ross, S.A. (1976). The valuation of options for alternative stochastic processes. Journal of financial economics, 3(1-2), 145-166.       

Google Scholar, Cross Ref

Cox, J.C., Ingersoll, J.E. and Ross, S.A. (1985). A Theory of the Term Structure of Interest Rates. The Econometric Society,53, 385-407.

Indexed at, Google Scholar, Cross Ref

Donthu, N., Kumar, S., Mukherjee, D., Pandey, N., & Lim, W.M. (2021). How to conduct a bibliometric analysis: An overview and guidelines. Journal of Business Research, 133, 285-296.

Indexed at, Google Scholar, Cross Ref

Donthu, N., Kumar, S., Pandey, N., Pandey, N., & Mishra, A. (2021). Mapping the electronic word-of-mouth (eWOM) research: A systematic review and bibliometric analysis. Journal of Business Research, 135, 758-773.

Indexed at, Google Scholar, Cross Ref

Donthu, N., Kumar, S., Pattnaik, D., & Campagna, C. (2020). Journal of marketing theory and practice: a retrospective of 2005–2019. Journal of Marketing Theory and Practice, 28(2), 117-137.

Indexed at, Google Scholar, Cross Ref

Donthu, N., Kumar, S., Pattnaik, D., & Lim, W.M. (2021). A bibliometric retrospection of marketing from the lens of psychology: Insights from Psychology & Marketing. Psychology & Marketing, 38(5), 834-865.

Google Scholar, Cross Ref

Eduardsen, J., & Marinova, S. (2020). Internationalisation and risk: Literature review, integrative framework and research agenda. International Business Review, 29(3), 101688.

Indexed at, Google Scholar, Cross Ref

Fonseca, B.d., Sampaio, R.B., Fonseca, M.V.d. et al. (2016). Co-authorship network analysis in health research: method and potential use. Health research policy and systems, 14(1), 1-10.

Indexed at, Google Scholar, Cross Ref

Frino, A., Lodh, S. C., & Khan, E. (2019). The black scholes call option pricing model and the Australian options market: Where are we after 15 years. The International Journal of Accounting and Business Society, 1(1), 40-57.

Indexed at, Google Scholar

Gençay, R., & Salih, A. (2003). Degree of mispricing with the Black-Scholes model and nonparametric cures. Economics and Finance. Annals, 4, 73-101.

Indexed at, Google Scholar

Heston, S. L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The review of financial studies, 6(2), 327-343.

Indexed at, Google Scholar, Cross Ref

Hull, J., & White, A. (1987). The pricing of options on assets with stochastic volatilities. The journal of Finance, 42(2), 281-300.

Indexed at, Google Scholar, Cross Ref

Khan, M. U., Gupta, A., & Siraj, S. (2013). Empirical testing of modified Black-Scholes option pricing model formula on NSE derivative market in India. International Journal of Economics and Financial Issues, 3(1), 87-98.

Indexed at, Google Scholar

Kim, H., Rhim, J. C., & Khayum, M. F. (1997). An empirical investigation of put option pricing: a specification test of at-the-money option implied volatility. Journal of Financial and Strategic Decisions, 10(2).

Google Scholar

Kumar, R., & Agrawal, R. (2017). An empirical investigation of the Black-Scholes call option pricing model with reference to NSE. International Journal of BRIC Business Research (IJBBR), 6(2), 1-11.

Google Scholar, Cross Ref

Kumar, S., Sureka, R., & Colombage, S. (2020). Capital structure of SMEs: a systematic literature review and bibliometric analysis. Management Review Quarterly, 70(4), 535-565.

Indexed at, Google Scholar

Kumar, S., Marrone, M., Liu, Q., & Pandey, N. (2020). Twenty years of the International Journal of Accounting Information Systems: A bibliometric analysis. International Journal of Accounting Information Systems, 39, 100488.

Indexed at, Google Scholar, Cross Ref

Kumar, S., Lim, W.M., Pandey, N., & Christopher Westland, J. (2021). 20 years of electronic commerce research. Electronic Commerce Research, 21(1), 1-40.

Indexed at, Google Scholar

Kumar, S., Pandey, N., Burton, B., & Sureka, R. (2021). Research patterns and intellectual structure of Managerial Auditing Journal: a retrospective using bibliometric analysis during 1986-2019. Managerial Auditing Journal.

Indexed at, Google Scholar, Cross Ref

Kumar, S., Pandey, N., Lim, W.M., Chatterjee, A.N., & Pandey, N. (2021). What do we know about transfer pricing? Insights from bibliometric analysis. Journal of Business Research, 134, 275-287.

Google Scholar, Cross Ref

Kumar, S., Pandey, N., & Mukherjee, D. (2022). Cross Cultural and Strategic Management: a retrospective overview using bibliometric analysis. Cross Cultural & Strategic Management.

Indexed at, Cross Ref

MacBeth, J.D., & Merville, L.J. (1980). Tests of the Black-Scholes and Cox call option valuation models. The Journal of Finance, 35(2), 285-301.

Indexed at, Google Scholar, Cross Ref

Madan, D.B., & Schoutens, W. (2017). Conic option pricing. The Journal of Derivatives, 25(1), 10-36.

Indexed at, Google Scholar, Cross Ref

Makhudu, T. (2011). Real options and property development decision making. Real Estate Finance, 27(5), 5-16.

Google Scholar

Mallawaarachchi, H., Sandanayake, Y., Karunasena, G., & Liu, C. (2020). Unveiling the conceptual development of industrial symbiosis: Bibliometric analysis. Journal of cleaner production, 258, 120618.

Indexed at, Google Scholar, Cross Ref

McKenzie, G. D., Subedar, Z. (2017). An empirical investigation of the Black-Scholes model: evidence from the Australian Stock Exchange. Australasian Accounting, Business and Finance Journal, 1(4), 71-82.

Indexed at, Google Scholar, Cross Ref

Merton, R.C. (1973). The relationship between put and call option prices: Comment. Journal of Finance, 28(1), 183-184.

Indexed at, Google Scholar

Merton, R.C. (1973). Theory of rational option pricing. The Bell Journal of economics and management science, 141-183.

Indexed at, Google Scholar, Cross Ref

Merton, R.C. (1973). An intertemporal capital asset pricing model. Econometrica: Journal of the Econometric Society, 867-887.

Indexed at, Google Scholar, Cross Ref

Merton, R.C. (1976). Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics, 3(1-2), 125-144.

Google Scholar, Cross Ref

Mishra, S. K. (2012). Pricing of index options using Black’s Scholes model. Global Journal of Management and Business Research, 12(3), 89–96.

Moher, D., Liberati, A., Tetzlaff, J., Altman, D.G., & PRISMA Group*. (2009). Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Annals of internal medicine, 151(4), 264-269.

Indexed at, Google Scholar, Cross Ref

Mukherjee, D., Kumar, S., Donthu, N., & Pandey, N. (2021). Research published in management international review from 2006 to 2020: A bibliometric analysis and future directions. Management International Review, 1-44.

Indexed at, Google Scholar, Cross Ref

Mukherjee, D., Kumar, S., Mukherjee, D., & Goyal, K. (2022). Mapping five decades of international business and management research on India: A bibliometric analysis and future directions. Journal of Business Research, 145, 864-891.

Indexed at, Google Scholar, Cross Ref

Nilakantan, N. S., Sethi, T. (2012). Applicability of Black-Scholes model in Indian capital markets. In JBIMS Research Conference.

Google Scholar

Panduranga, V. (2013). Relevance of Black-Scholes option pricing model in indian derivatives markets–a study of cement stock options. International Journal of Multidisciplinary Research in Social and Management Sciences, 1(4), 91-95.

Google Scholar

Perianes-Rodriguez, A., Waltman, L., & Van Eck, N.J. (2016). Constructing bibliometric networks: A comparison between full and fractional counting. Journal of informetrics, 10(4), 1178-1195.

Indexed at, Google Scholar, Cross Ref

Persson, O. (2010). Identifying research themes with weighted direct citation links. Journal of Informetrics, 4(3), 415-422.

Indexed at, Google Scholar, Cross Ref

Petticrew, M., & Roberts, H. (2008). Systematic reviews in the social sciences: A practical guide.

Indexed at, Google Scholar

Pittway, L. (2008). Systematic literature reviews. In: Thorpe R, Holt R The SAGE dictionary of qualitative management research. London: SAGE Publications.

Rajanikanth, C., & Reddy, E. L. (2015). Analysis of price using Black Scholes and Greek letters in derivative European option market. International Journal of Research in Management, Science & Technology, 3(1), 34-37.   

Google Scholar

Ray, S. (2012). A close look into Black-Scholes option pricing model. Journal of Science, 2(4), 172-178.

Indexed at, Google Scholar

Razera, A.L., Errera, M.R., Dos Santos, E.D., Isoldi, L.A., & Rocha, L.A.O. (2018). Constructal network of scientific publications, CO-authorship and citations. Proc Roman Acad Ser A-Math Phys Tech Sci Inform Sci, 18, 105–110

Indexed at, Google Scholar

Ren, R., Hu,W., Dong, J., Sun, B., Chen, Y., & Chen, Z. (2019). A systematic literature review of green and sustainable logistics: bibliometric analysis, research trend and knowledge taxonomy. International journal of environmental research and public health, 17(1), 261.

Indexed at, Google Scholar

Rodrigo, M.R., & Mamon, R.S. (2006). An alternative approach to solving the Black–Scholes equation with time-varying parameters. Applied Mathematics Letters, 19(4), 398-402.

Indexed at, Google Scholar, Cross Ref

Saade, S. (2015). Investor sentiment and the underperformance of technology firms initial public offerings. Research in International Business and Finance, 34, 205-232.

Google Scholar, Cross Ref

Scott, L.O. (1987). Option pricing when the variance changes randomly: Theory, estimation, and an application. Journal of Financial and Quantitative analysis, 22(4), 419-438.

Indexed at, Google Scholar

Sethi, A., & Nilakantan, N. (2016). Applicability of Black-Scholes model in Indian capital markets. In JBIMS Research Conference.

Google Scholar

Sharma, M., Arora, K. (2015). Study of option price deviation using Black Scholes option pricing model for equity options in India. International Journal of Research in Commerce, Economics & Management, 5(10), 18-23.

Google Scholar

Singh, S., & Walia, N. (2020). Momentum investing: a systematic literature review and bibliometric analysis. Management Review Quarterly, 1-27.

Indexed at, Google Scholar

Smith Jr, C.W. (1976). Option pricing: A review. Journal of Financial Economics, 3(1-2), 3-51.

Google Scholar, Cross Ref

Srijanani, D., & Vijaya, T. (2018). A study on impact of gender in investment decisions. Journal of Management Research and Analysis, 5(2), 161-165.

Google Scholar

Srivastava, A., & Shastri, M. (2018). A study of relevance of Black-Scholes model on option prices of Indian stock market. International Journal of Governance and Financial Intermediation, 1(1), 82-104.

Indexed at, Google Scholar

Stein, E.M., & Stein, J.C. (1991). Stock price distributions with stochastic volatility: an analytic approach. The review of financial studies, 4(4), 727-752.

Indexed at, Google Scholar, Cross Ref

Surwase, G., Sagar, A., Kademani, B.S., & Bhanumurthy, K. (2011). Co-citation analysis: an overview.

Google Scholar

Ter Huurne, M., Ronteltap, A., Corten, R., & Buskens, V. (2017). Antecedents of trust in the sharing economy: A systematic review. Journal of Consumer Behaviour, 16(6), 485-498.

Indexed at, Google Scholar, Cross Ref

Torraco, R.J. (2005). Writing integrative literature reviews: Guidelines and examples. Human resource development review, 4(3), 356-367.

Indexed at, Google Scholar, Cross Ref

Tripathi, V., & Gupta, S. (2010). Effectiveness of the Skewness and Kurtosis adjusted Black-Scholes model in pricing Nifty call options.

Indexed at, Google Scholar, Cross Ref

Trujillo, C. M., & Long, T. M. (2018). Document co-citation analysis to enhance transdisciplinary research. Science advances, 4(1), e1701130.

Indexed at, Google Scholar, Cross Ref

Van Oorschot, J. A., Hofman, E., & Halman, J. I. (2018). A bibliometric review of the innovation adoption literature. Technological Forecasting and Social Change, 134, 1-21.

Indexed at, Google Scholar, Cross Ref

Viglia, G., Kumar, S., Pandey, N., & Joshi, Y. (2022). Forty years of The Service Industries Journal: a bibliometric review. The service industries journal, 42(1-2), 1-20.

Indexed at, Google Scholar, Cross Ref

Zheng, Y. (2015). The linkage between aggregate investor sentiment and metal futures returns: A nonlinear approach. The Quarterly Review of Economics and Finance, 58, 128-142.

Indexed at, Google Scholar, Cross Ref

Zumbach, G. (2012). Option pricing and ARCH processes. Finance Research Letters, 9(3), 144-156.

Indexed at, Google Scholar, Cross Ref

Received: 12-Sep-2022, Manuscript No. AAFSJ-22-12543; Editor assigned: 14-Sep-2022, PreQC No. AAFSJ-22-12543(PQ); Reviewed: 28-Sep-2022, QC No. AAFSJ-22-12543; Revised: 21-Nov-2022, Manuscript No. AAFSJ-22-12543(R); Published: 28-Nov-2022