Introduction

Mathematics is the root of many different areas. It provides the foundations for many different areas, including Statistics, Engineering, Economics, and Finance. Many theories in Mathematics can be used in many applications, including solving problems in our daily lives in reality. The theory of derivative plays a tremendously crucial role in teaching Mathematics and addressing many different mathematical issues and issues from many different areas. Hence, many scientists and educators have been studying the theory of the derivative of functions with its applications. For example, Wengert (1964) introduced a simple automatic derivative evaluation program. Osler (1970) provided the fractional derivative of a composite function. Janin (1984) presented the directional derivative of the marginal function in nonlinear programming. Correa & Seeger (1985) developed the directional derivative of a minimax function. Cardaliaguet & Euvrard (1992) proposed the approximation of a function and its derivative with a neural network.

In recent years, this issue has continued to be strongly researched and developed. Readers may refer to Lahiri & Sarkar (2004) researched the uniqueness of a meromorphic function and its derivative. Janteng, et al., (2006) studied the coefficient inequality for a function whose derivative has a positive real part. Almeida (2017) offered a Caputo fractional derivative of a function with respect to another function. Almeida, et al., (2018) discussed the fractional differential equations with a Caputo derivative with respect to a kernel function and their applications. Pho, et al., (2020) presented the numerical study of nonlinear 2D optimal control problems with multi-term variable-order fractional derivatives in the Atangana-Baleanu-Caputo sense.

The derivatives of the functions are useful in many scientific areas. Studying the theory of derivative is helpful to academics and students to address issues in Finance, Economics, Engineering, Decision Sciences, and many other areas. In this regards, readers may refer in Fu, et al., (2020); Mahmoudi, et al., (2020); Maleki, et al., (2020a,b); Jalali, et al., (2020); Li, et al., (2020); Suu, et al., (2020); Wang, et al., (2020); Yadav, et al., (2020) for more information.

In education, in recent years, according to the new trend in the National High School Exam in Vietnam for Mathematics, the number of practical Mathematics questions has been increasing. This trend creates certain difficulties for High School students when they take the Mathematics test, including quite good students. Because most teachers and high school students are used to solving theoretical problems, they have less experience putting the theory into practice.

To solve the practical problems well, students have to know Mathematics and other subjects. In addition, students have to know how to use Mathematics to solve practical problems. Nevertheless, to our knowledge, in the current textbook curriculum, the number of practical exercises is still very limited. Moreover, the number of practical questions using knowledge of “The theory of Derivative” is very important in many examinations in Vietnam.

Teaching mathematics in a practical manner to achieve the best results is a practical and urgent topic and research direction in the current context of educational innovation. Teaching in this direction helps students to develop their ability to solve their problems in life. It is also suitable for the current national development and the development of science and technology of the Fourth Industrial Revolution in Vietnam and other countries.

The Theory of Derivative plays a very important and significant role in many sciences. The Theory of Derivative has been taught at all levels in any high school and at the university for all students, including students majoring in Mathematics and not majoring in Mathematics. In addition, the Theory of Derivative is an effective supporting tool for any specialized Science in the field of Finance, Economics, and others. Therefore, effective teaching of the Theory of Derivative to students is extremely important and can improve education quality. Meanwhile, as we know, teaching and learning about the Theory of Derivative have many limitations that need to be studied to have solutions to improve the quality of vocational training for students.

Therefore, it is extremely meaningful to have a research paper about the applications of the Theory of Derivative in Decision Sciences, Education, and many other areas. In this paper, we first present the Theory of Derivative systematically in detail. We then introduce the Theory of Derivative in Decision Sciences, Education, and other areas. This paper is organized as follows. We present the definitions and some important properties of the Theory of Derivative in Section 2. Applications of the derivative of the functions in Decision Sciences, Education, and others are discussed in Sections 3, 4 and 5. Finally, some concluding remarks are given in the last section.

Theory of Derivative

Theory of Derivative Definition of the Derivative of the Function at a Point

Let y=f(x)be a function defined on the (a,b) interval and 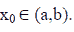If there exists the finite limitation of 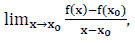then the limitation is called the derivative of the function 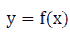at a point x₀ denoted by .

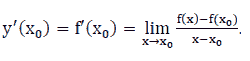Let .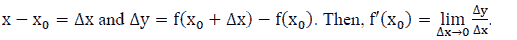

We note that 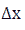is called the argument increment at 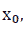and 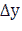is called the corresponding increment of the function. We also note that if the function has a derivative in the (a, b) interval, then it is continuous on the (a, b) interval.

The Rule of Derivative Calculation by Definition

To calculate the derivative, it is necessary to go through the following three steps:

Step 1: let 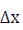be the increment of the argument at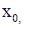

Step 2: set the ratio 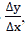and

Step 3: calculate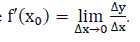

The Rules of Derivatives

Let 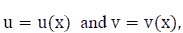then we have:

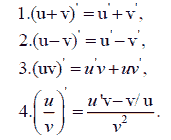
The Geometrical Meaning of the Derivative

If there exists 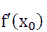and the slope of the tangent of the graph of the function 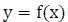at point 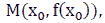then the tangent equation of the function graph 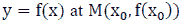has the following form: .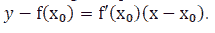

The Physical Meaning of the Derivative

We Give the Following Example to Show the Physical Meaning of the Derivative:

Example: If 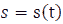is the movement at time t, then 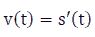is the instantaneous velocity of the movement 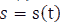at time t.

Definition of the Maximum and Minimum Values

Given a function 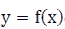defined in the K (open, close, half-open, and half-close) interval, we will discuss the maximum and minimum values in the following subsections.

The Maximum Value

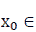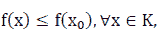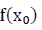If there exists K such that then is called the maximum value of f ( x) on the K, denoted by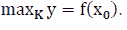

The Minimum Value

If there exists 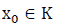such that 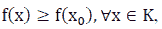then 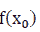is called the maximum value of f (x) on the K, denoted by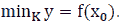

The Procedure to find the Maximum and Minimum Values

Problem 1: Consider the (a, b) Interval

For this problem, we only make a table of different functions. Based on the table, we can easily conclude that the maximum and minimum values of the function on the (a, b) interval.

Problem 2: Consider the [a, b] Interval

For this problem, one can use the approach discussed in Problem 1 to solve the problem. However, usually, the process contains the following four steps:

Step 1: Calculate the derivative of the function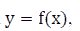

Step 2: find 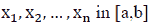such that 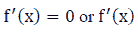is undefined,

Step 3: compute 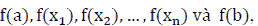and

Step 4: in the values obtained in Step 3, we need to find the largest M and the smallest m such that

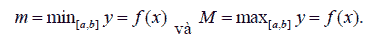
Note 2: If 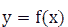is a continuous function on the [a, b] interval, then 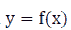has the maximum and minimum values on the [a, b] interval.

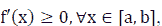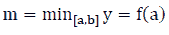Note 3: If then and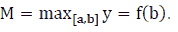

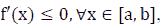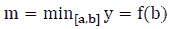Note 4: If then and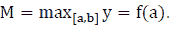

Applications of the Theory of Derivative in Decision Sciences

There are many applications of using the theory of the derivative in Decision Sciences, especially in Applied Mathematics, Statistics, Chemistry, Physics, Economics, and Finance, because the theory of derivative is not only the foundation of Mathematics and Statistics but also the foundation of all areas related to Sciences. This section will present some applications of the theory of derivative in some primary fields, including Applied Mathematics, Statistics, Chemistry, Physics, Economics, and Finance.

The “rate of change” of the quantity of the derivative becomes an extremely important tool. Whenever and wherever change occurs, we will know how it changes by derivative. Specifically, if the function is increasing, the derivative will be positive. The faster it increases, the bigger the derivative. Conversely, the function decreases, the more the derivative will be negative, and the faster the function will decrease.

From a practical perspective, economists could be interested in knowing the economic growth rate to make better decisions in investment. Strategic planners could be interested in getting information about population growth rates in different cities/countries. Chemists could be interested in knowing the chemical reaction rate, and engineers could calculate the speed and the acceleration of motion. Derivation could be used to solve all these problems. We first present the applications of the derivative of functions to Applied Mathematics.

Applied Mathematics

Derivative also has other good applications in Applied Mathematics. One of them is to find out where the function will reach maximum or minimum values, thereby optimizing various activities in life. When a function increases (positive derivative) and turns to decrease (negative derivative), it passes through the position at which the function reaches its maximum value, and this position is also where its derivative could be 0 (there may have exceptions). A similar argument can be obtained for cases where the function reaches the minimum value.

Using this approach to find the position where the derivative is zero, one can know where a quantity will reach its maximum or minimum value to get the optimized value. Egozcue, et al., (2009, 2010, 2011, 2011a, 2013) use this approach to develop some properties for covariance inequalities, Alghalith & Wong (2020b) use the theory of derivative to extend Stein’s Lemmas to general functions and distributions, Grüss & Chebyshev inequality, and copulas. Engineers will know how to design a can of milk or a can of soda, with the amount of material available, to have a milk carton that holds the most milk.

Specifically, we need a function that describes profit by using product quantity or a function that describes the volume of milk cartons according to the design size. The derivative will help us find out the positions in which the functions are at their greatest value; that is, the optimal choice for manufacturers. In addition, one of the most important uses for a derivative is to indicate the rate of change of a function. Readers may refer to Bandeira, et al., (2012), who introduced the computation of low-degree polynomials and their applications to derivative-free optimization. On the other hand, Pellegrini, et al., (2014) introduced the applications of derivative-free multi-objective algorithms to robust design optimization of a high-speed catamaran in the real ocean environment, Ninomiya & Victoir (2008) introduced the weak approximation of stochastic differential equations with applications to derivative pricing, and Tianhe, et al., (2020) introduced the numerically functional optimization by using the conditionalized PSO algorithm, and others.

Statistics

Both distribution functions and transformations in Statistics often use derivatives and integrals. For example, Pho, et al., (2019a) review the moment generating function, expectation, and variance of ubiquitous distributions with applications in decision sciences. Pho, et al., (2019c) review the optimal solution techniques in decision sciences. The above studies use the derivative and integral theory to address it. In addition, Atangana, et al., (2017) offered a new derivative with a normal distribution kernel and applications. Bai, et al., (2010, 2011a, 2018) use this approach to obtain the multivariate nonlinear causality test. Bai, et al., (2011b, 2012, 2013); Guo, et al., (2018, 2019); Leung & Wong (2008); Niu, et al., (2017, 2018); Wong, et al., (2012) use this approach to obtain different tests for different risk measures. Bai, et al., (2011, 2015, 2020); Ng, et al., (2017) use this approach to obtain stochastic dominance tests. Bai, et al., (2009, 2011); Li, et al., (2018); Leung, et al., (2012); Ng, et al., (2017) use this approach to obtain Markowitz mean-variance optimization. Wong & Bian (2000); Bian, et al., (2013) use the theory of derivative to develop robust Bayesian models, Tiku, et al., (1999 a,b 2000); Wong & Bian (2005) use the theory of derivative to develop a modified MML estimation for regression and time series models. Wong & Miller (1990) use the derivative theory to develop a new ARIMA process with a noise component. Bian, Mc-Aleer & Wong (2011) use the derivative theory to develop the trinomial test. Valenzuela, Wong & Zhu (2020); Chow, Valenzuela & Wong (2021) use the derivative theory to develop a new income distribution index. Guo, et al., (2018) use the derivative theory to develop two statistics to test for the production frontier functions. Leung & Wong (2008a) use the theory of derivative to develop a new profile model. Lam, et al., (2006) use the derivative theory to develop several statistics to test for the random walk model. Tiku & Wong (1998) use the theory of derivative to develop a unit root statistic, Penm, et al., (2003) use the theory of derivative to develop a model for Granger causality and non-causality estimation (Chow et al., 2018, 2018a, 2019; Cheng et al., 2019; Demirer et al., 2019; Gupta et al., 2019), Bai, et al., (2010, 2011, 2018) use the theory of derivative to develop nonlinear Granger causality statistics, and Hui, et al., (2017) use the theory of derivative to develop a nonlinearity statistic.

Chemistry

The derivative has many interesting applications in Chemistry. Specifically, a chemist wants to determine the speed of certain chemical reactions. For example, Argyros, et al., (2016). Introduced the local convergence and a chemical application of derivative-free root-finding methods with one parameter based on interpolation, Echeverria Ciaurri, et al., (2011) presented some derivative-free methodologies generally constrained oil production optimization problems. Murthy & Manthiram (2012) provided some applications of derivative voltammetry in the analysis of the methanol oxidation reaction. In addition, Pho, et al., (2020) presented the soil carbon pool changes in the semi-arid land planting programs.

Physics

The derivative has many important applications in Physics. For instance, a physicist needs to calculate the velocity to find out the acceleration of motion. Weinstock (1974) offered the calculus of variations with applications to physics and engineering, Hilfer (2000) presented the applications of fractional calculus in physics. In addition, Zeidler (2012) provided the applied functional analysis with applications to mathematical physics.

Economics

The derivative has many important applications in economics. For example, economists are interested in estimate an economic growth rate to make the right decisions in investment or forecasts, Campbell (1980) presented the demand for life insurance with applications in economics with uncertainty, Atici, et al., (2006) provided an application of time scales to economics, Córdova-Lepe (2006) introduced the multiplicative derivative as a measure of elasticity in economics, and Scalas (2006) offered the application of continuous-time random walks in finance and economics. Using this derivative feature, companies can calculate the number of products to produce to achieve the highest profit. In addition, Egozcue, Guo & Wong (2015); Guo, Wong, Xu & Zhu (2015); Guo & Wong (2019); Guo, Egozcue & Wong (2020) use this approach to find out the optimal production for regret-averse firms. Guo, Li, Mc-Aleer & Wong (2018) use this approach to obtain the production frontier functions. Wong & Chan (2004) use this approach to obtain the cost of capital for a company. Guo, et al., (2013, 2014, 2016, 2017, 2017a); Guo & Wong (2016); Lam, et al., (2010, 2012); Li & Wong (1999); Wong (2007); Wong & Chan (2008); Wong & Li (1999); Wong & Ma (2008); Wong, et al., (2018) use this approach to examine the behavior of different investors. Sethi, Wong & Acharya (2018) use the derivative theory to develop an economic indicator to examine the sectorial impact of disinflationary monetary policy for different countries.

After using the theory of derivative to develop cointegration and causality, academics and practitioners can use estimation and statistics to study many interesting issues in Economics, see, for example, Cheng, et al., (2013); Chow, et al., (2018a); Chu, et al., (2020); Lv, et al., (2019); Manzur, et al., (1999); Owyong, et al., (2015); Qiao, et al., (2009, 2008b); Woo, et al., (2012). After using the theory of derivative to develop risk measures statistics and stochastic dominance tests, academics and practitioners can use the estimation and statistics to study many interesting issues in Economics, see, for example, Broll, et al., (2006, 2015); Chan, et al., (2012, 2020); Qiao & Wong (2015); Tsang, et al., (2016); Ma & Wong (2010, 2021).

Finance

The derivative has many important applications in finance. For example, Ly, et al., (2019a, b) presented the determining distribution for the products and quotients of dependent and independent random variables by using copulas. They used the derivative and integral theory to address it. Lieberman & Phillips (2017) discussed a multivariate stochastic unit root model to apply derivative pricing. Suu, et al., (2020) presented the net interest margin of commercial banks in Vietnam and among others. Wong & Li (1999); Li & Wong (1999); Wong (2007); Guo & Wong (2016); Egozcue & Wong (2010); Hoang, Wong & Zhu (2015); Bouri, et al., (2018); Lu, et al., (2018) use this approach to obtain diversification solutions and Lu, et al., (2020) use this approach to compare the performance of the lump-sum investing strategy and dollar-cost averaging strategy. Mc-Aleer, Suen & Wong (2016) use the derivative theory to develop some new financial indicators that can be used to trade stocks/funds. Lean, et al., (2015); Vieito, et al., (2015); Zhu, et al., (2019); Hassan, et al., (2020) use the theory of Derivative to measure Financial Crises. Chan, et al., (2014) use the theory of derivative to develop some rules in technical analysis that can be used to generate significant profit in the stock trading, Batmunkh, et al., (2018, 2020) and use the theory of derivative to examine whether there is any Herding Behaviour in the markets, and Lu, et al., (2020) use the theory of derivative to compare different investing strategies. In addition, Alghalith & Wong (2020a) use the theory of derivative to develop the theory of hedging behavior, Hesami, et al., (2020) use the theory of derivative to study the impact of oil price fluctuations for tourism receipts, and Le & Wong (2019) use the theory of derivative to examine the factors that affect a firm’s capital structure decision.

After using the theory of derivative to develop cointegration and causality, academics and practitioners can use the estimation and statistics study many interesting issues in finance, see, for example, Cheng, et al., (2019); Chen, et al., (2008); Chow, et al., (2019); Demirer, et al., (2019); Qiao, et al., (2008, 2018a, 2011); Zhu, et al., (2019). After using the theory of derivative to develop risk measures statistics and stochastic dominance tests, academics and practitioners can use the estimation and statistics study many interesting issues in finance, see, for example, Clark, et al., (2016); Egozcue, et al., (2011); Egozcue & Wong (2010); Fong, et al., (2008, 2005); Gasbarro, et al., (2012, 2007); Hoang, et al., (2018, 2015, 2015a, 2019); Lean, et al., (2015, 2010, 2012, 2007); Lozza, et al., (2018); Qiao, et al., (2012, 2010, 2013); Wong, et al., (2018, 2008); Lo, et al., (2021); Nguyen, et al., (2019b, 2020b); Pho, et al., (2021); Plakandaras, et al., (2019); Vieito, et al., (2020); Yousaf, et al., (2020). In addition, readers may refer in Salamzadeh, et al., (2013); Allen (2017); Doshmanli, et al., (2018); Tajpour & Salamzadeh (2019); Salamzadeh (2020) for more information.

Applications of the Theory of Derivative in Education

Development oriented education program in capacity gets attention since 1990. It becomes one of the most important international education trends. Project-based learning with a flipped classroom model in B-learning has been proven to be effective in Vietnam and many other countries. This is an approach to help students to improve their capacity in applying their knowledge to solve practical problems. The goal of the method is to form and develop learners’ competencies. It requires learners to apply their knowledge of skills effectively and appropriately in any complex situation in learning in school and out of school in real life with confidence. Since then, it has also met the requirements of the Fourth Industrial Revolution.

The approach helps learners to getting knowledge in lectures, and to improving the capacity to solve real-life problems. Therefore, teaching needs to innovate and integrate good scientific knowledge with practical use. Hence, when designing lessons for learners, it is necessary to pay attention and choose the teaching method that is reasonable for integrated teaching. In particular, it is necessary to focus on applying knowledge to practical problems.

In Vietnam, many authors have been studying the issue. For example, Thanh & Dung (2015) presented project-based learning with the flipped classroom model in B-learning. Tung (2015) introduced teaching integrated with subjects in medical statistics, informatics, and scientific research in the Universities of Medicine and Pharmacy. Thanh (2018) developed an educational program that can be used in teaching students in high-level classes and helping them with their problem-solving homework.

Liu, et al., (2017) presented a project-based model with a spiraling curriculum that enables teachers to learn efficiently. Fidalgo-Blanco, et al., (2018) developed a flip teaching model by using knowledge management. Hinojo-Lucena, et al., (2018) developed a strategy in physical education that can be used in the flipped classroom and evaluates university students’ academic performance in school. Sergis, Sampson & Pelliccione (2018) introduced a strategy that can be used in investigating the impact of Flipped Classrooms on students’ learning experiences.

Thanh & Dung (2015) have applied the method in teaching Information Technology (IT). The results show that it not only stimulates learning, enhances student learning outcomes, but also helps them improve their ability to act. In this paper, we discuss their model in detail and complete the process of the method and help university lecturers document the subjects. This method can also be applied to teaching the topic of the Theory of Matrix to university students. Nguyen, et al., (2019a) have applied the method on teaching mathematics by practical decision modeling and Nguyen, et al., (2020a) have applied the method to study depression, anxiety, and social media addiction among undergraduate students.

Application of Project Based Learning with Flipped Classroom Model in B-learning to teach the Topic of Derivative Theories

Derivative Theory Courses

The course has two main objectives as follows: First, students have to memorize and understand most of the formulas related to derivative theory. After that, students learn how to apply the knowledge of matrix theory to solve practical problems.

The Process of Teaching Implementation

Step 1. Rearrange the learning plan of the subject and the learning resources according to the learner's perceptions.

Step 2. Design teaching materials for students' self-study activities at home to prepare for class in the classroom, especially for the following issues: We first build video to be used in lectures. The materials will be given to students so that they can study the theoretical knowledge by themselves at the basic level. We then build projects for groups. Finally, we arrange learning activities that students can learn at home.

Step 3. Design teaching materials for classroom lessons, see the process of organizing teaching material to be used during class in the following sections.

The loop of the above 3 steps is continued throughout the course. To help readers easily approach and apply this method, we present it in detail in the next section.

Integrating Project Teaching and Problem-Solving Teaching

Based on research by Thanh & Dung (2015). We propose the steps of organizing teaching on the basis of integration with project teaching as follows: as shows in Table 1.

Table 1 Steps of Organizing Teaching
Stages	Steps	Teacher Activities	Student Activities
Identify and explore problems	Start and clarify problems	Introduce the problem and	- Work in team
		class organization: grouping, rules on time, assignment, presentation, evaluation.	- Identify words, terms, concepts.
			- Identify known factors and unknown factors.
	Propose ideas and hypotheses.	Teachers require technical and standards.	Based on known and unknown knowledge, students propose ideas and hypotheses to solve problems. Here the ideas have not been verified, there is no solid basis.
	Identify relevant knowledge	In order for students not to deviate from the research, teachers can give necessary suggestions.	From the proposed hypotheses, students determine what content is needed to solve the problem. In addition, students need to list what they need to solve problems, propose new knowledge to research.
Learn related knowledge	Orientation of information source	Suggested sources of information.	- Search for information in textbooks, the internet, or talk to experts.
	Self-study		The knowledge content is broken down into knowledge units suitable for individual or small group self-study.
			Students present results, processes, approaches and principles diagrams, etc.
Problem solving	Systematize knowledge	Hold the discussion.	The report, discuss the research results of the groups.
	Verify the hypothesis		Verify the hypothesis with logical reasoning and valid evidence. In cases where practical explanations cannot be provided, it is necessary to return to the hypothesis proposal.
Conclusion	Show the results	Teacher reviews and comments.	Present in the form of a small report or answer sheet. Students can also report real products or simulation models.

Illustrations

The applications of Derivative Theory in practical problems are diverse and plentiful. The practical applied mathematical problems are oriented towards the exam in Vietnam as well as in the practical world recently. In this section, we illustrate the Theory of Derivative by using some solved detailed examination questions in Vietnam.

Question 1 (National High School Test 2018)

Mr. A plans to use of glass to make a glass aquarium shaped like a capless rectangular box, know that the length is twice the width (The joints have negligible size). How big is the aquarium (the result is rounded to the nearest hundred)? as shows in Figure 1.

It can be observed from Figure 1 that

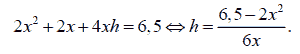
Since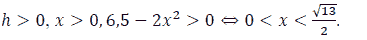

In addition, we have

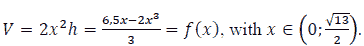Thus,

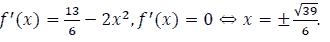
We construct the variation table as follows:

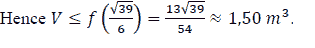
Question 2 (Exam for good students in Hai Duong province, Vietnam 2018-2019)

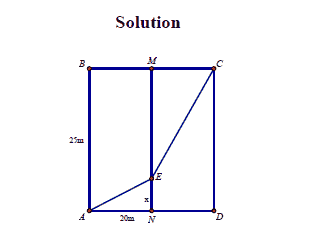
A rectangular plot of land ABCD has length AB=25m, width AD=20m, is divided into two equal parts by the MN barrier (M and N are midpoints of BC and AD, respectively). A construction team makes a road from A to C over the MN crossing, knowing that when making roads in the ABMN domain every 15 m worked and when working in the CDNM every hour can work 30 m. Calculate the shortest time that the construction team can make the path from A to C.

Suppose the path from A to C meets the MN barrier at E.

Let NE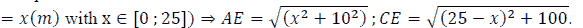

Time to make the road from A to C is calculated by

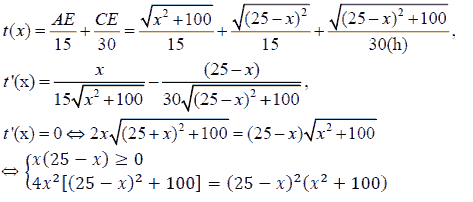
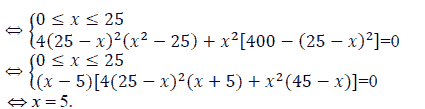
Thus, the time to make the road from A to C is 5 hours.

Question 3 (Exam for good students in Can Tho province, Vietnam 2018-2019)

A high-quality bus from Can Tho to Hanoi can carry up to 50 passengers on a trip. According to the calculation of the garage, if the car can carry k passengers, the price that each customer must pay when traveling this route is 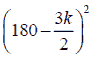hundred VNÐ). Calculate the number of passengers per ride so that the total amount of money collected from passengers the most.

The amount collected on each ride is T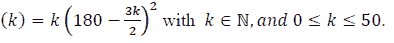

Let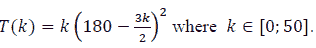

It can be seen that T (k) continuous on [ 0; 50 ]

and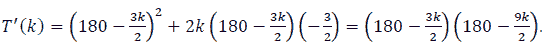

Thus, 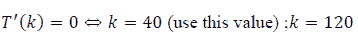(remove this value).

Thereafter, we get: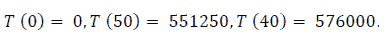

Hence, the maximum value of T (k) is T (40) = 576000, and the maximum amount of fund is collected when a vehicle carries 40 passengers, and the amount is 57600000 VNĐ.

Question 4 (Exam for good students in Quang Ninh province, Vietnam 2018-2019)

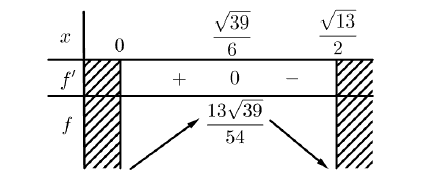
Mr. An's house wants to put a worker in an aquarium, made of transparent glass material, without a rectangular lid with a volume of 400000 cm³ of water. Know that the height of the aquarium is 2 times the width of the aquarium. Determine the bottom area of the aquarium to save the raw materials most. as shows in Figure 4.

Let a , b ,c ( cm ) be the width, length, and height of a rectangular box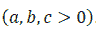

Under the assumption, we have V = abc = 400000 and c = 2a.

Hence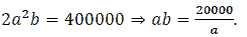

We have the total surrounding area and the bottom area of the aquarium

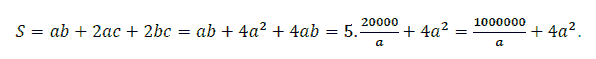
Let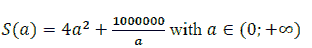

It has been seen that S ( a ) continuous on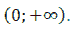

and

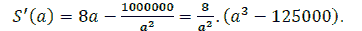
Thus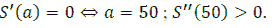

Thereafter we obtain S reaches the minimum value at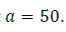

Then the area of the bottom is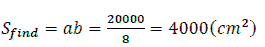

Question 5 (Exam for Good Students in Ha Tinh Province, Vietnam 2018-2019)

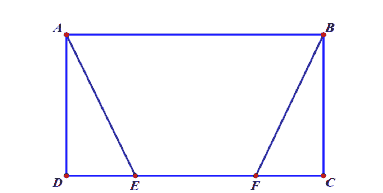
In the desert, there is a rectangular plot of land ABCD of length AB=70 km, width AD=10 km. The average speed of a motorbike on this site is 20 km/h, if going on CD then the speed is 40 km/h. A motorcyclist departs from A at 8 am and wants to go to B after 3 hours. Ask that person can come to B in time? Develop a plan to move on the land from A to B to spend the least time.

Solution

Option 1: To go from A to B if only moving on segment AB, the number of hours is:

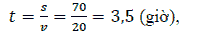
So, in this case, it is not possible to arrive in time B after 3 hours as required math problem.

Because the speed on the land (except for the CD) is 20 km/h, so just follow the AB in no time, all other roads that do not travel on the CD are not timely. Thus we consider Option 2. as shows in Figure 5.

Option 2:

To go from A to B and have to go on the edge of the CD. Suppose going from A to E, from E to

F, and from F to B (as shown in Figure 5). Let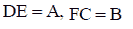

Thus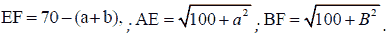

Then, the time to move from A to B is

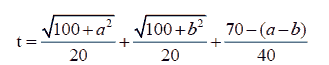
Apply the inequality: 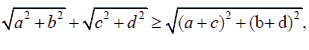we have

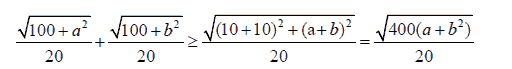
Equality occurs when a=b.

Thereafter we get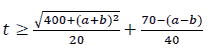

Let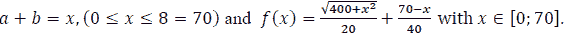

It has been seen that this function is continuous on [ 0 ; 70 ]. We have

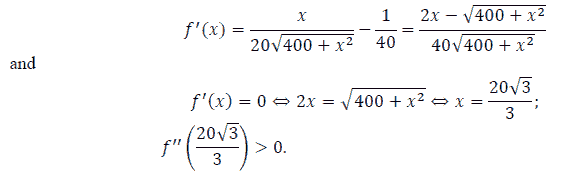
Hence, the minimum value of 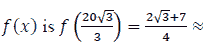1,58 so that the person can get to B in time and as quickly as Option 2.

We note that Figures 1, 2, and 5 are self-drawn using GeoGebra computational software. In the other two images: Figures 3 and 4, we crawl and search the internet.

Conclusion

The derivatives of the functions are useful in many scientific areas. Studying the theory of derivative is helpful to academics and students to address issues in Finance, Economics, Engineering, Decision Sciences, and many other areas. The derivative theory has been widely applied in many areas in Sciences, including Mathematics, Statistics, Engineering, Education, Economics and Finance, etc. On the other hand, Education is one of the most important topics in research in many countries, especially education with practical problems. Thus, Education in Science is a very important piece of research for many countries because it will help in the development and sustainability of every country in the world while the derivative theory is one of the most important areas in Education in Science.

In this paper, we review the derivative theory in Education. We first present the overview of the Derivative Theory. We then discuss how to build up some models in mathematics, finance, economics, and statistics by using the derivative theory and discuss the applications by using the theory of derivative in Decision Sciences and other related areas like Mathematics, Economics, Finance, Statistics, and Education with real-life examples. The extension could apply the derivative theory to many different areas, including exchange rate (Batai et al., 2017; Chen et al., 2011), capital structure (Wong & Chan, 2004; Chang et al., 2019), students’ achievements (Hau et al., 2019, 2020; Tuan et al., 2019), logistics service (Tran et al., 2019; Thipwong et al., 2020b; Moslehpour et al., 2018), and hotel management (Thipwong et al., 2020a; Tang et al., 2014). There are many other areas academics and practitioners can apply the review discussed in our paper, readers may refer to Chang, et al., (2017); Wong (2020) for more information.

Acknowledgment

The fifth author would like to thank Robert B. Miller and Howard E. Thompson for their continuous guidance and encouragement. This research has been supported by Sai Gon University, Hong Duc University, Can Tho University, Asia University, China Medical University Hospital, The Hang Seng University of Hong Kong, Nanyang Technological University, and Ministry of Science and Technology (MOST, Project Numbers 106-2410-H-468-002 and 107-2410-H-468-002-MY3), Taiwan.

References

1. Alghalith, M., & Wong, W.K. (2020a). Welfare gains from macro-hedging. Annals of Financial Economics, 15(2), 2050009.
2. Alghalith, M., & Wong, W.K., (2020b). Extension of stein's lemmas to general functions and distributions. Advances in Decision Sciences, 24(4), 77-88.
3. Allen, D.E. (2017). Practical aspects of R in finance, management information, and decision sciences. Journal of Management Information and Decision Sciences, 20(1).
4. Almeida, R. (2017). A caputo fractional derivative of a function with respect to another function. Communications in Nonlinear Science and Numerical Simulation, 44, 460-481.
5. Almeida, R., Malinowska, A.B., & Monteiro, M.T.T. (2018). Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications. Mathematical Methods in the Applied Sciences, 41(1), 336-352.
6. Argyros, I.K., Magreñán, Á.A., & Orcos, L. (2016). Local convergence and a chemical application of derivative free root finding methods with one parameter based on interpolation. Journal of Mathematical Chemistry, 54(7), 1404-1416.
7. Atangana, A., & Gómez-Aguilar, J.F. (2017). A new derivative with normal distribution kernel: Theory, methods and applications. Physica A: Statistical mechanics and its applications, 476, 1-14.
8. Atici, F.M., Biles, D.C., & Lebedinsky, A. (2006). An application of time scales to economics. Mathematical and Computer Modelling, 43(7-8), 718-726.
9. Bai, Z.D., Hui, Y.C., Wong, W.K., & Zitikis, R. (2012). Prospect performance evaluation: Making a case for a non- asymptotic UMPU test. Journal of Financial Econometrics, 10(4), 703-732.
10. Bai, Z.D., Li, H., Liu, H.X., & Wong, W.K. (2011). Test statistics for prospect and Markowitz stochastic dominances with applications. Econometrics Journal, 122, 1-26.
11. Bai, Z.D., Li, H., McAleer, M., & Wong, W.K. (2015). Stochastic dominance statistics for risk averters and risk seekers: An analysis of stock preferences for USA and China. Quantitative Finance, 15(5), 889-900.
12. Bai, Z.D., Li, H., Wong, W.K., & Zhang, B.Z. (2011a). Multivariate causality tests with simulation and application. Statistics and Probability Letters, 81(8), 1063-1071.
13. Bai, Z.D., Liu, H.X., & Wong, W.K. (2009). Enhancement of the applicability of Markowitz’s portfolio optimization by utilizing random matrix theory. Mathematical Finance, 19(4), 639-667.
14. Bai, Z.D., Liu, H.X., & Wong, W.K. (2011b). Asymptotic properties of eigenmatrices of a large sample covariance matrix. Annals of Applied Probability, 21(5), 1994–2015.
15. Bai, Z.D., Phoon, K.F., Wang, K.Y., & Wong, W.K. (2013). The performance of commodity trading advisors: A mean-variance-ratio test approach. North American Journal of Economics and Finance, 25, 188-201.
16. Bai, Z.D., Wang, K.Y., & Wong, W.K. (2011c). Mean-variance ratio test, a complement to coefficient of variation test and Sharpe ratio test. Statistics and Probability Letters, 81(8), 1078-1085.
17. Bai, Z.D., Wong, W.K., & Zhang, B.Z. (2010). Multivariate linear and non-linear causality tests. Mathematics and Computers in Simulation, 81, 5-17.
18. Bandeira, A.S., Scheinberg, K., & Vicente, L.N. (2012). Computation of sparse low degree interpolating polynomials and their application to derivative-free optimization. Mathematical programming, 134(1), 223-257.
19. Batai, A., Chu, A.M.Y., Lv, Z.H., & Wong, W.K. (2017). China’s impact on mongolian exchange rate. Journal of Management Information and Decision Sciences, 20(1), 1-22.
20. Bian, G., McAleer, M., & Wong, W.K. (2011). A trinomial test for paired data when there are many ties. Mathematics and Computers in Simulation, 81(6), 1153-1160.
21. Bouri, E., Gupta, R., Wong, W.K., & Zhu, Z.Z. (2018). Is wine a good choice for investment? Pacific-Basin Finance Journal, 51, 171-183.
22. Broll, U., Guo, X., Welzel, P., & Wong, W.K. (2015). The banking firm and risk taking in a two-moment decision model. Economic Modelling, 50, 275–280.
23. Broll, U., Wahl, J.E., & Wong, W.K. (2006). Elasticity of risk aversion and international trade. Economics Letters, 91(1), 126-130.
24. Campbell, R.A. (1980). The demand for life insurance: An application of the economics of uncertainty. The Journal of Finance, 35(5), 1155-1172.
25. Cardaliaguet, P., & Euvrard, G. (1992). Approximation of a function and its derivative with a neural network. Neural Networks, 5(2), 207-220.
26. Chan, R.H., Clark, E., Guo, X., & Wong, W.K. (2020). New Development on the third order stochastic dominance for risk-averse and risk-seeking investors with application in risk management. Risk Management, 22, 108-132.
27. Chang, C.C., Batmunkh, M.U., Wong, W.K., & Jargalsaikhan, M. (2019). Relationship between capital structure and profitability: Evidence from four Asian tigers. Journal of Management Information and Decision Sciences, 22(2), 54-65.
28. Chang, C.L., McAleer, M., & Wong, W.K. (2017). Management information, decision sciences, and financial economics: A connection. Journal of Management Information and Decision Sciences, 20, 1-19.
29. Chen, H., Fausten, D.K., & Wong, W.K. (2011). Evolution of the Trans-Atlantic exchange rate before and after the birth of the Euro and policy implications. Applied Economics, 43(16), 1965-1977.
30. Cordova-Lepe, F. (2006). The multiplicative derivative as a measure of elasticity in economics. TMAT Revista Latinoamericana de Ciencias e Ingenieria, 2(3), 1-8.
31. Cheng, Y.S., Wong, W.K., & Woo, C.K. (2013). How much have electricity shortages hampered China’s GDP Growth? Energy Policy, 55, 369–373.
32. Chow, S.C., Valenzuela, M.R., & Wong, W.K. (2021). New tests for richness and poorness: A stochastic dominance analysis of income distributions in Hong Kong. Asia Pacific Journal of Operational Research, forthcoming.
33. Chow, S.C., Vieito, J.P., & Wong, W.K. (2019). Do both demand-following and supply-leading theories hold true in developing countries? Physica A: Statistical Mechanics and its Applications, 513, 536-554.
34. Chu, A.M.Y., Lv, Z.H., Wagner, N., & Wong, W.K. (2020). Linear and nonlinear growth determinants: The case of mongolia and its connection to China. Emerging Markets Review, 43, 100693.
35. Clark, E.A., Qiao, Z., & Wong, W.K. (2016). Theories of risk: Testing investor behaviour on the Taiwan stock and stock index futures markets. Economic Inquiry, 54(2), 907-924.
36. Correa, R., & Seeger, A. (1985). Directional derivative of a minimax function. Nonlinear Analysis: Theory, Methods & Applications, 9(1), 13-22.
37. Doshmanli, M., Salamzadeh, Y., & Salamzadeh, A. (2018). Development of SMEs in an emerging economy: does corporate social responsibility matter? International Journal of Management and Enterprise Development, 17(2), 168-191.
38. Echeverria, C.D., Isebor, O.J., & Durlofsky, L.J. (2011). Application of derivative-free methodologies to generally constrained oil production optimisation problems. International Journal of Mathematical Modelling and Numerical Optimisation, 2(2), 134-161.
39. Egozcue, M., Fuentes, G.F., & Wong, W.K. (2009). On some covariance inequalities for monotonic and non-monotonic functions. Journal of Inequalities in Pure and Applied Mathematics, 10(3), Article 75, 1-7.
40. Egozcue, M., Fuentes G.F., Wong, W.K., & Zitikis, R. (2011). Do investors like to diversify? A study of Markowitz preferences. European Journal of Operational Research, 215(1), 188-193.
41. Egozcue, M., Fuentes García, F., Wong, W.K., & Zitikis, R. (2011a). The covariance sign of transformed random variables with applications to economics and finance. IMA Journal of Management Mathematics, 22(3), 291-300.
42. Egozcue, M., Fuentes García, F., Wong, W.K., & Zitikis, R. (2013). Convex combinations of quadrant dependent copulas. Applied Mathematics Letters, 26(2), 249–251.
43. Egozcue, M., Guo, X., & Wong, W.K. (2015). Optimal output for the regret-averse competitive firm under price uncertainty. Eurasian Economic Review, 5(2), 279-295.
44. Egozcue, M., & Wong, W.K. (2010). Gains from diversification: A majorization and stochastic dominance approach. European Journal of Operational Research, 200(3), 893-900.
45. Esmaeil, J., Rjoub, H., & Wong, W.K. (2020). Do oil price shocks and other factors create bigger impacts on Islamic banks than conventional banks? Energies, 13(12), 3106.
46. Fidalgo-Blanco, A., Sein-Echaluce, M.L., & Garcia-Penalvo, F.J. (2018). Ontological flip teaching: A flip teaching model based on knowledge management. Universal Access in the Information Society, 17(3), 475-489.
47. Fong, W.M., Lean, H.H., & Wong, W.K. (2008). Stochastic dominance and behavior towards risk: The market for internet stocks. Journal of Economic Behavior and Organization, 68(1), 194-208.
48. Fong, W.M., Wong, W.K., & Lean, H.H. (2005). International momentum strategies: A stochastic dominance approach. Journal of Financial Markets, 8, 89-109.
49. Fu, W., Parvin, H., Mahmoudi, M.R., Tuan, B.A., & Pho, K.H. (2020). A linear space adjustment by mapping data into an intermediate space and keeping low level data structures. Journal of Experimental & Theoretical Artificial Intelligence, 1-21.
50. Gasbarro, D., Wong, W.K., & Zumwalt, J.K. (2007). Stochastic dominance analysis of iShares. European Journal of Finance, 13, 89-101.
51. Gasbarro, D., Wong, W.K., & Zumwalt, J.K. (2012). Stochastic dominance and behavior towards risk: The market for iShares. Annals of Financial Economics, 7(1), 1250005-1-20.
52. Guo, X., Chan, R.H., Wong, W.K., & Zhu, L.X. (2019). Mean-Variance, Mean-VaR, Mean-CvaR models for portfolio selection with background risk. Risk Management, 21(2), 73-98.
53. Guo, X., Egozcue, M., & Wong, W.K. (2020), Production theory under price uncertainty for firms with disappointment aversion. International Journal of Production Research, forthcoming.
54. Guo, X., Jiang, X.J., & Wong, W.K. (2017). Stochastic dominance and omega ratio: Measures to examine market efficiency, arbitrage opportunity, and anomaly. Economies, 5(4), 38.
55. Guo, X., Li, G.R., McAleer, M., & Wong, W.K. (2018). Specification testing of production in a stochastic frontier model. Sustainability, 10, 3082.
56. Guo, X., McAleer, M., Wong, W.K., & Zhu, L.X. (2017a). A Bayesian approach to excess volatility, short-term underreaction and long-term overreaction during financial crises. North American Journal of Economics and Finance, 42, 346-358.
57. Guo, X., Niu, C.Z., & Wong, W.K. (2019). Farinelli and tibiletti ratio and stochastic dominance. Risk Management, 21(3), 201-213.
58. Guo, X., Post, T. Wong, W.K., & Zhu, L.X. (2014). Moment conditions for almost stochastic dominance. Economics Letters, 124(2), 163-167.
59. Guo, X., Wagener, A., Wong, W.K., & Zhu, L.X. (2018). The two-moment decision model with additive risks. Risk Management, 20(1), 77-94.
60. Guo, X., & Wong, W.K. (2016). Multivariate stochastic dominance for risk averters and risk seekers. RAIRO - Operations Research, 50(3), 575-586.
61. Guo, X., & Wong, W.K. (2019). Comparison of the production behaviour of regret-averse and purely risk-averse firms. Estudios de Economía, 46(2), 157-161.
62. Guo, X., Wong, W.K., Xu, Q.F., & Zhu, L.X. (2015). Production and hedging decisions under regret aversion. Economic Modelling, 51, 153-158.
63. Guo, X., Wong, W.K., & Zhu, L.X. (2016). Almost stochastic dominance for risk averters and risk seekers. Finance Research Letters, 19, 15–21.
64. Guo, X., Zhu, X.H., Wong, W.K., & Zhu, L.X. (2013). A note on almost stochastic dominance. Economics Letters, 121(2), 252-256.
65. Hassan, K., Hoque, A., Gasbarro, D., & Wong, W.K. (2020). Are Islamic stocks immune from financial crises? Evidence from contagion tests. International Review of Economics and Finance, forthcoming.
66. Hau, N.H., Tuan, B.A., Giang, T.T., & Wong, W.K. (2020). Application of assessment in decision sciences: A study on the assessment of students’ mathematical achievement in Vietnam high schools. Journal of Management Information and Decision Sciences, 23(2), 86-111.
67. Hau, N.H., Tuan, B.A., Thao, T.T.T., & Wong, W.K. (2019). Teaching mathematics by practical decision modeling in Vietnam high schools to serve the fourth industrial revolution. Journal of Management Information and Decision Sciences, 22(4), 444-461.
68. Hesami, S., Rustamov, B., Rjoub, H., & Wong, W.K. (2020). Implications of oil price fluctuations for tourism receipts: The case of oil exporting countries. Energies, 13(17), 4349.
69. Hilfer, R. (Ed.). (2000). Applications of fractional calculus in physics. Singapore: World scientific, 35(12), 87-130.
70. Hinojo-Lucena, F.J., Mingorance-Estrada, A.C., Trujillo-Torres, J.M., Aznar-Diaz, I., & Caceres, R.M.P. (2018). Incidence of the flipped classroom in the physical education students’ academic performance in university contexts. Sustainability, 10(5), 1334.
71. Hoang, T.H.V., Lean, H.H., & Wong, W.K. (2015). Is gold good for portfolio diversification? A stochastic dominance analysis of the Paris stock exchange. International Review of Financial Analysis, 42, 98-108.
72. Hoang, V.T.H., Wong, W.K., & Zhu, Z.Z. (2015a). Is gold different for risk-averse and risk-seeking investors? An empirical analysis of the shanghai gold exchange. Economic Modelling, 50, 200-211.
73. Hoang, V.T.H., Zhu, Z.Z., Khamlichi, A.E., & Wong, W.K. (2019). Does the Shari’ah screening impact the gold-stock nexus? A sectorial analysis. Resources Policy, 61, 617-626.
74. Jalali, S.M.J., Park, H.W., Vanani, I.R., & Pho, K.H. (2020). Research trends on big data domain using text mining algorithms. Digital Scholarship in the Humanities.
75. Janin, R. (1984). Directional derivative of the marginal function in nonlinear programming. In Sensitivity, Stability and Parametric Analysis. Springer, Berlin, Heidelberg. 110-126.
76. Janteng, A., Halim, S.A., & Darus, M. (2006). Coefficient inequality for a function whose derivative has a positive real part. Journal of Inequalities in Pure and Applied Mathematics, 7(2), 1-5.
77. Lahiri, I., & Sarkar, A. (2004). Uniqueness of a meromorphic function and its derivative. Journal of Inequalities in Pure and Applied Mathematics, 5(1), 9.
78. Lam, K., Liu, T.S., & Wong, W.K. (2010). A pseudo-Bayesian model in financial decision making with implications to market volatility, under- and overreaction. European Journal of Operational Research, 203(1), 166-175.
79. Lam, K., Liu, T.S., & Wong, W.K. (2012). A new pseudo bayesian model with implications to financial anomalies and investors' behaviors. Journal of Behavioral Finance, 13(2), 93-107.
80. Le, H.T.T., & Wong, W.K. (2019). A study on the factors affecting a firm's capital structure decision: A case study at Petro Vietnam. Journal of Advanced Research in Dynamical and Control Systems, 11(5), 834-845.
81. Leung, P.L., Ng, H.Y., & Wong, W.K. (2012). an improved estimation to make markowitz's portfolio optimization theory users friendly and estimation accurate with application on the us stock market investment. European Journal of Operational Research, 222(1), 85-95.
82. Lean, H.H., McAleer, M., & Wong, W.K. (2010). Market efficiency of oil spot and futures: A mean-variance and stochastic dominance approach. Energy Economics, 32, 979-986.
83. Lean, H.H., Phoon, K.F., & Wong, W.K. (2012). Stochastic dominance analysis of CTA funds. Review of Quantitative Finance and Accounting, 40(1), 155-170.
84. Lean, H.H., Smyth, R., & Wong, W.K. (2007). Revisiting calendar anomalies in Asian stock markets using a stochastic dominance approach. Journal of Multinational Financial Management, 17(2), 125–141.
85. Leung, P.L., & Wong, W.K. (2008). On testing the equality of the multiple Sharpe ratios, with application on the evaluation of Ishares. Journal of Risk, 10(3), 1-16.
86. Leung, P.L., & Wong, W.K. (2008a), Three-factor profile analysis with GARCH innovations. Mathematics and Computers in Simulation, 77(1), 1-8.
87. Li, C.K., & Wong, W.K. (1999). Extension of stochastic dominance theory to random variables. RAIRO-Operations Research, 33(4), 509-524.
88. Li, G., Mahmoudi, M.R., Qasem, S.N., Tuan, B.A., & Pho, K.H. (2020). Cluster ensemble of valid small clusters. Journal of Intelligent & Fuzzy Systems, 39(1), 525-542.
89. Lieberman, O., & Phillips, P.C. (2017). A multivariate stochastic unit root model with an application to derivative pricing. Journal of Econometrics, 196(1), 99-110.
90. Liu, J., Blocher, J.M., Armfield, S., & Moore, E. (2017). Modified flipped classroom: A project-based spiraling curriculum model to support learning efficiency and engagement. In Society for Information Technology & Teacher Education International Conference, 2391-2396.
91. Lo, F.Y., Wong, W.K., & Geovani, J. (2021). Optimal combinations of factors influencing the sustainability of taiwanese firms. International Journal of Emerging Markets, forthcoming.
92. Lozza, S.O., Wong, W.K., Fabozzi, F.J., & Egozcue, M. (2018). Diversification versus optimal: Is there really a diversification puzzle? Applied Economics, 50(43), 4671-4693.
93. Lu, R., Hoang, V.T., Wong, W.K. (2020) Lump-Sum Investing Strategy Outperform Dollar-Cost Averaging Strategy in Uptrend Markets?, Studies in Economics and Finance, forthcoming.
94. Lu, R., Yang, C.C., Wong, W.K. (2018). Time Diversification: Perspectives from the Economic Index of Riskiness. Annals of Financial Economics, 13(3), 1850011.
95. Lv, Z.H., Chu, A.M.Y., McAleer, M., Wong, W.K. 2019, Modelling Economic Growth, Carbon Emissions, and Fossil Fuel Consumption in China: Cointegration and Multivariate Causality. International Journal of Environmental Research and Public Health, 6(21). E4176.
96. Ly, S., Pho, K.H., Ly, S., & Wong, W.K. (2019a). Determining distribution for the product of random variables by using copulas. Risks, 7(1), 23.
97. Ly, S., Pho, K.H., Ly, S., & Wong, W.K. (2019b). Determining distribution for the quotients of dependent and independent random variables by using copulas. Journal of Risk and Financial Management, 12(1), 42.
98. Ma, C., & Wong, W.K., (2010). Stochastic dominance and risk measure: A decision-theoretic foundation for VaR and C-VaR. European Journal of Operational Research, 207(2), 927-935.
99. Ma, C., & Wong, W.K. (2021). A theoretical foundation for games of complete/incomplete contracts. International Journal of Financial Engineering, forthcoming.
100. Manzur, M., Wong, W.K., & Chau, I.C. (1999). Measuring international competitiveness: Experience from East Asia. Applied Economics, 31(11), 1383-1391.
101. Mahmoudi, M.R., Heydari, M.H., Avazzadeh, Z., & Pho, K.H. (2020). Goodness of fit test for almost cyclostationary processes. Digital Signal Processing, 96, 102597.
102. Maleki, M., Mahmoudi, M.R., Heydari, M.H., & Pho, K.H. (2020a). Modeling and forecasting the spread and death rate of coronavirus (COVID-19) in the world using time series models. Chaos, Solitons & Fractals, 110151.
103. Maleki, M., Mahmoudi, M.R., Wraith, D., & Pho, K.H. (2020b). Time series modelling to forecast the confirmed and recovered cases of COVID-19. Travel Medicine and Infectious Disease, 101742.
104. McAleer, M., Suen, J., & Wong, W.K. (2016). Profiteering from the Dot-com Bubble, Subprime Crisis and Asian Financial Crisis. Japanese Economic Review, 67(3), 257-279.
105. Moslehpour, M., Bilgicli, I., Wong, W.K., & Hua-Le, Q.-X. (2018). Meeting the agricultural logistics requirements of accommodation enterprises in Sakarya, Turkey. Journal of Management Information and Decision Sciences, 21(1).
106. Murthy, A., & Manthiram, A. (2012). Application of derivative voltammetry in the analysis of methanol oxidation reaction. The Journal of Physical Chemistry C, 116(5), 3827-3832.
107. Ng, P., Wong, W.K., & Xiao, Z.J. (2017). Stochastic dominance via quantile regression with applications to investigate arbitrage opportunity and market efficiency. European Journal of Operational Research, 261(2), 666-678.
108. Nguyen, H.H., Tuan, B.A., Thao, T.T.T., & Wong, W.K. (2019a). Teaching mathematics by practical decision modeling in Vietnam high schools to serve the fourth industrial revolution. Journal of Management Information and Decision Sciences, 22(4), 444-461.
109. Nguyen, T.H., Lin, K.H., Rahman, F.F., Ou, J.P., & Wong, W.K. (2020a). Study of depression, anxiety, and social media addiction among undergraduate students. Journal of Management Information and Decision Sciences, 23(4), 284-303.
110. Nguyen, T.T., Huynh, T.L.D., & Wong, W.K. (2019b). Factors driving openness in China trade: Corruption, exchange rate volatility, and macro determinants. Review of Pacific Basin Financial Markets and Policies, forthcoming.
111. Nguyen, T.T.H., Moslepour, M., Vo, T.T.V., & Wong, W.K. (2020b). State ownership, profitability, risk-taking behavior, and investment: An empirical approach to get better trading strategy for listed corporates in Vietnam. Economies, 8(2), 46
112. Ninomiya, S., & Victoir, N. (2008). Weak approximation of stochastic differential equations and application to derivative pricing. Applied Mathematical Finance, 15(2), 107-121.
113. Niu, C.Z., Guo, X., McAleer, M., & Wong, W.K. (2018). Theory and application of an economic performance measure of risk. International Review of Economics & Finance, 56, 383-396.
114. Niu, C.Z., Wong, W.K., & Xu, Q.F. (2017). Kappa ratios and (higher-order) stochastic dominance. Risk Management, 19(3), 245–253.
115. Owyong, D., Wong, W.K., & Horowitz, I. (2015). Cointegration and causality among the onshore and offshore markets for china's currency. Journal of Asian Economics, 41, 20-38.
116. Osler, T.J. (1970). The fractional derivative of a composite function. SIAM Journal on Mathematical Analysis, 1(2), 288-293.
117. Penm, J.H.W., Terrell, R.D., & Wong, W.K. (2003). Causality and cointegration, tests in the framework of a single zero-non-zero vector time series modelling. Journal of Applied Sciences, 3(4), 247-255.
118. Pho, K.H., Fu, Z., Mahmoudi, M.R., & Tuan, B.A. (2020). Prediction for the processes with almost cyclostationary structure. Journal of Statistical Computation and Simulation, 1-9.
119. Pho, K.H., Heydari, M.H., Tuan, B.A., & Mahmoudi, M.R. (2020). Numerical study of nonlinear 2D optimal control problems with multi-term variable-order fractional derivatives in the Atangana-Baleanu-Caputo sense. Chaos, Solitons & Fractals, 134, 109695.
120. Pho, K.H., Ly, L.Y., Hoang, T.H.V., Wong, W.K. (2021). Is Bitcoin a better portfolio diversifier than gold? A copula and risk analysis for China. International Review of Financial Analysis, 74, 101674.
121. Pho, K.H., Ly, S., Ly, S., & Lukusa, T.M. (2019). Comparison among Akaike information criterion, Bayesian information criterion and Vuong's test in model selection: A case study of violated speed regulation in Taiwan. Journal of Advanced Engineering and Computation, 3(1), 293-303.
122. Pho, K.H., Sarshad, M., Alizadeh, P., & Mahmoudi, M.R. (2020). Soil carbon pool changes following semi-arid lands planting programs. CATENA, 191, 104563.
123. Plakandaras, V., Gupta, R., & Wong, W.K. (2019). Point and density forecasts of oil returns: The role of geopolitical risks. Resources Policy, 62, 580-587.
124. Qiao, Z., Clark, E., & Wong, W.K. (2012). Investors’ preference towards risk: Evidence from the Taiwan stock and stock index futures markets. Accounting Finance, 54(1), 251-274.
125. Qiao, Z., Li, Y.M., & Wong, W.K. (2008). Policy change and lead-lag relations among china's segmented stock markets. Journal of Multinational Financial Management, 18, 276-289.
126. Qiao, Z., McAleer, M., & Wong, W.K. (2009). Linear and nonlinear causality between changes in consumption and consumer attitudes. Economics Letters, 102(3), 161-164.
127. Qiao, Z., & Wong, W.K. (2015). Which is a better investment choice in the Hong Kong residential property market: A big or small property? Applied Economics, 47(16), 1670-1685.
128. Qiao, Z., Wong, W.K., & Fung, J.K.W. (2013). Stochastic dominance relationships between stock and stock index futures markets: International evidence. Economic Modelling, 33, 552-559.
129. Salamzadeh, A. (2020). What constitutes a theoretical contribution? Journal of Organizational Culture, Communications and Conflict, 24(1), 1-2.
130. Salamzadeh, A., Farsi, J.Y., & Salamzadeh, Y. (2013). Entrepreneurial universities in Iran: A system dynamics model. International Journal of Entrepreneurship and Small Business, 20(4), 420-445.
131. Scalas, E. (2006). The application of continuous-time random walks in finance and economics. Physica A: Statistical Mechanics and its Applications, 362(2), 225-239.
132. Sergis, S., Sampson, D.G., & Pelliccione, L. (2018). Investigating the impact of flipped classroom on students' learning experiences: A self-determination theory approach. Computers in Human Behavior, 78, 368-378.
133. Suu, N.D., Luu, T.Q., Pho, K.H., & McAleer, M. (2020). Net interest margin of commercial banks in Vietnam. Advances in Decision Sciences, 24(1), 1-27.
134. Tajpour, M., & Salamzadeh, A. (2019). The effect of spiritual intelligence on organisational entrepreneurship: Case study of educational departments in University of Tehran. International Journal of Management and Enterprise Development, 18(3), 205-218.
135. Thanh, D.T. (2018). Teaching high-class homework solving oriented education comprehensive views for students. Journal of Science of HNUE, 63(5), 39-49.
136. Thanh, N.T., & Dung, N.T. (2015). Project based learning with flipped classroom model in B-learning. Journal of Science of HNUE, 60(8A), 222-230.
137. Thipwong, P., Wong, W.K., & Huang, W.T. (2020a). Kano model analysis for five-star hotels in Chiang Mai, Thailand. Journal of Management Information and Decision Sciences, 23(1), 1-6.
138. Thipwong, P., Wong, WK., & Huang, WT. (2020b). The impact comparison of supply chain relationship on public transportation quality in Taichung city, Taiwan and Chiang Mai city, Thailand. Journal of Management Information and Decision Sciences, 23(1), 16-34.
139. Tiku, M.L., & Wong, W.K. (1998). Testing for unit root in AR(1) model using three and four moment approximations. Communications in Statistics: Simulation and Computation, 27(1), 185-198.
140. Tiku, M.L., Wong W.K., & Bian, G. (1999). Time series models with asymmetric innovations. Communications in Statistics: Theory and Methods, 28(6), 1331-1360.
141. Tiku, M.L., Wong, W.K., Vaughan, D.C., & Bian, G. (2000). Time series models in non-normal situations: Symmetric innovations. Journal of Time Series Analysis, 21, 571-96.
142. Tran, D.T., Wong, W.K., Moslehpour, M., & Xuan, Q.L.H. (2019). Speculating environmental sustainability strategy for logistics service providers based on DHL experiences. Journal of Management Information and Decision Sciences, 22(4), 415-443.
143. Tsang, C.K., Wong, W.K., & Horowitz, I. (2016). Arbitrage opportunities, efficiency, and the role of risk preferences in the Hong Kong property market. Studies in Economics and Finance, 33(4), 735-754.
144. Tuan, B.A., Pho, K.H., Huy, L.M., & Wong, W.K. (2019). Stemtech model in Asean Universities: An empirical research at can Tho University. Journal of Management Information and Decision Sciences, 22(2), 107-127.
145. Tung, N.T. (2015). Teaching integrated with the subjects of medicine statistics, informatics and scientific research in the Universities of Medicine and Pharmacy. Journal of Science of HNUE, 60(8A), 187-192.
146. Valenzuela, M.R., Wong, W.K., & Zhu, Z.Z. (2020). Sources of inequality in the Philippines: Insights from stochastic dominance tests for richness and poorness, World Economy, 43(10), 2650-2673.
147. Vieito, J.P., Batmunkh, M.U., Choijil, E., Espinosa, C., & Wong, W.K. (2020). Does herding behavior exist in the mongolian stock market. Pacific-Basin Finance Journal, 62, 101-352.
148. Vieito, J.P., Wong, W.K., & Zhu, Z.Z. (2015). Could the global financial crisis improve the performance of the G7 stocks markets? Applied Economics, 48(12), 1066-1080.
149. Yadav, S., Pandey, R.K., & Shukla, A.K. (2019). Numerical approximations of Atangana–Baleanu Caputo derivative and its application. Chaos, Solitons & Fractals, 118, 58-64.
150. Wengert, R.E. (1964). A simple automatic derivative evaluation program. Communications of the ACM, 7(8), 463-464.
151. Wong, W.K. (2007). Stochastic dominance and mean-variance measures of profit and loss for business planning and investment. European Journal of Operational Research, 182(2), 829-843.
152. Wong, W.K., & Bian G. (2005). Estimating parameters in autoregressive models with asymmetric innovations. Statistics and Probability Letters, 71(1), 61-70.
153. Wong, W.K., & Chan, R. (2004). On the estimation of cost of capital and its reliability. Quantitative Finance, 4(3), 365-372.
154. Wong, W.K., & Chan, R. (2008). Prospect and markowitz stochastic dominance. Annals of Finance, 4(1), 105-129.
155. Wong, W.K., Lean, H.H., McAleer, M., & Tsai, F.T. (2018). Why are warrant markets sustained in taiwan but not in china? Sustainability, 10(10), 3748.
156. Wong, W.K., & Li, C.K. (1999). A note on convex stochastic dominance. Economics Letters, 62, 293-300.
157. Wong, W.K., & Ma, C. (2008). Preferences over location-scale family. Economic Theory, 37(1), 119-146.
158. Wong, W.K., & Miller R.B. (1990). Analysis of ARIMA-noise models with repeated time series. Journal of Business and Economic Statistics, 8(2), 243-250.
159. Wong, W.K., Phoon, K.F., & Lean, H.H. (2008). Stochastic dominance analysis of Asian hedge funds. Pacific-Basin Finance Journal, 16(3), 204-223.
160. Woo, C.K., Wong, W.K., Horowitz, I., & Chan, H.L. (2012). Managing a scarce resource in a growing Asian economy: Water usage in Hong Kong. Journal of Asian Economics, 23(4), 374–382.
161. Yousaf, I., Ali, S., & Wong, W.K. (2020). Return and Volatility transmission between world-leading and Latin American stock markets: portfolio implications. Journal of Risk and Financial Management, 13(7), 148.
162. Yuan, X., Tang, J., Wong, W.K., & Sriboonchitta, S. (2020). Modeling co-movement among different agricultural commodity markets: A copula-GARCH approach. Sustainability, 12, 393.
163. Zhu, Z.Z., Bai, Z.D., Vieito, J.P., & Wong, W.K. (2019). The impact of the global financial crisis on the efficiency of latin American stock markets. Estudios de Economía, 46(1), 5-30.