Keywords

Transshipment Policies, Complete Pooling, Partial Pooling, Simulation, Vendor-Managed Inventory, Supply Chain Management, Partial-Pooling Threshold.

Introduction

Logistics is now widely recognized as a value-added center in organizations thanks to product availability, consistency of deliveries, accuracy of inventory, demand modeling and ease of order schedules. Vendor-Managed Inventory (VMI) is one of the most recent examples of adding value through logistics. This practice provides a streamlined approach to inventory management in which the supplier makes replenishment decisions based on specific inventory and supply chain policies. VMI is often described as a winning situation: Suppliers manage distribution and production costs as they can combine and coordinate requests and shipments for different customers and also help manage inventory control by targeting to ameliorate the global profit of the business and society.

In this paper, we consider a centralized one-echelon supply chain with two-retailers selling products and facing stochastic demand. Given the large distance between the supplier and retailers, and the corresponding large fixed transportation cost (by order) long replenishment cycles are typically used. In such situations, transporting stocks between retailers is much easier and less costly, and may be done on a more frequent basis. In this work, we therefore explore what the cost benefits are of allowing multiple shipments between retailers during a supplier replenishment cycle. Items’ trans-shipment between retailers still involves of course certain costs, in particular for handling and moving the items. Since multiple items can often be shipped on a single pallet, part of those costs will be independent of the number of items shipped. Instead of only including a variable transport cost per item, as is done by (Bouma et al., 2014) we will therefore also include a fixed transport cost per shipment.

Literature Review

Effective supply chain management is now recognized as a key element of competitiveness and success in most industrial enterprises. However, since the network that makes up the supply chain is usually too complex to analyze and optimize on a large scale, it is often preferable to focus on smaller parts of the system so as to gain a full understanding of its characteristics and performance. Each component of the same level manages its stock in a independent to each other. Such attention is paid to this network because of its complexity (uncertainty of demand, lead time, etc.) which increases significantly. The overall performance of the storage network, whether evaluated in economic terms or in terms of customer service, can be significantly improved if sites (retailers, outlets, stores) work together in this random environment. Collaboration between sites is defined as cooperation where collaborating sites share their stocks when needed. Generally, the collaboration is made laterally (in the same echelon) from a site which has a surplus of stock to another which faces a shortage of stock: what is called lateral transshipment. Collaboration could be an effective way to improve the logistics performance of the company without any need for additional cost. As the cost of lateral transfer of items between sites is generally much lower than the cost of shortage and the cost of emergency delivery from central warehouse, and the lateral transfer time is shorter than the regular replenishment lead time, so the collaboration could reduce the total system cost and improve the level of service for customers. There are two types of collaboration: emergency collaboration and preventive collaboration. The goal of the emergency collaboration, which takes place after receipt of the demand, is to address current disruptions in inventory. While, preventive collaboration which is done before receiving customer demand, aims to reduce the risk of having stock-out in the future. Collaboration can also be classified according to the quantity to be transferred: there is full collaboration where the site offers all its available stock when another site faces a stock-out and partial collaboration where the site keeps part of the stock to cover future demand.

Several quantitative decision support models are proposed in the literature to study the impact of lateral transfer between sites. These models can be classified according to several characteristics: (1) the structure of the network (2) the type of optimization model.

In the articles reviewed Derhami et al. (2020), Wong et al. (2005), Yong (2009), there are at least six important criteria which are taken into consideration in a comprehensive study of the subject:

1. The number of collaborators in the group,

2. The time of replenishment from the central warehouse,

3. The profile of the request,

4. The time (before or after receipt of the request) and the purpose of the collaboration (emergency or preventive),

5. Reparability of stored items and

6. Performance measures (cost or level of service).

A large number of works focus in their research on the type of lateral transshipment, i.e. Emergency transhipment or preventive transhipment.

Herer et al. (2002) analyzed the emergency lateral transshipment strategy between two-retailers and found this last can simultaneously improve lightness and agility. Paterson et al. (2012) and Noham & Tzur (2014) respectively developed a quasi-myopic approach and a simple heuristic algorithm. Van et al. (2009) have presented models where preventive collaboration takes place before receipt of the request in order to have a better distribution of stock available between the different collaborators.

Archibald et al. (2009) studied an inventory system considering that basic stock is ordered, while the decision to place an emergency order from the warehouse or to use lateral transfer depends on the costs, the time remaining in the warehouse. The period and inventory available in the alternative site. Relaxing the hypothesis of the instant central warehouse replenishment time considerably complicates the mathematical analysis of the network because of the interrelationships between demand, quantities to be transferred and stock in transit. In particular, if the optimal transfer strategy should take into account both on-hand and on-order inventory, implying that state space should be increased. In addition, full collaboration assuming that the lead time is negligible and where the costs across the sites are the same is not necessarily optimal when the lead time is positive. Therefore, the decision space is more complex and the exact model becomes intractable even in the simple case (two-retailers). Li et al. (2013) aim to study the effect of preventive lateral transhipment on the quantities ordered in a two-echelon inventory system. Liao et al. (2014) studied a comparison between side transfer and emergency order options. The sharing is done in a bidirectional way to coordinate the transhipment quantities. Olsson (2015) studied a lateral transshipment policy for a two-retailer inventory system with a positive transshipment delay. A more sophisticated transhipment policy has been developed, the results of which show that it is worthwhile to reduce transhipment times. Torabi et al. (2015) analyzed a problem of an inventory system in an e-commerce environment with complete-pooling. A mixed integer programming model has been formulated and solved to minimize logistics costs. Lee & Park (2016) studied an inventory model with two retailers and a single supplier with uncertain capacity. By applying lateral transshipment, they found that a transshipment price may be able to coordinate the supply chain. Feng et al. (2017) discussed a dynamic problem of preventive lateral transshipment in a centralized inventory system based on Markov decision making. They used simulation to study the inventory system with significant reorder time and different costs. The authors conclude that full collaboration is less expensive than partial collaboration. They also provided approximations for on-hand inventory, shortage inventory, and transfer inventory as well as heuristics to determine a near-optimal reorder point solution under full collaboration. Silbermayr et al. (2017) investigated the problem of emergency lateral transshipment with environmental sustainability. The research of Nakandala et al. (2017) focuses on the study of an emergency lateral transshipment model for perishable products in a fresh produce supply chain. This research is concerned with applying a more comprehensive transshipment decision method to help the practitioner make profitable decisions. Timajchi et al. (2019) discussed an inventory flow problem with a transshipment of pharmaceutical items. Feng et al. (2018) analyzed such advanced research to study emergency lateral transshipment and preventive transshipment in a comparable partially delayed setting. Dehghani & Abbasi (2018) propose a policy of emergency transshipment of perishable foodstuffs in supply chains. They developed a heuristic solution to calculate performance metrics. Timajchi et al. (2019) analyzed deterioration in pharmaceuticals and proposed a side-shift option to meet demand while simultaneously minimizing costs and accidental losses. Yi et al. (2020) found the optimal emergency transshipment and replenishment decisions within a decentralized inventory system framework. They build a multistep stochastic model that captures the uncertainty of demand and changing customer behaviour.

Problem Description

We are targeting to improve the global profitability of stock system composed of two retailers by minimizing the Des-service rate of each site by decreasing the quantity out of stock. This result in the improvement of the Average Global Profit in the whole inventory system this can be done by applying the cooperation between these retailers which is called by the transshipment, either by the application of the policy of transhipment: “Complete-Pooling” or “Partial-Pooling”. Each time we modified the threshold of the "Partial-Pooling" transshipment policy, the periodicity T and the unit cost of transshipment. We consider a distribution system consisting of two retailers no-identical (i=1, 2) owned or operated by the same entity and one manufacturer that sells to these retailers in a single period. Following the newsvendor scenario, the central depot owner needs to decide, for retailer n, a no negative order quantity Q_i, before observing demand Di, with i=1,2. Let 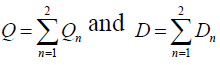we assume that the distribution center shares orders for a single product within a fixed period (control period), and this regardless of the quantities of supply.

To solve this type of problem, we can apply the "Without-Transshipment" policy, that is to say, when the retailer falls into an out-of-stock position, he demands the quantity of central deposit missing to satisfy customer demand, or, by applying the "With-Transshipment" policy, by adopting a relationship between the retailers who are in the same line to minimize the stock shortage and meet a random demand. In this paper we will try to find the most appealing controversy that aims to maximize the expected Average Global Profit and minimize as much as possible the Average Global Disservice Rate.

Modeling Mathematical

We use the periodic storage policy (R,Si) for each retailer i=1,2.

The inventory control period, R, is composed by T time intervals separated by two successive client demand for each retailer 1≠2.

According to this policy, at the end of each revision period R (assumed to be 28 days, according to Meissner & Rusyaeva (2016), if the retailer's stock position (noted PSi=available stock-demand) falls below a given value, called replenishment level, then a replenishment order is initiated from the central repository so as to bring that stock position back to initial position. The order is received at the end of the supply period.

The quantity of supply within time intervals T is then expressed by the equation 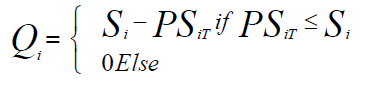1.

(1)

The demand Di at the retailer i during a period R is a random variable that follows the normal distribution with mean μn and standard deviation σn. We make the assumption that the demands at the retailers are independent and identically distributed (i.i.d).

When this demand causes a stock out during the period of the check at the retailer 1, then transshipment will be made from the retailer 2 to 1, the amount of transshipment will be noted by X₂₁. We suppose, too, that the transshipment time is zero and that the unit cost of the transshipment noted C is a linear cost according to the amount transferred between the retailers. Finally, we assume that partial satisfaction of customer demand by the retailer is not allowed and that claims that can’t be satisfied by the available stock and the transshipment are lost and are subject to a cost of break noted C_p per unit lost. In all cases, the available stock becomes zero and will remain zero until the next supply. The mathematical modeling that we study in the following paragraph, concerns a transshipment system composed of two non-identical retailers. The approach we have adopted is inspired from the work of (Emel & Lena, 2017). Recall that these researchers solved a problem of a stock system (R, S_i) by considering a single central repository and two retailers. Our goal is to begin by identifying the difficulties to be met by the resolution of an inventory system by introducing transshipment in order to identify procedures of resolution for a large number of retailers.

Parameters

The notations used in this paper are as follows:

n: Number of retailers; i: Retailer index (counter) with i=1, 2 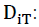Demand during the periodicity T at the retailer i (random variable) follows the normal law ( , ).These demands are independent and identically distributed (i.i.d) 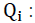The quantity of supply for the retailer i R: Inventory position revision period, which is divided into k intervals of time of periodicity T; 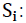Maximum level of stock at retailer i at the start of the supply cycle;

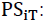Stock position at retailer i at each time period T

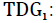Average Global Desservice Rate for i retailers

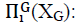Average Global Profit for the two retailers i, with i=1,2

Vi : Unit selling price for each site i, with i=1,2

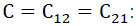Unit cost of transshipment whatever the direction of lateral transfer,

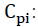Unit cost of shortage for such a site i.

Modeling and Experimentation

The resolution of our problem is fundamentally based on the probabilistic behaviour of customer demands. It is a continuous distribution which follows the normal law.

For this, among the sampling techniques that allow an exploration of customer demand, we selected the simulation. Its principle is then to select, for each demand, random values determined according to an average and a standard deviation. In addition, the demand is generated independently time and between retailers.

We will then, model in this paper, Two-Retail Stock Distribution System, successively appointed “Without-Transshipment” and “With-Transshipment”. The latter, may be in the form of a transshipment policy called "Complete-Pooling ", if the retailer agrees to transfer all of its available stock if necessary, or by "Partial-Pooling", if the transshipment is carried out by preserving a targeted stock level, by modifying the threshold beyond which the retailer agrees to apply trans-shipment for each experience. First, the latter will be set at a value which is equal to two times the demand (this is that is to say, to protect the next two demand), then it will be equal, to the next demand and finally it is worth to a safety stock which equals 30% of stock position.

Case “Without-Transshipment”

Conceptual Model

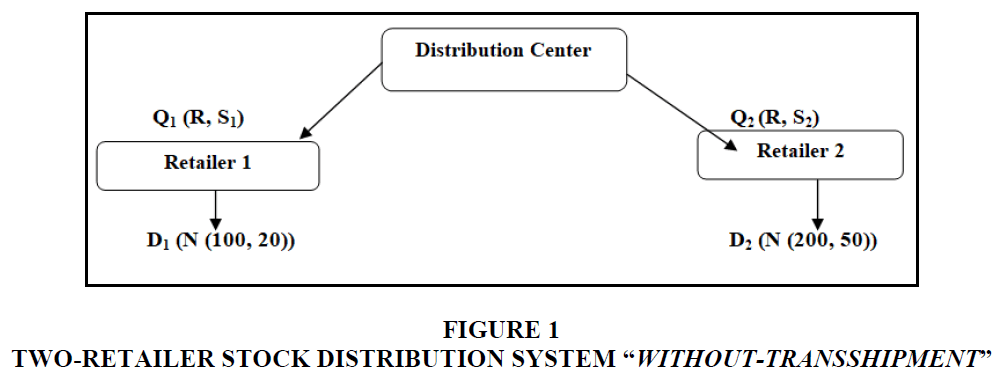
In this case, if the retailer is confronted with a random demand and to satisfy it and does not fall out of stock, he must demand the missing quantity from the central deposit.

This can be represented by Figure 1.

For the Without-Transshipment (No-Pooling) case, the modeling by the ARENA 16.0 software can be presented by the Figure 2.

Assumptions

To properly model this stock system using the Arena software, it is necessary to list the assumptions and the mode of operation retained in this work:

• The storage capacity of the central warehouse is infinite

• Retailer i applies the storage policy (R, S_i)

• Partial satisfaction of an order is not allowed

• Any unsatisfied order will be lost

• Only one order (emergency according to the central depot) is allowed per supply cycle (at the end of period R); with R=kT

• There is no definite order of priority. All customer orders are managed according to the same FCFS (First Coming First Served) priority rule

• The distribution center has sufficient storage capacity, so as not to introduce availability constraints (Unlimited storage policy)

• At the start of each supply cycle, a size order Qi, 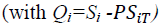is placed to reach the stock level noted S_i.

Mathematical Function of Average Global Profit

The Average Global Profit function of our centralized inventory system for two “Without- Transshipment” retailers contains the selling price of the customer product and the cost of the shortage. It takes the general form of the equation 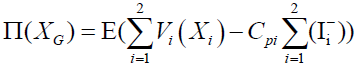2.

(2)

Case “With-Transshipment”

Conceptual Model

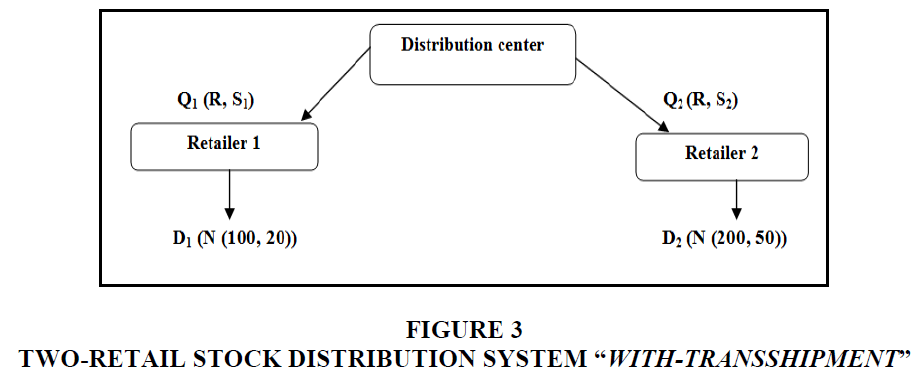
If one of the two retailers is in the out-of-stock position, then cooperation can be established between them to meet their random demand. This collaboration usually takes the form of "Transshipment-Lateral", also quite simply known as "Transshipment" (Figure 3), which allows stocks to be pooled to alleviate the uncertainties relating to demands arriving at sites of the same level.

In this section, we will study two transshipment policies successively named "Complete- Pooling" and "Partial-Pooling".

Transshipment Policies

Complete-Pooling

For the first trans-shipment policy called “Complete-Pooling” the modeling by the ARENA 16.0 software can be presented in Figure 4.

Assumptions

We consider the following assumptions:

• Retailer 1 confronts a random demand independent of demands from retailer 2;

• The transshipment time is zero;

• In the case where a retailer 1 faces a stock shortage, whereas, the retailer 2 has a surplus of inventory, a transshipment of the necessary quantity 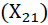will take place from 2 to 1 to avoid or minimize the shortage: this is the correct transshipment (also called reactive transshipment). Otherwise depot 1 may require an emergency order of size Q1 at the distribution center;

• In the event of "Complete-Pooling", the retailer who is in the overstock position agrees to transfer all of his available stock if necessary.

Mathematical Function of Average Global Profit

The function of Average Global Profit for our centralized system composed of two levels and two retailers, by integrating transshipment and applying the "Complete-Pooling" policy, can be formulated by the equation 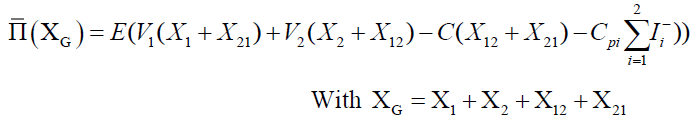3.

(3)

Quantity of Trans-shipment

We assume that retailer 1 is the one facing a stock shortage, so according to this transshipment policy, retailer 2 agrees to transfer all of its available stock if necessary, even if this stock is not enough to fill any the demand of the client who is at the origin of the demand for the transshipment. The quantity of the transshipment, according to this policy, will be formulated in the form of the equation 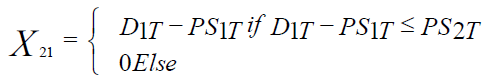4.

(4)

Objective Function

The objective is to identify the most economically profitable transshipment policy for a centralized system over a finite time horizon R, by seeking the lowest possible Average Global Des-service Rate.

For this, the objective function of the "Complete-Pooling" transshipment policy will be defined in the form of the equation 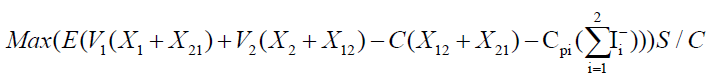(5).

(5)

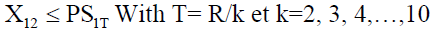
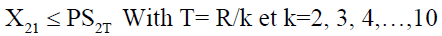
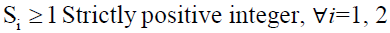
With,

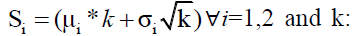being the number of periodicities, aveg k=2, 3, 4,…,10 and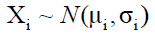

Partial-Pooling

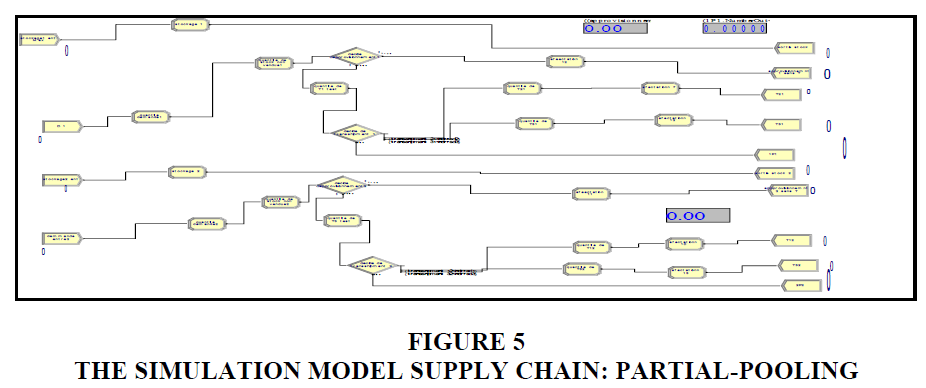
For the second transshipment policy called “Partial-Pooling” the modeling by the ARENA 16.0 software can be presented in Figure 5.

Assumptions

Furthermore, the hypotheses already indicated for the “Complete-Pooling” transshipment policy, we can add another specific assumption for the “Partial-Pooling” policy, that is, the lateral transfer is carried out while preserving a level of targeted stock. We find in research work the following variants:

1. The retailer accepts the transshipment up to the amount of surplus stock to its safety stock,

2. The retailer accepts the transshipment up to the amount of surplus stock at his order point,

3. The retailer accepts the transshipment up to the amount of surplus stock at the estimated demand for the following period (Archibald et al., 2009).

4. The decision to make transshipment at the level of a retailer depends on the current stock level and the time remaining before the next supply.

In our paper, we are interested in the third variant where the retailer accepts the transshipment up to the amount of surplus demand for a first proposal of the threshold value. Then we add two other personal contributions, first estimating that it will be equal to "Two multiply by demand". Secondly, it will be equal to “30% of stock position”, to improve the Average Global Profit of the entire system made up of two retailers while minimizing as far as possible the average stock-out (Average Global Des-service Rate).

In the following sections of this paper, we first describe the mathematical modeling of a "Sans-Transshipment" stock system for a warehouse number set to two. Then we modify it, by integrating, the two policies of transshipment, named, successively, "Complete-Pooling" and "Partial-Pooling".

Mathematical Function of Average Global Profit

The function of the average global profit apply the transshipment policy "Partial- Pooling", requires the integration of the quantity lost for each retailer after the accumulation of stock. The average global profit function will be formulated by the equation 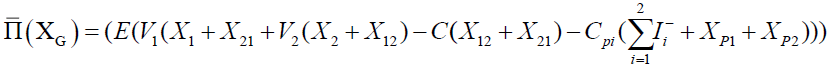6.

(6)

With,

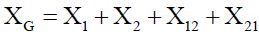
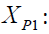The quantity lost for retailer 1 after the accumulation of stock with partial transshipment.

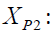The quantity lost for retailer 2 after the accumulation of stock with partial transshipment.

Quantity of Transhipment

To significantly improve a purely reactive transshipment policy, it would be possible to combine it with another proactive policy; this will be named by “Hybrid transshipment policy”. In this area of research, the policy of transshipment "Partial-Pooling", to put the action on the importance of the estimate of the future to minimize as soon as possible the quantity not satisfied which governs positively on the economic profitability.

We estimate that retailer 1 is facing an actual stock shortage, therefore, the amount of lateral transfer from retailer 2 to 1 to minimize or avoid this lost quantity, according to this transshipment policy will be carried out while preserving a targeted stock level. Named the transshipment threshold and it will be formulated by three equations according to the fixing of the latter.

First of all, we estimate that it will be worth to twice multiply by the Demand, for this, the quantity of transshipment from 2 to 1 will be formulated by the equation 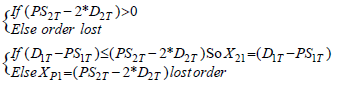7.

(7)

Then we assume that this threshold is equal to the Next Demand, and then the amount of lateral transfer from 2 to 1 will be formulated by the equation 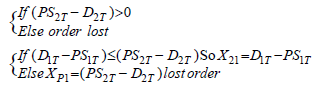8.

(8)

Finally, we propose that it be equal to a safety stock which is worth 30% of therefore, the amount of transshipment will be formulated by the equation 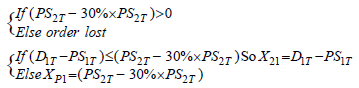9.

(9)

Objective Function

For the second transshipment policy (“Partial-Pooling”), the objective function will be defined in the form of the equation 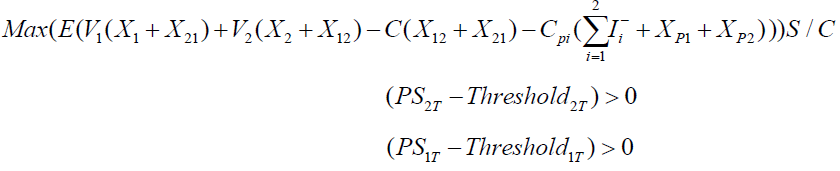(10).

(10)

With

Threshold_iT =Twice the Demand, Next Demand and 30% of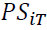

X_P1 : The quantity lost for retailer 1 after the accumulation of stock with partial transshipment.

X_P2 : The quantity lost for retailer 2 after the accumulation of stock with partial transshipment.

T= R/k et k=2, 3, 4,…,10.

S_i ≥ 1 Strictly positive integer, ∀i=1,2

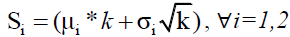and k: being the number of periodicities, With k=2, 3, 4,…,10.

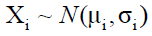
Characteristics of the Methodology Applied (Discrete Event Simulation)

Because of the limits of analytical resolution for certain aspects, remains complex and very difficult to solve. In particular, because the distribution of demand is random which makes the stock position for each retailer to be unknown and difficult to calculate, this leads us to resort to an approach by Discrete Event Simulation which we have given the possibility, at the same time, to relax the restrictive assumptions considered in the mathematical model and to analyze in a more detailed way the contributions of the transshipment and its sensitivity to different parameters (periodicity "T", threshold and unit cost of transshipment).

We describe, in the following section, the chosen resolution approach and the simulation model. Besides, in our research work we assume that customer demand is a random variable, which leads to the application of the discrete event simulation approach. It consists of computer modeling by applying ARENA software, where the change in the state of a stock system over time is a series of discrete events. Each event (random demand) occurs at a given time and changes the state of the system. Moreover, in this approach, we start by listing any events or state changes that may be encountered during the evolution of the inventory quantity. Then the logic of state changes is modeled in the form of algorithms by defining, for each type of event, the state conditions leading to the occurrence of the event as well as the corresponding state changes. The simulation of the stock system is obtained by executing the state change logics associated with each event on the date on which it occurs.

Simulation Results

We recall that, according to (Meissner & Rusyaeva, (2016)), the initial level of replenishment for a demand that follows the normal law of mean and standard deviation, will take the form of the equation and will be calculated by applying the Equation 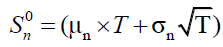11.

(11)

With

T: number of periods

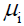: Average demand during the period T of retailer i, with i=1,2.

σi : Standard deviation of demand of retailer i, with i=1,2.

Table 1 shows the different measures of initial stock level of replication and for n=2, with N: number of retailers. Recall that the network structure considered in this paper is made up of a distribution center and two retailers, who face random and non-identical demands on average and standard deviation. We assume that the simulation length is 10 years.

Table 1 Determination of Different Measures of the Initial Level of Replenishment
k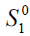
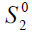2	229	470
3	335	687
4	440	900
5	545	1112
6	648	1322
7	753	1532
8	857	1741
9	960	1950
10	1063	2158

We have assumed that the demand D1 of the first retailer follows the law N(100, 20) and that of second retailer, D2 follows the law N(200, 50). These demands are Independent and identically distributed (i.i.d).

Also, we have considered in all the examples of our research that:

1. The revision period R = 28 days, (Based on (Emel & Lena, 2017));

2. The unit sale price for retailer 1 equal to 95 $ and that of retailer 2 is worth 125 $,

3. The unit cost of rupture whatever the site is equal to 30 $,

4. The unit cost of transshipment=3 $, 0.5 $, k = 2, 3, 4,…, 10.

We led to the resolution of our problem via simulation by successively testing the “Without trans-shipment” and “With-transshipment” policies. We then give the following performance measures, for the evaluation of the contribution to perform the Pooling between the retailers:

• The number of supply orders (without transshipment),

• The number of orders received with the transshipment application,

• The amount of lateral transfer from a warehouse which is in overstock position to that of the same level which is in rupture position,

• The quantity of order not fulfilled at a retailer (quantity lost),

• Average Global Profit at a retailer,

• The Average Des-service Rate (the rate of customer dissatisfaction after the transshipment).

In Table 1 we present the different measures of the initial stock level of the replenishment.

Impact of Input Parameters on Average Global Profit

We examine the effect of three input parameters on the benefits of transshipment, namely:

• The periodicity "T",

• The unit cost of trans-shipment,

• And, the threshold of the “Partial-Pooling” trans-shipment policy.

Impact of the Periodicity "T"

“Without-Transshipment” system vs. "With-Transshipment" system

The numbers calculated in Table 1 reveal the considerable effect of collaboration between the sites in terms of Average Global Profit.

Likewise, they present the results of the performance evaluation of the "Complete- Pooling" and "Partial-Pooling" transshipment policies compared to the "Sans-Transshipment" policy. We note, first, that these results verify those already obtained by the mathematical model for a stock system with two non-identical retailers, namely that:

• The comparative values obtained by simulation in Table 1, using the "ARENA" software, confirm the evidence of the advantage of the application of "transshipment" between the sites in terms of improving the Average Global Profit. For example, for k=2, "Complete-Pooling" improved the performance of the centralized inventory system by increasing the average value of Average Profit Global of the two retailers, from 39125 to 44087, that is to say, a relative change worth 13%,

• These values show the effect of the change in periodicity on economic profitability, by improving the Average Global Profit from k=2 to k=4. Whereas, the evolution of the value of the latter undergoes an imperfection beyond k=4, and this will be explicit for k=5 up to k=10, because, in these periodicities, this profit becomes under the shape of a decreasing curve because of the increase in the number of customer orders by the period R=28 days.

Complete-Pooling vs. Partial-Pooling

Comparative Average Global Profit Improvement Percentage Values Obtained by Simulation Using ARENA Software for the Two Transshipment Policies "Complete-Pooling" and "Partial-Pooling" are reported in Table 2.

Table 2 Determination of the Values of the Relative Improvement Percentage of the Average Global Profit for a Unit Cost of Transshipment=3$
k	Without trans-shipment / Complete-Pooling	Complete-Pooling/Partial-Pooling: Twice the Demand	Complete-Pooling/ Partial-Pooling: Next Demand	Complete-Pooling / Partial-Pooling: Security Stock=30% of PSiT
2	13%	3%	17%	26%
3	15%	2%	14%	18%
4	16%	1%	8%	11%

To calculate the different percentages of relative improvement in Average Global Profit indicated in Table 2, we apply the mathematical Equation 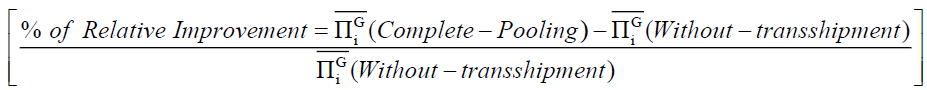12.

(12)

This for the first column of the table while for the two transshipment policies ("Complete- Pooling" and "Partial-Pooling") we apply this formula while looking for the percentage improvement value between them.

From Table 2, we see that, the percentage improvement in Average Global Profit depends on the periodicity T, as well as, on the transshipment policy applied, ("Complete-Pooling" or "Partial-Pooling").

We note that the first lateral transfer policy (“Complete-Pooling”) improves the economic profitability of the “No-transshipment” policy but with a percentage of improvement less than that of the transshipment policy (“Partial-Pooling”). Because of this, the latter is more advantageous, because the Average Global Profit of the former will be improved regardless of the threshold applied. We will conclude, too, that the modification of the latter acts on this improvement, take as an example, for k=2, the "Partial-Pooling" with a threshold of the "Twice the Demand" target to reach a percentage of improvement Relative Average Global Profit of "Complete-Pooling" equal to 3% but with the change of the threshold to "Next Demand" this value is worth 17% and finally for a threshold equal to "SS=30% of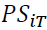 " and becomes equal to 26%. By analyzing the variation of the threshold of the “Partial-Pooling” transshipment policy, we note that if the latter is higher than this leads to reducing the chances of supply which results in an increase in the demand no satisfaction rate.

This allows us to conclude that the most economically profitable transshipment policy is that of "Partial-Pooling" and especially with a lateral transfer threshold equal to "SS = 30% of 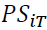". This observation leads to a first conclusion in our research, namely that the change of the threshold influences the percentage improvement relative to the Average Global Profit.

Impact of the Unit Cost of Trans-shipment and the Threshold for Trans-shipment

The study of the impact of the variation in the unit cost of transshipment on the Average Global Profit is carried out in cases where C=0.5$. The simulation results are presented in Table 3.

“Without-Transshipment” System vs. "With-Transshipment" System

We examine, for a stock system composed of two levels and two non-identical retailers, the impact of the variation in the unit cost of transshipment and the threshold of the "Partial-Pooling" policy.

The results of the simulation presented in Table 3 show that a variation in this unit cost of transshipment, by reducing it from 3$ to 0.5$, acts mainly on improving the profitability of the entire centralized system between the "Without-Transshipment" and that of "With-Transshipment", for that, we will conclude that, the coordination between the sites of the same level allows to improve the profitability of the whole system, but it reaches the most effective values by the application of the “Partial-Pooling” transshipment policy and above all with the fixing of the threshold at “security stock=30% of PS_iT”.

Table 3 Determination of the Average Global Profit for a Unit Cost of Transshipment=0.5$
k	Without-Transshipment	Complete-Pooling	Partial-Pooling
			Twice the Demand	Next Demand	Security Stock=30% of PSiT
2	39125	45054	46938	52502	56400
3	65044	75754	77740	85952	88976
4	88000	102306	103510	110200	113800
5	86240	101200	102520	105035	107097
6	83600	97657	99125	101257	103356
7	80960	94230	95127	96102	98235
8	78320	91560	93276	94605	97203
9	70400	82359	83900	88007	90102
10	66000	77135	79230	84009	87990

For this, we will first of all look for the relative improvement percentage of the Average Global Profit of the centralized system for the first “Complete-Pooling” transshipment policy by reducing this cost (Table 4), then by calculating it with the integration of the second “Partial- Pooling” policy (Table 5).

Table 4 Determination of the Percentage Improvement in Average Global Profit for "Complete Pooling" between C = 3 $ AND C = 0.5$
K	Percentage improvement in Average Global Profit (%)
2	2
3	2
4	1

Table 5 Determination of the Percentage Improvement in Average Global Profit for Partial Pooling Between C=3$ AND C=0.5$
k	Pourcentage du Profit Global Moyen
	Twice the Demand	Next Demand	Security Stock=30% of PSiT
2	3%	2%	2%
3	1%	1%	1%
4	1%	3%	2%

"Complete-Pooling" vs. "Partial-Pooling"

The determination of the various relative improvement percentage values of the Average Global Profit for the “Complete-Pooling” transshipment policy or (simply noted CP) between C=3$ and C=0.5$, is done by applying the Equation 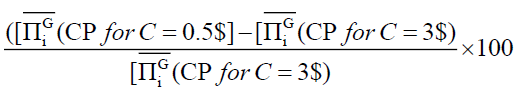13.

(13)

According to the Table 4, we quote for example that, for k=3 and with a unit cost of transshipment equal to 3$, the “Complete-Pooling” transshipment policy improved the value of average overall profit “Without-Transshipment” from 65044 to 74538, therefore with an improvement value equal to 15%.

But, with a slight reduction in the unit cost of transshipment, this percentage becomes equal to 17%. For this, we will conclude that the unit cost of transshipment has an influence on the improvement of the Average Global Profit of the whole centralized stock system.

From Table 5, we will conclude that the application of the unit cost of transshipment equal to 1 $ is more profitable in terms of gain compared to that which is worth 2 $, and this is remarkable from the results presented in this table, but with a small percentage of improvement.

For example,

• For a threshold=twice the Demand: the “Partial-Pooling” transshipment policy with a unit cost equal to 0.5$ makes it possible to improve the Average Global Profit of the one that equals 3$ with a minimum value equal to 1% up to a maximum value equal to 3%.

• For a threshold=Next Demand: With a unit cost of transshipment worth $0.5, the “Partial-Pooling” transshipment policy has improved the Average Global Profit by that which equals 3$ with a minimum value equal to 1% up to a maximum value equal to 3%.

• For a threshold=30% of PS_iT: With a unit cost of transshipment equal to 0.5$, the economic profitability of the centralized system for the policy of transshipment "Partial-Pooling" undergoes an evolution compared to that which equals 3$ of a minimum value equal to 1% up to a maximum value equal to 2%.

In fact, according to the study of the impact of the change in the unit cost of transshipment and the threshold of the “Partial-Pooling” policy on the improvement of Average Global Profit, the analysis of the sensitivity of performance to this variation can be summarized as follows:

• The decrease in the unit cost of transshipment influences the increase in the percentage of relative improvement in economic profitability.

• The evolution of Average Global Profit has a strong relationship with the modification of the threshold beyond which the retailer accepts the transshipment to design of available stock.

Impact of the input parameters on the Average Global Des-service Rate (The "T" periodicity and the transshipment threshold). We focus here on determining, the policy of transshipment in a centralized stock system which seeks to improve the Average Global Profit at the two retailers by minimizing the Average Global Des-service Rate as much as possible.

In this section of paper, we formulate the Average Global Desservice Rate for the two retailers by Equation 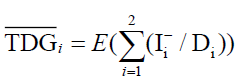14.

(14)

This is the Average Global Des-service Rate. From the analysis in Table 6, we note that the Average Global Des-service Rate has a strong relationship with the change in periodicity and it increases beyond k=4, and becomes in the form of an increasing curve.

Table 6 Determination of Average Global Desservice Rate
k	Without trans-shipment	Complete Pooling	Partial-Pooling
			Twice the Demand	Next Demand	Security Stock=30% of PSiT
2	0.5	0.36	0.34	0.12	0.06
3	0.6	0.46	0.432	0.097	0.05
4	0.45	0.159	0.148	0.053	0.032
5	0.67	0.357	0.351	0.157	0.067
6	0.75	0.465	0.457	0.195	0.09
7	0.865	0.525	0.512	0.293	0.12
8	0.925	0.62	0.602	0.387	0.202
9	1.005	0.77	0.72	0.492	0.297
10	1.121	0.8	0.795	0.537	0.325

But, we analyze the effect of transshipment policies on the minimization of the Average Global Des-service Rate. We notice then that, the first transshipment policy "Complete-Pooling" aims to decrease the rate of the quantity of customer orders not satisfied whatever the periodicity and for example for k=2 this reduction is worth from 0.500 to 0.360 and that the second “Partial-Pooling” policy aims to reduce it as soon as possible and this will be explicit for the last transshipment threshold which equals Security Stock=30% of PSiT.

We then note that the collaboration between two sites 1 and 2 increases the probability of cycles without shortages in each warehouse by the quantity of transshipment transferred planned from 2 to 1 and likewise from 1 to 2 for an increase in the quantity to order for the site 1 and for site 2. Which results in the probability of customer satisfaction improves after the application of the transshipment.

We will then conclude that, the level of service in a collaborative network is higher compared to the network of independent sites and this plays a very important role in decreasing the amount of lost order. This implies that the economic performance of the group of employees does not only depend on the characteristics of each isolated site, it also depends on the characteristics of each retailer and its relationship with the other depots that make up the inventory system and especially when the cost of transfer lateral is weak. This conclusion should be taken into account in the training of employee groups.

Conclusion

This paper targets to study the effect of collaboration in emergencies and applying two policy of transshipment named, "Complete-Pooling" and "Partial-Pooling" between two storage sites on the overall average profit of the system centralized and customer Des-service level.

The most important conclusions can be summarized in the following:

1. The sharing of stocks between sites of the same level greatly optimizes the Average Global Profit of the entire system;

2. Collaboration between sites always improves customer Average Global Des-service Rate, i.e. the probability of no-shortage cycles and the probability of customer satisfaction;

3. In general, the positive effect of collaboration is greater when we apply the "partial pooling" policy with a change in the transshipment threshold.

Several extensions of this model that are of particular interest can be considered in future research. For example, the variation in the average and the standard deviation of the random customer demand and the use of the larger network where the number of sites exceeds the two, integrating the distance between the different storage sites located at the same level.

References

Archibald, T. W., Black, D., & Glazebrook, K. D. (2009). An index heuristic for transshipment decisions in multi-location inventory systems based on a pairwise decomposition. European Journal of Operational Research, 192(1), 69-78.

Indexed at, Google Scholar, Crossref

Dehghani, M., & Abbasi, B. (2018). An age-based lateral-transshipment policy for perishable items. International Journal of Production Economics, 198, 93-103.

Google Scholar, Crossref

Derhami, S., Montreuil, B., & Bau, G. (2021). Assessing product availability in omnichannel retail networks in the presence of on-demand inventory transshipment and product substitution. Omega, 102, 102315.

Indexed at, Google Scholar, Crossref

Feng, P., Wu, F., Fung, R. Y., & Jia, T. (2018). Evaluation of two transshipment policies in a two-location decentralized inventory system under partial backordering. Transportation Research Part E: Logistics and Transportation Review, 118, 207-224.

Google Scholar, Crossref

Feng, X., Moon, I., & Ryu, K. (2017). Warehouse capacity sharing via transshipment for an integrated two-echelon supply chain. Transportation Research Part E: Logistics and Transportation Review, 104, 17-35.

Google Scholar, Crossref

Herer, Y. T., Tzur, M., & Yücesan, E. (2002). Transshipments: An emerging inventory recourse to achieve supply chain leagility. International Journal of Production Economics, 80(3), 201-212.

Indexed at, Google Scholar, Crossref

Lee, C., & Park, K. S. (2016). Inventory and transshipment decisions in the rationing game under capacity uncertainty. Omega, 65, 82-97.

Indexed at, Google Scholar, Crossref

Li, X., Sun, L., & Gao, J. (2013). Coordinating preventive lateral transshipment between two locations. Computers & Industrial Engineering, 66(4), 933-943.

Indexed at, Google Scholar, Crossref

Liao, Y., Shen, W., Hu, X., & Yang, S. (2014). Optimal responses to stockouts: Lateral transshipment versus emergency order policies. Omega, 49, 79-92.

Indexed at, Google Scholar, Crossref

Nakandala, D., Lau, H., & Shum, P. K. (2017). A lateral transshipment model for perishable inventory management. International Journal of Production Research, 55(18), 5341-5354.

Indexed at, Google Scholar, Crossref

Noham, R., & Tzur, M. (2014). The single and multi-item transshipment problem with fixed transshipment costs. Naval Research Logistics (NRL), 61(8), 637-664.

Indexed at, Google Scholar, Crossref

Olsson, F. (2015). Emergency lateral transshipments in a two-location inventory system with positive transshipment leadtimes. European Journal of Operational Research, 242(2), 424-433.

Indexed at, Google Scholar, Crossref

Paterson, C., Teunter, R., & Glazebrook, K. (2012). Enhanced lateral transshipments in a multi-location inventory system. European Journal of Operational Research, 221(2), 317-327.

Google Scholar, Crossref

Silbermayr, L., Jammernegg, W., & Kischka, P. (2017). Inventory pooling with environmental constraints using copulas. European Journal of Operational Research, 263(2), 479-492.

Indexed at, Google Scholar, Crossref

Timajchi, A., Al-e-Hashem, S.M.M., & Rekik, Y. (2019). Inventory routing problem for hazardous and deteriorating items in the presence of accident risk with transshipment option. International Journal of Production Economics, 209, 302-315.

Indexed at, Google Scholar, Crossref

Torabi, S.A., Hassini, E., & Jeihoonian, M. (2015). Fulfillment source allocation, inventory transshipment, and customer order transfer in e-tailing. Transportation Research Part E: Logistics and Transportation Review, 79, 128-144.

Indexed at, Google Scholar, Crossref

Van Houtum, G.J., & Zijm, W.H. (2000). On the relationship between cost and service models for general inventory systems. Statistica Neerlandica, 54(2), 127-147.

Indexed at, Google Scholar, Crossref

Wong, H., Cattrysse, D., & Van Oudheusden, D. (2005). Inventory pooling of repairable spare parts with non-zero lateral transshipment time and delayed lateral transshipments. European Journal of Operational Research, 165(1), 207-218.

Indexed at, Google Scholar, Crossref

Yong, D. (2009, July). Service Parts Inventory Pooling Based on Periodic Review Model. In 2009 IITA International Conference on Services Science, Management and Engineering (pp. 140-143). IEEE.

Indexed at, Google Scholar, Crossref

Received: 05-Dec-2021, Manuscript No. AJEE-21-10248; Editor assigned: 08-Dec-2021, PreQC No. AJEE-21-10248(PQ); Reviewed: 01-Feb-2022, QC No. AJEE-21-10248; Published: 10-Feb-2022