Keywords

Revenue Sharing Contract, Supply Chain players, Game Theory, Transfer Cost Rate, Revenue Sharing Ratio, Stackelberg Leader.

Introduction

As organisations, they work in a typical supply chain network, as each one acts as a clientele when it supplies suppliers 'materials and acts as a supplier while providing its own customers' materials, A supply chain consists of a set of activities and associations promoting (tangible or intangible) the transfer of goods (Cachon, & Lariviere, 2005). It is also important for a variety of facilitators, procedures, activities and information systems to describe the movement of resources, products and knowledge through the path from initial suppliers to final users (Goyat et al., 2019). To incorporate and organize products, knowledge and financial flows across a supply chain, a comprehensive management approach is required. A supply chain may be described as "a network where manufacturers, manufacturing firms, distributors and retailers are supplied and information flows in both directions downstream from manufacturers to customers" (Bhuniya, et al. 2023). In other words, it is the network of producers, wholesalers, retailers and distributors that make raw materials finished and supply goods to customers (Chauhan, & Singh, (2018). The goal is to improve trust and collaboration between supply chain partners and thus increase inventory visibility and inventory speed.

They use some techniques to improve the supply chain, to lower the cost of products as much as possible to attract customers and to get maximum profit. The flows of the supply chain can also be divided into following three primary flows:

Product Flow: transferring products to a consumer through producer including any refunds and service requests from consumers (Cole et al., 2019).

The flow of information: The flow of information involves updating order and the status of the delivery (Council of Supply Chain Management Professionals, 2013).

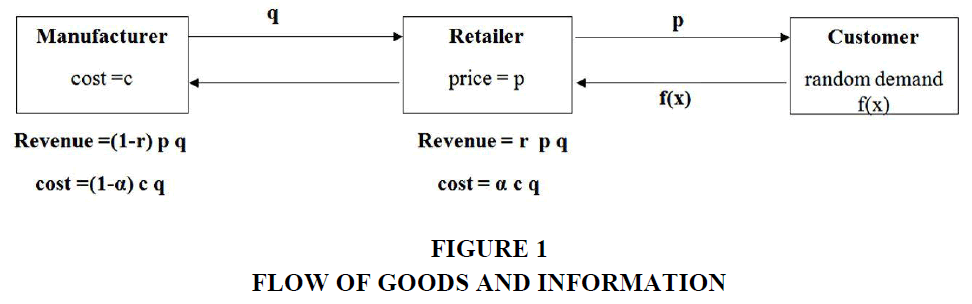
Financial Flows: It includes all the financial details Figure 1.

Supply Chain Contracts

A contract for the supply chain is a system that officially governs transactions between supply chain players (Chauhan, & Singh, (2018). By changing contractual criteria, we can facilitate collaboration and share between vendors, retailers and other actors in the supply chain. The following targets will be met, therefore, by using the contract in SC: to optimize the decentralized SC overall benefit as near as possible to the benefit of the centralized; to ensure that all supply chain operators gain more income than would they have without the agreement.

Perhaps the supplies chain agreements may also serve as a tool to enable various parties in the supply chain to achieve worldwide productivity as well as function as a binding framework for trade terms (Vasnani, 2019). Supply agreements may be used to organize or match the various parties 'objectives to the supply chain's central purpose.

Since few some decades, many researchers have been working on a Game Theoretic approach to model revenue-sharing contracts Cole, et al. (2019). Hence in this project, authors have tried to analyze revenue sharing contract to better coordination between different echelons of the supply chain using a Game Theoretic approach Cole, et al. (2019).

Literature Review

Through literature, researchers have attempted to explore the issue of sharing cost savings with a supplier, a dealer and a retailer by knowledge sharing in both two-tier and three-level supply chain Cao, et al. (2023). They (researchers) use the principle of cooperative game theory to find a particular allocation scheme. First, the estimated cost of the product is measured analytically and then simulated for the manufacturer and the retailer. Then, they create a characteristic-functioning three-person cooperative game and provide conditions required for the unity of all five potential coalitions Erhun, & Keskinocak (2003). They also implemented different allocation To differentiate between two or three members of the supply chain (Erhun, & Keskinocak, (2003).

Hence coordination in the supply chain is necessary. For this different model of SC contracts have been developed. Supply Chain Collaboration represents the commitment between/among supply chain participants which include sharing of benefits, rewards and risks along with the sharing of information. Now there are some contracts have been developed like Emtehani, et al. (2023).

1. Quantity Flexibility (QF) Contracts (Tsay, 1999)

2. Backup Agreements (Eppen and Iyer, 1997)

3. Buy Back or Return Policies (Emmons and Gilbert, 1998)

4. Incentive Mechanisms (Lee and Whang, 1999)

5. Revenue Sharing (RS) Contracts (Cachon and Lariviere, 2000)

6. Allocation Rules (Cachon and Lariviere, 1999)

7. Quantity Discounts (Weng, 1995)

As authors have discussed above that there are so many contracts are available for supply chain coordination, but all are useful for a particular purpose only. So in this thesis, authors are not going in detail of all these contracts, authors will focus our study only on Revenue Sharing Contracts Fallah et al. (2015). But the sharing of revenue creates a great problem in the supply chain. Indeed, as more parties/players enter the market, the profit margins of retailers and suppliers become less and less Fallah et al., (2015). Following this rivalry, the market would usually increase and then remain incomplete, due to lack of contact and cooperation. The consumer would then switch brands/stores typically as price rises. That’s why the revenue of all parties (who are involved in the supply chain) is inter-related Fallah et al. (2015).

It is known that every party (i.e., retailer, wholesaler and manufacturer) wants to maximize their profit and nobody want to collaborate because it decreases individual profit and efficiency of the supply chain, but simultaneously increases total supply chain profit. Hence Supply chain contracts are such mechanisms aimed at coordinating decentralized supply chain through the fulfilment of two objectives:

Increasing supply chain’s profit comparable to that achieved through the centralized supply chain, and Risk-sharing among various coordinating partners Giannoccaro & Pontrandolfo, (2004). Hence collaboration is necessary so that all parties could get equal profit and they can get a good hold over the whole market. This collaboration among parties will decide all prices i.e. retailer price and the wholesale price which decide the profit margins, inventory etc for higher revenues Gupta & Barua, (2017). Game theory can be used for finding a good solution via revenue-sharing contracts. That’s why nowadays most persons are using it, to optimize the supply chain, understand and help parties to make the right decisions at the right time (Nagarajan & Sošić, 2008). Hence two types of game-theoretic models have been given, first cooperative and second non-cooperative, which depends on how the involved parties are behaving. In non-cooperative games, two types of concepts are being used first Nash equilibrium and second is Stackelberg equilibrium (Gupa & Barua, 2017).

In every game-theoretic model, some keywords are commonly used, like strategy, action, payoff etc. For getting the best payoff, players have to choose an action in available strategy Gupta, & Barua (2017). If players choose their strategy simultaneously, it is called to Nash Equilibrium and when players choose their strategies one after other, it called Stackelberg Game. A seller sells the products of a supplier at a wholesale price rate lower than the market-marginal price in a revenue-sharing arrangement. Now it can be optimized through Game Theory approach. Hence authors can see this revenue-sharing contract as a Stackelberg game and find Nash equilibrium.

The contract must be decided by the players to influence the decision. The played player acts as a leader of Stackelberg here, and the player who selects the decision variable value optimally according to the contract ultimately acts as a successor of Stackelberg. Hence in Stackelberg game, there are two types of games are available for any party first, Stackelberg leader game, second Stackelberg follower game (Gupta & Barua, 2017). Let us assume that the role of Stackelberg leader will be played by the manufacturer and Stackelberg follower (retailer) decides the ordered quantity. The opposite will happen if the retailer plays first (called as Stackelberg leader) and then the manufacturer (called as Stackelberg follower) decides later on Gupta, & Barua, (2017).

In co-operative theory, the player looks directly at the potential results, how can the other player achieve them, what coalitions can form and how they can create a better payout? Thus, the theory of cooperative games offers numerous recipes for this method. The interaction between the players is such a significant application (Hou, et al. 2017). Generally, there are two types of controls have been used in SCM, first is centralized control and second is decentralized control. Central control is available for the Supply Chain only to a single Decision Maker who manages the whole supply chain and who should have all the relevant knowledge about the whole SC. Central control guarantees the reliability of the network (channel coordination). At the other hand, many decision-makers are available under decentralized control and each player can make his own choices (Hou, et al. (2017).

Therefore, alternate arrangements that manage the supply chain must be taken into account. In general, in (coordinating) contracts, the following aspects are relevant which includes Profitability, Fairness, flexibility and Implement ability (Hou, et al. (2017). The central optimization approach, however, is just an alternative to the real supply chain structure; because most supply chain systems are decentralized. There are three problems with the central optimization models:

Independence of members of the supply chain is overlooked in central SCM and competition between members that reduce the efficiency of the supply chain.

The costs of processing information shall be high, as the central decision-maker must obtain all information from each member of the supply chain and eventually provide the members with instructions.

Central optimization models efficiency. However, it might not be possible to model and calculate the problem if it is very broad and difficult (Hou, et al. (2017).

There are many self-interested members/companies in the inter-organizational cooperation supply chain. All players are willing to cooperate for supply chain performance, and therefore need the cooperation or contract process which has to be negotiated and established carefully. Competition between players has been shown to lower and not optimal machine performance. And what is the issue of whether the supply chain participants should be coordinated? To carry out this function, a contract-based negotiation process will be used and the contract must meet the following rules:

The player's benefit must be assured before cooperation in the supply chain not below the amount of profits and the overall cooperative income-participatory cap shall be reasonably shared by the player.

Any opportunities to deviate from the optimal solution of a system-Consistent constraint should be minimized Pakseresht, et al. (2020).

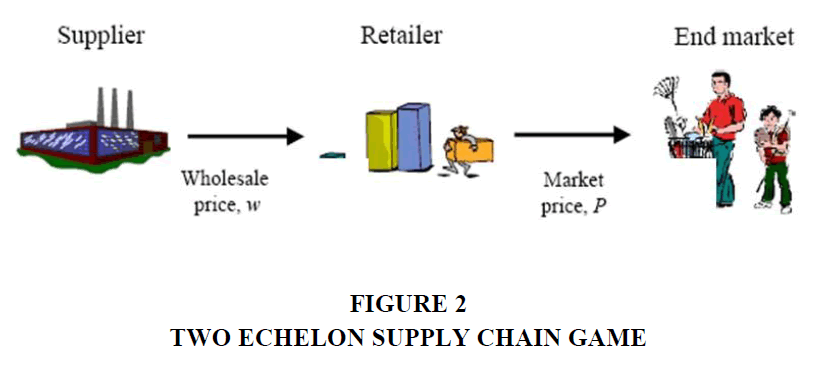
Two-stage supply chain problem without revenue sharing contract Figure 2.

As we all know, all parties involved in fulfilling a consumer requirement have a supply chain, directly or indirectly. In SC, we generally call parties who involve in it like manufacturer, distributor and retailer. If there are two parties (i.e., manufacturer and retailer) are involved, then we call it two-stage supply chain and if three parties (i.e., manufacturer, distributor and retailer) are there, then we call it three-stage supply chain.

Two-stage Supply Chain Management with facing problems (by manufacturer and retailer):

1. The management of product movement and information flows between manufacturers and retailers can be established to satisfy the demands of the consumer.

2. It includes material procurement processes, storage, physical distribution procurement, acquisition and management of information.

3. The supply chain is, in other words, the process of shipment of goods by the consumer through the raw materials step, the production, manufacture and distribution.

4. SCM needs to work closely to manage order production, order take-up and delivery by a supplier and retailer.

5. For maintaining proper distribution, every party has to find the right ordering policy which is totally on varying demand and lead time of supplier party also.

6. The other goal of an efficient framework for the management of the supply chain is to reduce stocks, taking into account that goods are available when necessary. This ensures that the manufacturer is appropriate for the retailer to buy.

7. Hence, we can divide the SCM flows into basic flows i.e., Product, information flow and Financial flow

8. So, sharing of information is necessary to all parties which ensure them to available the product at an exact time with reducing cost. This helps them to easily manage their resources so that they can fulfil future demand also.

Actual Process in the Two-Stage Supply Chain

As previously mentioned, a supply chain includes trading partners linked to financial, information and product/service flows. Efficient management is necessary to satisfy customers request and to maximize their benefit to ensure that a good relationship between supplier and retailer is preserved. Yet it doesn't usually occur. Now authors continue with a two-stage simple supply chain model involving two parties (i.e., produce and retailer). In the model, the seller is selling his product, which sets the retail price and markets the commodity to customers. But they don't want to share the details, because both parties (manufacturer and retailer) want to increase their profits themselves. The outcomes are all less profitable, unsatisfied customers and so on. The Supply Chain cycle starts with a customer order, followed by manufacturing, storage and distribution of goods, and ends finally with customer distribution. That all can happen through an information service network which includes Processing customer orders, inventory, scheduling, transport, storage, and customer support (Supply Chain Management Review, 2017).

Yet when these things are handled correctly, the biggest issue is that. As the authors discussed previously, efficient management of the supply chain would be advantageous if it creates decreased inventories, lesser operational expenses and end-customer expectations. Both stakeholders need long-term consideration and short-term decisions (day-to-day operations) to address both problems. Strategic decisions are driven by long-term corporate policy decisions which take account of nature which function of the entire supply chain. Operational actions on the other hand deal with a company's everyday operations and issues.

Thus, the authors are distributing the supply chain into the following three elements:

1. Production/Manufacturing

2. Inventory

3. Information

Production/Manufacturing: The researchers are coming up with strategic decisions (regarding production), then the manufacturer would identify the customer’s expectation. Hence strategy needs to use to ensure that how many portions can be produced in-house and how much from out-source. All decisions need to take while keeping in probabilistic demand (Pakseresht, M., Mahdavi, I., Shirazi, B., & Mahdavi-Amiri, N. (2020)). Irrespective of that work schedule, maintenance and various other meetings need to schedule to meet all requirements to ensure timely quality production.

Inventory

In the two-stage supply chain, both manufacturer and retailer should have to maintain its inventory level. Because an accurate inventory level can easily manage/fulfil the varying demand. But inaccurate and excess inventory level also increases product cost. Hence, every party has to decide when to order? That is called the reorder point. Hence it is necessary to keep in the record that what quantity is to be required in the next period. For this, every party has to know the exact/calculated demand of lower party (Jandl, C., Wagner, M., Moser, T., & Schlund, S. (2021). This process needs the information sharing between parties and information sharing contract is to be needed.

Information

As authors discussed earlier that an effective supply chain management requires the right information to make the right decision at the right time, which reduces the bullwhip effect. Hence sharing of information is a must (Jandl, C., Wagner, M., Moser, T., & Schlund, S. (2021) Problem formulation: Considering the earlier points a two-stage supply chain will generally face the following problems:

What quantity should retailer order?

If anyone goes into deep, it can easily find out the retailer problem, is related to the quantity to be ordered. As authors all know that demand is probabilistic, not deterministic (generally).

What quantity should the manufacturer produce?

The same problem has to face manufacturer also because he knows that retailer can place any quantity (because of probabilistic demand).

To overcome this problem both manufacturer and retailer have to see their inventory stock. According to this, they both have to forecast demand. Along with retailer should know the lead time of quantity ordered through manufacturer and manufacturer should know that in how much time he can produce that quantity ordered.

Ordering Policy: As the authors discussed in the earlier section, that everything depends on ordering policy. Many parties are using different techniques which depend on the demand pattern and lead time of getting quantity. authors are discussing two ordering policies.

(s, S) policy: If demand is probabilistic, then parties generally use this ordering policy. In which they have to maintain S (pre-defined level) keeping in mind s (inventory safety stock). Whenever the retailer sees that an inventory stock falls below safety stock (s), he issues an order to manufacturer up to S (pre-defined level).

Optimal order policy: If demand is deterministic, then parties use this ordering policy using dynamic programming.

Bullwhip effect: As authors have already discussed that demand is probabilistic and no party want to suffer the loss that’s why they generate different order from actual demand. The volatility of the market increases as the supply chain shifts away from the consumer and small shifts in customer demand can lead to significant upstream order changes. The Bullwhip effect was named this phenomenon. Here authors are taking two-stage supply chain which consists of a manufacturer and a retailer. In which the manufacturer gets the raw material from the supplier, who then turn raw material into finished goods and supplies these finished goods to the retailer. Finally, the retailer transfers these goods to customers and fulfils their demand (Singh and Rathi, 2019).

According to Rezayat, et al. (2020), in the real process of two-stage SCM retailer gets the demand from the customer, according to that demand retailer give the order to manufacturer and manufacturer has to supply that given order to the retailer. Here two cases can be taken, first when the manufacturer has enough supply to fulfil retailer’s order, second when the manufacturer doesn’t have enough quantity to fulfil retailer’s order. If any player (i.e., either manufacturer or retailer) doesn’t fulfil the demand of lower party then he will be in loss and anyhow he has to fulfil that backorder. Hence, they have to pay some backorder cost.

Variable description:

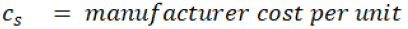
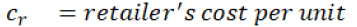
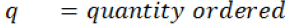
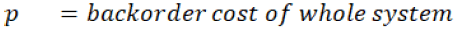
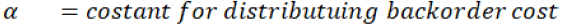
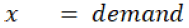
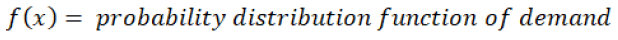
Terms Used

Transfer cost rate: It is the cost rate, which is transferred to the retailer by the supplier under contract.

Revenue sharing ratio: It is denoted by r and the value lie between 0 and 1. Under the Revenue Sharing contract, the retailer has to share some revenue with the supplier. Because the supplier has already reduced the wholesale price, so they make a contract that whatever revenue will generate by the retailer, he has to share some ratio (r) of his revenue to the supplier.

Salvage value: It is the unit cost of the item which has remained unsold and afterwards sells as scrap.

In any SCM demand can be deterministic or probabilistic. If demand is deterministic then retailer does not change his order quantity according to time. But if demand is probabilistic then it leads to information sharing. As authors know that every party wants to maximize his profit, so if they change their quantity according to demand and decides not to share that information to another party. Hence the phenomenon of bullwhip effect occurs.

If authors assume that manufacturer fulfil all orders which he gets from the retailer, then the manufacturer’s cost will be c_s * q and retailer’s cost will be c_r * q.

If they are unable to fulfil the demand, they have to incur backorder cost (p). Hence αp cost will be added to the retailer and (1-α) p will be added to the manufacturer. Then the cost of both players will be given by the following expression:

The total cost of the manufacturer:

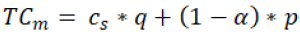(1)

Similarly, the total cost of the retailer is:

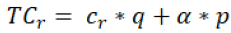(2)

Both players aim to minimize their cost.

For manufacturer

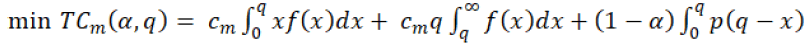(3)

For retailer

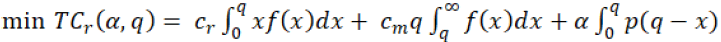(4)

In the Equation 1 to 4, the authors have not added any other factor/cost, but in fact, there are so many other factors/costs are also considered which are directly-indirectly involve in the system like lead times, inventory holding costs etc. authors will add these factors later on.

Introduction to Revenue Sharing contract

Before going to any detail about revenue sharing contract, first of all, authors will see that what exactly revenue sharing is and why it is needed in the supply chain?

What Is Revenue Sharing Contract?

If all supply chain players operate in collaboration, they can both increase their income and social benefits as well. The two parameters that characterize the profit-sharing arrangement (mode, α); in exchange for a percentage (1- α) of the retailer's profit on the selling product, the manufacturer pays a market price unit number, lower than unit cost c. In return. The company retains α portion of its profits. The decentralized supply chain will be organized under this revenue-sharing arrangement, which involves a centralized supply chain involving one manufacturer and one seller. It is not likely that the retailer does not have enough cash to purchase all the goods that the supplier needs and a retailer may miss many sales opportunities and losses does lead to losses for the supplier. If goods are unvented at the end of the period of the sale, the distributor will sell the remaining at the rescued price; on the opposite, the distributor would have goodwill losses, if the order can't meet the business demand (Rezayat, et al. (2020).

In this contract whatever revenue retailer gets, he has to share some ratio of that revenue to manufacturer also, is called Revenue Sharing Contract. Generally, in this contract manufacturer sells his product less than the original wholesale price because he has already made an RS contract to the retailer so that after selling the product to the customer what revenue he gets, he has to share some ration of that revenue to manufacturer also. So that manufacturer can also get remaining revenue which he has been losing by reducing his wholesale price. Similarly, the retailer can also purchase more products because of the less wholesale price. One thing is to be remembered that this contract will be valid in both cases whether the retailer is in profit or loss. This RS contract can be applied to salvage revenue.

Comparison of Revenue Sharing Contract with Simple Supply Chain

Authors know that contract is needed for maximization the players’ profit, hence authors are discussing one of the contracts (i.e., revenues sharing contract) which can be used for coordination. In this contract authors added two more parameters, first is revenue sharing ratio (r) and second is transfer ratio cost (α). Other parameters are the price of the unit product (q), cost of the unit product (c) and demand distribution f(x). In this RS contract, the manufacturer reduces the wholesale price and takes some part of the revenue of sold items from the retailer. Because the wholesale price is reduced, the retailer can purchase more items to minimize the risk. In other words, the retailer will be in less profit after getting salvage revenue, because he purchased items in reduced wholesale price.

Assume that the manufacturer has a production cost p, charges a wholesale price of c, and shares a fraction r of the retailer’s revenue. The retailer charges a retail price p and can salvage any leftover units for s.

The optimal order quantity Q* ordered by the retailer is evaluated by equation 5 and 6.

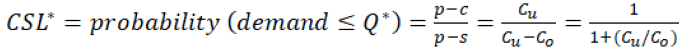(5)

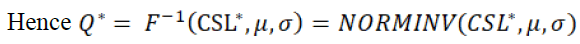(6)

In our case CSL* are shown in equation 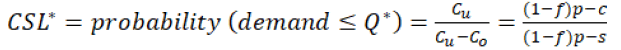7.

(7)

For better understanding authors take an example, in which manufacturer sell the product to the retailer at Rs. 10/- and retailer sell it to the customer at a wholesale price of Rs. 200/-. Along with retailer shares half of this revenue with the manufacturer (i.e., authors take revenue ratio r = 0.5). The distribution of demand is considered to average with mean μ = 1000 and standard deviation with σ = 300.

Hence the manufacturer’s profit is estimated with the help of equation 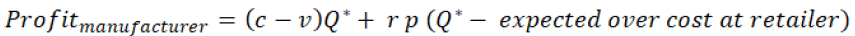8.

(8)

Similarly, the retailer’s profit is estimated with the help of equation 9 and 10.

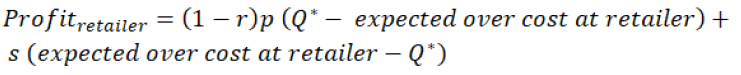(9)

where

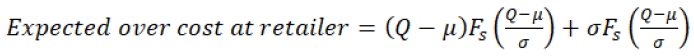(10)

Example: authors got the following result for r = 0.5

Expected overstock = 399

Expected manufacturer profit = 84660/-

Expected retailers’ profit = 98580/-

Expected supply chain profit = 183315/-

And without a revenue-sharing contract,

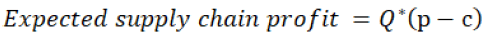
= 10000 (200-10)

= 190000/-

Revenue Sharing Contract and its Advantages

Similarly, to other contracts, this RS contract has also some advantages. Now authors will take a look some of them.

Risk-neutral: This contract makes all parties risk neutral because no party is willing to suffer losses in revenue. The main reason behind this is that every party has to share ratio of its revenue. It doesn’t matter whether revenue comes from selling units or from salvage units.

Flexibility for the buyer: Because every party is well known before ordering that it would not have to bear the whole burden itself. So, it can change its ordering quantity according to conditions.

An equal share of revenue: Here equal means not equal but some ratio have to share each party which make some limitations (as authors mentioned earlier).

Minimizing unsatisfied customers: As there is no risk remaining to order the quantity, the buyer can make more order to satisfy the customers if demand changes. This leads to a smaller number of unsatisfied customers.

Increase efficiency of Supply Chain: As authors discussed earlier that in this RS contract, information has to be shared between parties which reduces the bullwhip effect and hence increases the efficiency of Supply Chain.

Model Formulation

Formulation of a game of two-stage supply chain without RS contract, now consider a two-echelon Supply Chain game which includes one supplier and one retailer and retailer and customer as shown in the Figure 3.

A game-theoretic model set up: Authors must know the following things before setting up a game theory model:

The participating teams: Game rules that describe the sequence of moves, as well as the possible acts and details each player has to provide while moving. The outcome of the game for any action possible.

Compensation based on outcomes (expected).

Hence authors are using following game theory notations for making this as a Supply Chain game. Here authors consider this as normal form game, which includes:

Players (i = 1,2,.....,n)

Strategies available to each

player and

Payoffs 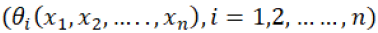received by each player.

Each strategy is set 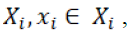so authors call the Cartesian product 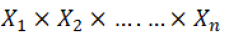the strategy space (typically the strategy space is Rn). Nonetheless, every player with a set of feasible strategies in simultaneous moving games depends on the other players 'strategies.

Model formulation Sharma, (2019):

Authors assume that the degree of demand provided by the distributor is randomly distributed following an interval of [a, b)(a<0) with a corresponding c.d.f. F(x) and the continuous p.d.f. f(x). In the RSC model authors took

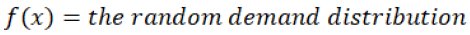
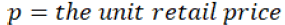
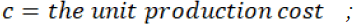
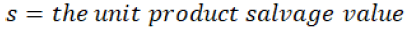
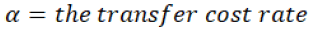
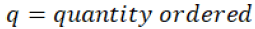
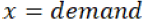
As authors all know that in any supply chain every player wants to make his profit maximum. Hence the decisions generally conflict. To minimize these conflicts and maximize the profit, the contract is necessary. As authors discussed that supply chain management is divided into two types, first centralised and second decentralised.

In centralised decision SCM, only one single decision-maker is there, who takes all decisions and control the whole SCM through his decisions. He is the only responsible to take all risks. In another case (decentralised SCM), the decision is together decided by all parties. But generally, it seems that profit is always more in centralised SCM case comparatively decentralised SCM case. Hence the expected channel profit B (q) for centralised SCM, which can be expressed by equation 11 (for whole supply chain):

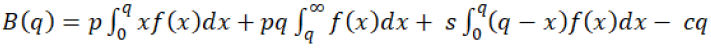(11)

where the transfer and revenue-sharing elements are not involved. It can be derived from the optimality conditions as shown in equation 12, that the optimal quantity q* to be delivered must satisfy,

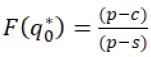(12)

Proof: authors can easily find out the optimal quantity q*, by differentiating the profit equation 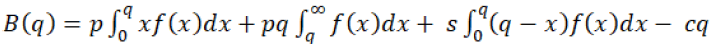13:

(13)

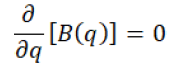
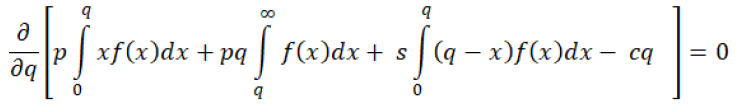
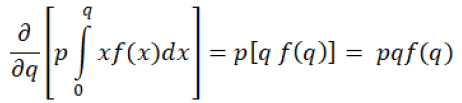
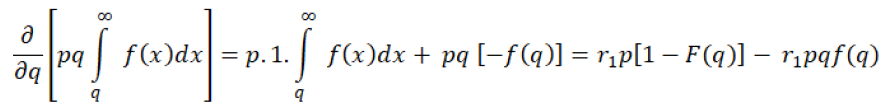
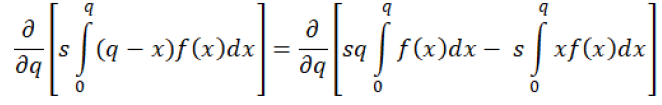
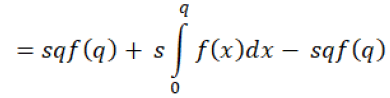
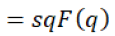
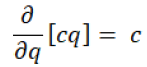
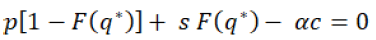
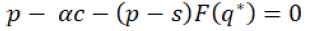
By combining all equations, we have got equation 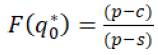14.

(14)

Formulation of a game of two-stage supply chain with RS contract

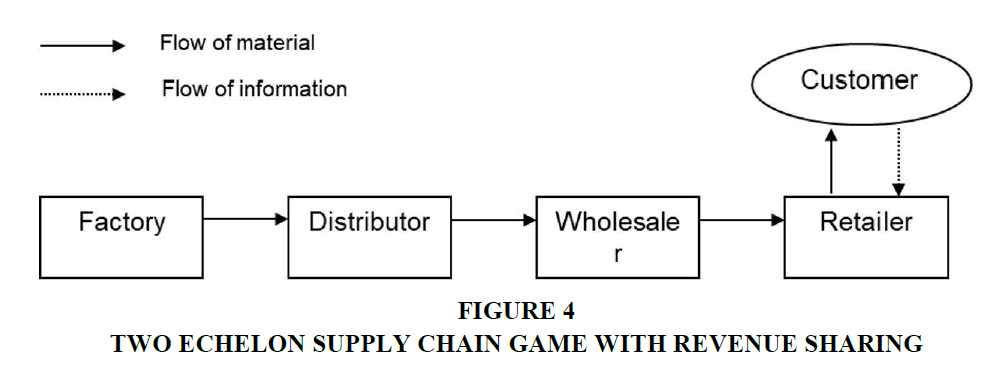
Sharma, (2019) describes this revenue-sharing contract into two types which authors will take later on. In which the retailer caters to the market demand, D(p) that is uncertain and characterized by the cumulative distribution function Figure 4.

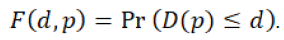
Authors have also used Stackelberg to formulate the question as suggested that one player would lead the game and the other follows the game. He assumes that the income sharing rate r is fixed for the sharing of revenue; i.e., it should be predefined. The supplier's Stackelberg game leader is the retailer's α transfer rate, and then the retailer calculates the amount of q to be ordered from the supplier; when the Stackelberg game leader is the retailer, he decides α on the shipping cost rate and the supplier decides q on the amount to be delivered to the retailer. The retailer's Stackelberg game is the Stackelberg game lead took the following two cases in that revenue sharing contract:

The supplier and retailer are not sharing salvage revenue (SRNS).

The supplier and retailer are sharing salvage revenue (SRS).

In these two cases with one supplier and one retailer, two factors are important like the revenue-sharing rate (r) and transfer cost rate (α) for finding profits of the retailer, supplier and the supply chain (Singh, et al. (2019).

When the Salvage Revenue is Not Shared Zhaoqiong Qin 2008

According to, there will be two cases, one when profit is shared but salvage revenue is not shared and another when salvage revenue is also shared. authors will take both cases one by one.

Case I: Supplier is Stackelberg leader and retailer is the follower: In this case, authors assume that supplier play first and then after seeing the supplier’s strategy/action, the retailer chooses his best action to maximize his profit. Here authors are taking this game as a Stackelberg leader-follower game; in this situation, the supplier will be known as Stackelberg leader and retailer will to be known as Stackelberg follower. Every player will change his strategy/action and find his best option to get maximum profit until they get their optimal profit.

Hence in this RS contract, supplier (who is a Stackelberg leader) starts the game and chooses the α (transfer cost) and retailer (who is a Stackelberg follower) decides the q (quantity ordered). In this case retailer orders, the quantities according to customers’ demand and supplier arrange that order according to the retailer’s order. Then the manufacturer decides transfer cost and at last, the retailer delivers quantities to customers. After delivering retailer keeps some ratio of that revenue and returns remaining to the supplier as per RS contract. Both supplier and retailer are sharing the revenue so the retailer’s expected profit will be given by the equation 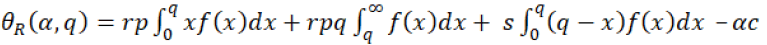15.

(15)

In the equation 15, the first expression shows the ratio of revenue when retailer orders q quantity and demand is less than q, similarly the second expression shows the ratio of revenue when he orders q quantity and demand is also more than q. The third expression shows the salvage revenue and last fourth one expression shows the cost of the retailer. Hence the optimal profit will be given by the equation 16 in which, the retailer chooses optimal order quantity q* to maximize his profit:

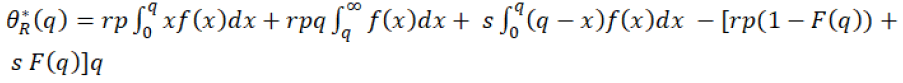(16)

Similarly, the supplier’s expected profit will be given by the equation 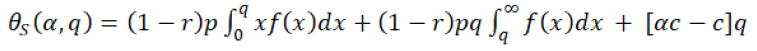17:

(17)

In the equation 17, the first expression shows the ratio of revenue of supplier which he gets from the retailer as per revenue-sharing contract, when retailer orders q quantity and demand is less than q, similarly the second expression shows the ratio of revenue of supplier which he gets from the retailer as per revenue-sharing contract when retailer orders q quantity and demand is also more than q. The last expression shows the cost of the supplier.

Suppose supplier chooses α = α_R* (q) in which supplier considers the retailer’s optimal order quantity q* to maximize his profit, then the expected profit of supplier will be 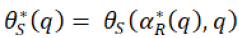which will be given by the equation 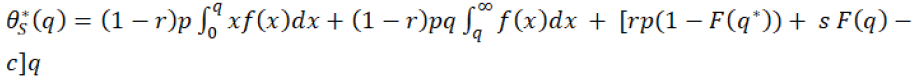18:

(18)

For getting the maximum profit equation 19 should also be satisfied with optimal profit:

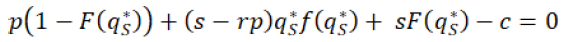(19)

Case II: Retailer is Stackelberg leader and the supplier is a follower

In this case, authors assume that retailer play first and then after seeing the retailer’s strategy/action, the supplier chooses his best action to maximize his profit. Here authors are taking this game as a Stackelberg leader-follower game; hence in this situation retailer will be known as Stackelberg leader and supplier will be known as Stackelberg follower. Every player will change his strategy/action and find his best option to get maximum profit until they get optimal profit.

Hence in this RS contract, retailer (who is a Stackelberg leader) starts the game and chooses the α (transfer cost) and supplier (who is a Stackelberg follower) decides the q (quantity ordered). In this case retailer orders, the quantities according to customers’ demand and supplier arrange that order according to the retailer’s order.

Then retailer decides the transfer cost (act as a Stackelberg leader) and supplier (act as a Stackelberg follower) decides the ordered quantity, at last retailer, delivers quantities to customers. After delivering retailer keeps some ratio of that revenue and returns remaining to the supplier as per RS contract.

Both supplier and retailer are sharing the revenue, So supplier’s expected profit will be given by the equation 20:

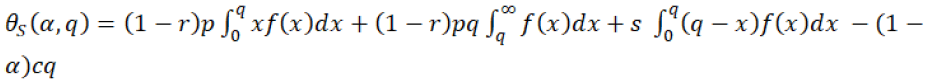(20)

In the equation 20, the first expression shows the ratio of revenue of supplier which he gets from the retailer as per revenue-sharing contract, when retailer orders q quantity and demand is less than q, similarly the second expression shows the ratio of revenue of supplier which he gets from the retailer as per revenue-sharing contract when retailer orders q quantity and demand is also more than q. The third expression shows the salvage revenue of supplier and the last fourth one expression shows the cost of the supplier.

Hence the optimal profit will be given by the equation 21 in which, the supplier chooses optimal order quantity q* to maximize his profit,

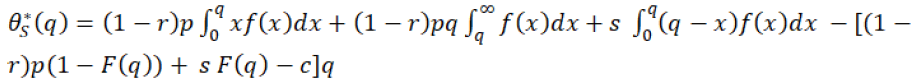(21)

Similarly, the retailer’s expected profit will be given by the equation 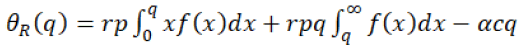22:

(22)

In the equation 22, the first expression shows the revenue when retailer orders q quantity and demand is less than q, similarly the second expression shows the revenue when he orders q quantity and demand is also more than q. The last expression shows the cost of the retailer.

Hence the optimal profit will be given by the following expression in which, retailer considers supplier’s optimal order quantity q* to maximize his profit, where retailer chooses the 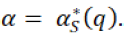So the expected profit 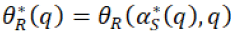will be given by the equation 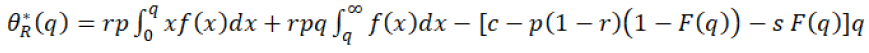23.

(23)

For getting the maximum profit equation 24 should also satisfy,

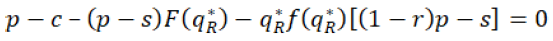(24)

4. Result and Discussion

For more understanding authors use one numerical example, in which authors use the following notation and values:

f(x) = the uniform distribution with range [400, 10000]

p = the unit retail price = Rs. 12/-

c = the unit production cost = Rs. 10/-

s = the unit product salvage value; = Rs. 2.8/-

α = the transfer cost rate

r = revenue sharing ratio for sold quantity

When the salvage revenue is also shared but assuming different revenue ratio i.e., revenue sharing ratio for sold quantity and revenue sharing ratio for salvage value, so authors get the following result like:

For r = 0.4

authors get optimal quantity for supplier = 2042.86

Optimal quantity for retailer = 1682.35

Similarly, the authors tried this for the various value of revenue ratio and got the following results as shown in Table 1.

Table 1 The Impact of Salvage Revenue on the Optimal Order Quantity, when Salvage Revenue is Not Shared
r1	q*S	q*R
0.4	2042.86	1682.35
0.42	2000.00	1712.57
0.44	1958.90	1743.90
0.46	1919.46	1776.40
0.48	1881.58	1810.13
0.5	1845.16	1845.16
0.52	1810.13	1881.58
0.54	1776.40	1919.46
0.56	1743.90	1958.90
0.58	1712.57	2000.00
0.6	1682.35	2042.86

When the salvage revenue is also shared Singh, et al. (2019).

The case I: Supplier is Stackelberg leader and retailer is a follower: In this case, authors assume that supplier play first and then after seeing the supplier’s strategy/action, the retailer chooses his best action to maximize his profit. Here authors are taking this game as a Stackelberg leader-follower game; hence in this situation supplier will be known as Stackelberg leader and the retailer will be known as Stackelberg follower (Singh, 2016). Every player will change his strategy/action and find his best option to get maximum profit until they get Nash equilibrium.

Hence in this RS contract, supplier (who is a Stackelberg leader) starts the game and chooses the α (transfer cost) and retailer (who is Stackelberg follower) decides the q (quantity ordered). In this case, supplier and retailer are sharing revenue which includes salvage revenue also. So, the retailer’s expected profit will be given by the equation.

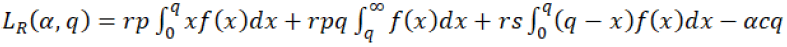(25)

In the equation 25, the first expression shows the ratio of revenue when retailer orders q quantity and demand is less than q, similarly the second expression shows the ratio of revenue when he orders q quantity and demand is also more than q. The third expression shows the ratio of revenue of salvage and the last fourth one expression shows the cost of the retailer.

And optimal profit will be given by the equation 26 in which, the retailer chooses optimal order quantity q* to maximize his profit,

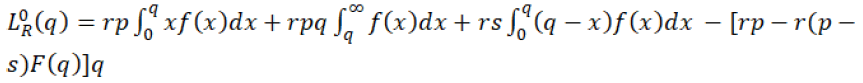(26)

Similarly, the supplier’s expected profit will be given by the equation 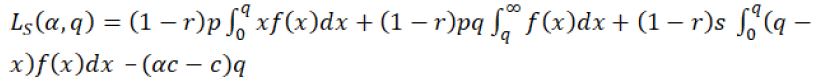27.

(27)

Suppose supplier chooses 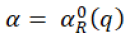in which supplier considers the retailer’s optimal order quantity q* to maximize his profit, then the expected profit of supplier will be 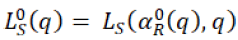and which will be given by the equation 28 in which,

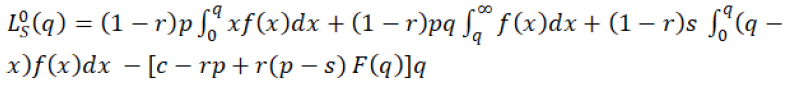(28)

For getting the maximum profit equation 29 should also satisfy,

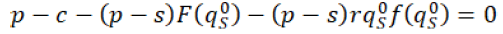(29)

Case II: Retailer is Stackelberg leader and the supplier is a follower: In this case, the authors assume that the retailer plays first and then after seeing the retailer’s strategy/action, the supplier chooses his best action to maximize his profit. Here authors are taking this game as a Stackelberg leader-follower game; hence in this situation retailer will be known as a Stackelberg leader and supplier will be known as a Stackelberg follower. Every player will change his strategy/action and find his best option to get maximum profit until they get Nash equilibrium (Zhang, et al. (2019). Hence in this RS contract, retailer (who is a Stackelberg leader) starts the game and chooses the α (transfer cost) and supplier (who is a Stackelberg follower) decides the q (quantity ordered). In this case, supplier and retailer are sharing revenue which includes salvage revenue also. So, the supplier’s expected profit will be given by the equation 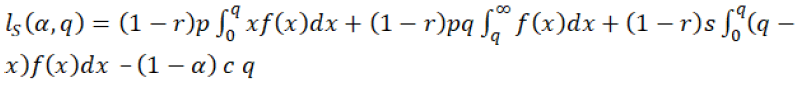30:

(30)

And optimal profit will be given by the equation 31 in which, the supplier chooses optimal order quantity q* to maximize his profit,

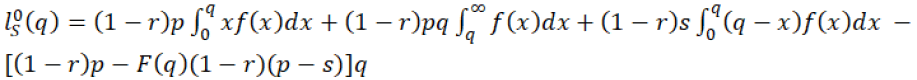(31)

Similarly, the retailer’s expected profit will be given by the equation 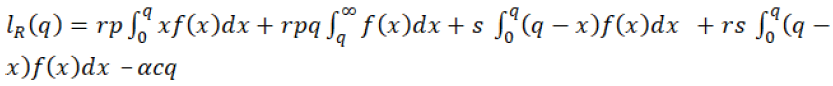32:

(32)

And optimal profit will be given by the equation 33 in which, retailer considers supplier’s optimal order quantity q0 to maximize his profit, where retailer chooses the 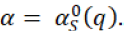So the expected profit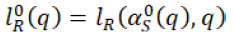

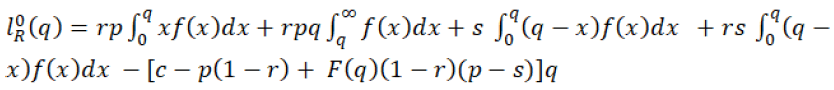(33)

For getting the maximum profit equation 34 should also satisfy,

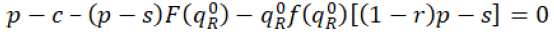(34)

For more understanding authors use one numerical example, in which authors use the following notation and values:

f(x) = the uniform distribution with range [400, 10000]

p = the unit retail price = Rs. 12/-

c = the unit production cost = Rs. 10/-

s = the unit product salvage value ;= Rs. 2.8/-

α = the transfer cost rate

r = revenue sharing ratio for sold quantity

When the salvage revenue is also shared but assuming different revenue ratio i.e., revenue sharing ratio for sold quantity and revenue sharing ratio for salvage value, so authors get the following result like:

For r = 0.4 authors get optimal quantity for supplier = 1776.40

Optimal quantity for retailer = 1554.35

Similarly, the authors tried this for the various value of revenue ratio and got the following results are shown in Table 2.

Table 2 The Impact of Salvage Revenue on the Optimal Order Quantity, when Salvage Revenue is Also Shared
r1	q*S	q*R
0.4	1776.40	1554.35
0.42	1751.38	1574.02
0.44	1727.05	1594.20
0.46	1703.30	1614.91
0.48	1680.38	1636.16
0.5	1657.97	1657.97
0.52	1636.16	1680.38
0.54	1614.91	1703.30
0.56	1594.20	1727.05
0.58	1574.02	1751.38
0.6	1554.35	1776.40

Author Contribution Statement: All the authors have significantly contributed to the development and the writing of this article.

Funding Statement: The study received no financial support from any of the public, private, or non-profit funding bodies.

Disclosure Statement: No potential conflict of interest was reported by the author(s).

Data Availability Statement: Data are contained within the article.

Conclusion

Authors have seen the impact of Revenue sharing contract in the supply chain and authors found that revenue sharing contract is needed to optimize individual profit. For this, authors have tried to find the optimal setting for each player in two cases, i.e., when one is Stackelberg leader and other is Stackelberg follower and vice versa. We also tried to understand this revenue-sharing contract in both cases i.e., horizontal expansion and vertical expansion. At last, authors can conclude that every player can get his maximum profit with chosen optimal setting and revenue ratio that provides confidence in each player to sustain in the market. We collaborated with SC members to create two contracts based on trade credit financing in order to overcome this obstacle. distinct TCF contract conditions were used to offer and evaluate two distinct situations. The manufacturer could wait until the end of the term to make payments in the second scenario, whereas in the first scenario, the suppliers were paid before the end of the period. The relationships amongst the SC members were modelled as multi-leader Stackelberg games with both horizontal and vertical competition in each scenario. In order to maximize their individual earnings, the non-cooperative suppliers (as leaders) play a Nash game to decide on the contract specifications while taking the manufacturer's reaction into account.

References

Bhuniya, S., Pareek, S., & Sarkar, B. (2023). A sustainable game strategic supply chain model with multi-factor dependent demand and mark-up under revenue sharing contract. Complex & Intelligent Systems, 9(2), 2101-2128.

Indexed at, Google Scholar, Cross Ref

Cachon, G. P., & Lariviere, M. A. (2005). Supply chain coordination with revenue-sharing contracts: strengths and limitations. Management science, 51(1), 30-44.

Chauhan, C., & Singh, A. (2018). Modeling green supply chain coordination: current research and future prospects. Benchmarking: An International Journal, 25(9), 3767-3788.

Indexed at, Google Scholar, Cross Ref

Cole, R., Stevenson, M., & Aitken, J. (2019). Blockchain technology: implications for operations and supply chain management. Supply chain management: An international journal, 24(4), 469-483.

Cao, X., Bo, H., Liu, Y., & Liu, X. (2023). Effects of different resource-sharing strategies in cloud manufacturing: A Stackelberg game-based approach. International Journal of Production Research, 61(2), 520-540.

Erhun, F., & Keskinocak, P. (2003). Game theory in business applications. Management Science and Engineering, Stanford University, Stanford.

Emtehani, F., Nahavandi, N., & Rafiei, F.M. (2023). Trade credit financing for supply chain coordination under financial challenges: a multi-leader–follower game approach. Financial Innovation, 9(1), 6.

Fallah Nezhad, M. S., Rasay, H., & Zare Mehrjerdi, Y. (2015). Modeling and numerical analysis of revenue sharing contract based on the Stackelberge game theory. International Journal of Supply and Operations Management, 1(4), 439-465.

Indexed at, Google Scholar

Giannoccaro, I., & Pontrandolfo, P. (2004). Supply chain coordination by revenue sharing contracts. International journal of production economics, 89(2), 131-139.

Gupta, H. and Barua, M.K. (2017), “Gupta, H., & Barua, M. K. (2017). Supplier selection among SMEs on the basis of their green innovation ability using BWM and fuzzy TOPSIS. Journal of cleaner production, 152, 242-258.

Hou, Y., Wei, F., Li, S. X., Huang, Z., & Ashley, A. (2017). Coordination and performance analysis for a three-echelon supply chain with a revenue sharing contract. International Journal of Production Research, 55(1), 202-227.

Pakseresht, M., Mahdavi, I., Shirazi, B., & Mahdavi-Amiri, N. (2020). Co-reconfiguration of product family and supply chain using leader–follower Stackelberg game theory: Bi-level multi-objective optimization. Applied Soft Computing, 91, 106203.

Indexed at, Google Scholar, Cross Ref

Jandl, C., Wagner, M., Moser, T., & Schlund, S. (2021). Reasons and strategies for privacy features in tracking and tracing systems—a systematic literature review. Sensors, 21(13), 4501.

Rezayat, M. R., Yaghoubi, S., & Fander, A. (2020). A hierarchical revenue-sharing contract in electronic waste closed-loop supply chain. Waste Management, 115, 121-135.

Sharma, A. (2019). Game-theoretic analysis of pricing models in a dyadic supply chain with fairness concerns. International Journal of Strategic Decision Sciences (IJSDS), 10(2), 1-24.

Indexed at, Google Scholar, Cross Ref

Singh, M., Kumar, P., & Rathi, R. (2019). Modelling the barriers of Lean Six Sigma for Indian micro-small medium enterprises: An ISM and MICMAC approach. The TQM Journal, 31(5), 673-695.

Singh, A. (2016). Effectiveness Of Distribution Channels (Internet In Service Delivery With References To India. International Journal of Commerce and Management, 7, 34–36.

Google Scholar

Zhang, M., Fu, Y., Zhao, Z., Pratap, S., & Huang, G. Q. (2019). Game theoretic analysis of horizontal carrier coordination with revenue sharing in E-commerce logistics. International Journal of Production Research, 57(5), 1524-1551.

Indexed at, Google Scholar, Cross Ref

Received: 28-Apr-2024, Manuscript No. AMSJ-24-14765; Editor assigned: 29-Apr-2024, PreQC No. AMSJ-24-14765(PQ); Reviewed: 30-May-2024, QC No. AMSJ-24-14765; Revised: 13-Jun-2024, Manuscript No. AMSJ-24-14765(R); Published: 27-Jul-2024