Keywords

Fed Rate, Interest Rates, Global Indices.

Introduction

The primary cause of COVID-19 in India was registered in January 2020, and since then, the number of COVID cases in India has been steadily increasing. The Government of India has released travel restrictions similar to those issued during the previous pandemic, which spreads like same symptomatic as covid-19 viruses like SARS, Ebola, among others. The inflicting of self-isolation rules for all international travelers entering the country for a certain time of observation. The Indian government has banned travel visas for other countries until April 15th, after which other steps such as social distancing are proposed by the Indian Government to reduce the spread of this disease. On March 22nd, Prime Minister Sh. Narendra Modi proposed Janta Curfew to combat the spread of COVID-19; this activity resulted in the suspension of business operations and transportation services across the region. However, the Indian government's tries to reduce the extension of the COVID-19 pandemic affected the performance of the Select asset class rise (Equity, Debt, and Gold Markets). Because of the disturbances that occurred in the global economy, the Indian financial market also responded to the pandemic and experienced significant volatility. Due to the non-performance of financial transactions such as buying and selling asset class portfolios, market performance has hit rock bottom during this period. This has affected the steady decline of stock indices over the last four decades, and more than half of businesses have had an impact on their operations, with about 80 percent reporting a negative impact. We have also seen a decrease in cash flow, which has a direct negative impact on debt classes. The recent drop in gold is mostly due to the collapse of asset groups, which has resulted in margin calls.

Scope of the Study

The study aims to verify that there is a relationship and volatility effect of COVID 19 on select assets classes. The study considered the period 90 days from the official announcement of lockdown due to COVID 19 given by the Central Government of India. For this purpose, the following are the assets class considered for the research.

1. GOLD

2. DEBT

3. EQUITY

Objectives of the Study

1. To study the event analysis on the effect of COVID 19 on select assets class.

2. To examine the Covid19 affected the long-run or short-run relationship between select assets class.

3. To know the volatility effect of select assets class for the period of COVID 19.

Review of Literature

Curto & Serrasqueiro, (2021) in this paper the researcher hypothesize that not all stocks and sectors are affected equally by COVID-19 in terms of return volatility. Specifically, Jose & Pedro hypothesize that at least some sectors (Information Technology, Consumer Discretionary, Telecom Services, Consumer Staples and Energy) must show statistically significant differences. He analyze eleven SP500 sectors and FATANG stocks, estimating an Asymmetric Power GARCH model including a dummy variable to account for the outbreak. Results reveal an exacerbation of volatility after February 2020 and validate our hypothesis with few exceptions. Based on a likelihood ratio test, the null hypothesis is rejected in most cases in favor of our APARCH (1, 1).

In a study by Salisu et al. (2021) examined the hedging relationship between gold and US sectorial stocks during the COVID-19 pandemic. The researcher employs a multivariate volatility framework, which accounts for salient features of the series in the computation of optimal weights and optimal hedging ratios. He found evidence of hedging effectiveness between gold and sectorial stocks, albeit with lower performance, during the pandemic. Overall, including gold in a stock portfolio could provide a valuable asset class that can improve the risk-adjusted performance of stocks during the COVID-19 pandemic. In addition to that the estimated portfolio weights and hedge ratios are sensitive to structural breaks, and ignoring the breaks can lead to overestimation of the hedging effectiveness of gold for US sectorial stocks. Since the analysis involves sectorial stock data, they believed that any investor in the US stock market that seeks to maximize risk-adjusted returns is likely to find the results useful when making investment decisions during the pandemic.

Farid et al., (2021)investigated the evidence of dramatic changes in the structure and time-varying patterns of volatility connectedness across equities and major commodities (oil, gold, silver and natural gas) in the US economy before and during the COVID-19 outbreak. The study utilizes high frequency 5-min trading data of most actively traded US ETFs to construct the volatility connectedness network. He compute the intraday volatility estimates using MCS-GARCH model and then employ Diebold & Yilmaz, (2012) spillover index approach to approximate volatility spillovers between the financial markets. Their main findings showcase significant impact of COVID-19 pandemic on the volatility linkages of financial markets as the volatility connectedness among the different assets peaked during the outbreak.

Lahmiri & Bekiros, (2021) examined long memory (self-similarity) in digital currencies and international stock exchanges prior and during COVID-19 pandemic. Specifically, ARFIMA and FIGARCH models are respectively employed to evaluate long memory parameter in returns and volatility. The dataset contains 45 crypto currency markets and 16 international equity markets. The t-test and F-test are performed to estimated long memory parameters. The empirical findings of the research are first, the level of persistence in return series of both markets has increased during the COVID-19 pandemic. Second, during COVID-19 pandemic, variability level in persistence in return series has increased in both digital currencies and stock markets. Third, return series in both markets exhibited comparable level of persistence prior and during the COVID-19 pandemic. Fourth, return series in volatility series of crypto currency exhibited high degree of persistence compared to international stock markets during the COVID-19 pandemic. Therefore, it is concluded that COVID-19 pandemic significantly affected long memory in return and volatility of crypto currency and international stock markets. In addition to that the research suggest that the hybrid long memory model represented by the integration of ARFIMA-FIGARCH is significantly suitable to describe returns and volatility of crypto currencies and stocks and to reveal differences before and during COVID-19 pandemic periods.

Mazur et al. (2021) analysed the US stock market performance during the crash of March 2020 triggered by COVID-19. He found that natural gas, food, healthcare, and software stocks earn high positive returns, whereas equity values in petroleum, real estate, entertainment, and hospitality sectors fall dramatically. Moreover, loser stocks exhibit extreme asymmetric volatility that correlates negatively with stock returns. Firms react in a variety of different ways to the COVID-19 revenue shock. The analysis of the 8K and DEF14A filings of poorest performers reveals departures of senior executives, remuneration cuts, and (most surprisingly) newly approved cash bonuses and salary increases.

Kotishwar, (2020) investigated the impact of covid-19 virus spread on the stock markets. The study has considered the positive cases growth of six countries (USA, Spain, France, Italy, China and India), which were affected worst from 11th, March to April of 2020 (WHO declared the COVID 19 as pandemic on 11 March 2020). The study applied the VECM to know the relationship and observed that the Covid-19 having the significant negative long run relationship with all the selected countries stock indices. The CAAR model has been applied and observed that the all the selected countries indices are positively reacted more in post period compared with the pre period. The study states that the investors are considering the long-term strategy and investing at every low level.

Mahata et al. (2021) a stock price model has been developed to capture the price dynamics during shock and recovery phases of such crisis. The main variable and parameter of the model are the net fund flow due to institutional investors, and financial ant fragility of a company, respectively. The study assumed that during the crash, the stock price fall is independent. The study the effects of shock length and on the stock price during the crisis period using the obtained from both the synthetic fund flow data and real fund flow data. The study observed that the possibility of recovery of stock with, termed as quality stock, decreases with an increase in beyond a specific period. A quality stock with higher shows V-shape recovery and outperform others. The recovery period of quality stock is almost equal in the Indian market. Financially stressed stocks show L-shape recovery during the pandemic. The stock data and model analysis show that the investors, in the uncertainty like COVID-19, invest in the quality stocks to restructure their portfolio to reduce the risk. The study may help the investors to make the right investment decision during a crisis.

Hasan et al. (2021) empirically explored the effect of the COVID-19 pandemic on Islamic and conventional stock markets from a global perspective. The study explored the co-movement between Islamic and conventional stock markets. Two comparable pairs of conventional and Islamic stock indices – Dow Jones Index and FTSE Index are considered in this paper. Employing Wavelet-based multi-timescales techniques on the daily data from 21st January to 27th November 2020, the findings indicate that the pandemic creates identical volatility in both stock markets. The findings further suggest that both markets are strongly associated and tend to co-move highly during the sample period, rebutting the decoupling hypothesis of the Islamic stock market from the conventional market. However, the Shariah screening process fails to provide immunity to Islamic stock markets against financial crises. Investors should be aware that Islamic stocks' conservative features do not present a superior investment alternative, especially in economic turmoil.

Bing & Ma (2021) studied how institutional and foreign investors respond to the COVID-19 pandemic events in China. The results indicate that during the COVID-19 crisis foreign investors play a market stabilization role showing significant negative feedback trading, whereas institution investors do not stabilize the market. And compared to the pre-COVID-19 period, foreign investors even exhibit stronger negative feedback trading. Further analyses confirm that foreign investors’ negative feedback is mainly driven by their response to negative returns. Moreover, both institutional and foreign investors’ trading show stronger forecastability of future returns during the pandemic period. And the negative returns after foreigners’ selling and positive returns after institutional buying are much stronger during the crisis period.

Li et al. (2021) examined the impact of the COVID-19 pandemic on G20 stock markets from multiple perspectives. Measured the impact of COVID-19 on cross-market linkages and deeply explore the dynamic evolution of risk transmission relations and paths among G20 stock markets, statically and dynamically measure total, net, and pairwise volatility connectedness among G20 stock markets based on the DY approach by Diebold & Yilmaz, (2012, 2014). The results indicate that the total volatility connectedness among G20 stock markets increases significantly during the COVID-19 crisis, moreover, the volatility connectedness display dynamic evolution characteristics during different periods of the COVID-19 pandemic. Besides, they also found that the developed markets are the main spillover transmitters while the emerging markets are the main spillover receivers. Furthermore, to capture the impact of COVID-19 on the volatility spillovers of G20 stock markets, we individually apply the spatial econometrics methods to analyze both the direct and indirect effects of COVID-19 on the stock markets’ volatility spillovers based on the “volatility spillover network matrix” innovatively constructed in this paper. The empirical results suggest that stock markets react more strongly to the COVID-19 confirmed cases and cured cases than the death cases. In general, our study offers some reference for both the investors and policymakers to understand the impact of COVID-19 on global stock markets.

Espinosa-Méndez & Arias, (2021) investigated whether COVID-19 pandemic had an effect on herding behaviour in Europe. Using a sample from the stock exchanges of France (Paris), Germany (Frankfurt), Italy (Milan), United Kingdom (London) and Spain (Madrid), over the period from January 03, 2000 to June 19, 2020, the study found robust evidence that COVID-19 pandemic increased herding behaviour in the capital markets of Europe.

Baig & Chen (2021) Anecdotal evidence seems to suggest that the initial public offering (IPO) market performed remarkably well through the COVID-19 pandemic. To further understand this peculiar observation, the research carries out a comprehensive analysis of IPOs during the pandemic vis-a-vis IPOs before the pandemic. The findings imply that IPOs during the pandemic experience greater information uncertainty compared to those before the pandemic, and this greater uncertainty is mainly driven by the IPOs from the high-technology and the healthcare sectors. Furthermore, found that an average IPO firm experiences larger underpricing and more post-IPO return volatility as the pandemic and the associated government responses increase in severity before the offering. Overall, the study indicates that the COVID-19 pandemic had an adverse impact on the IPO market.

Hypothesis of the Study

H0: There is no long-run relationship exist between the COVID 19 and select asset class

H1: There is Long-run relationship exist between the COVID 19 and select asset class

H0: There is no volatility effect of select assets class for the period of COVID 19

H1: There is volatility effect of select assets class for the period of COVID 19.

Research Methodology

The data used for the research was collected from secondary sources. The information is obtained from various Records of Companies, Records Industry and Books, journals, e-journals, periodicals, and other published data and information. The period of the study to analyze the effect of covid 19 on select asset class growth in India was 90 days. The statistical tools adopted for this study were Cumulative Average Abnormal Return, Vector Error Correction Model, and Autoregressive Conditional Heteroskedasticity.

Data Analysis

Table 1 displays the Cumulative Average Abnormal Return value of Benchmark indices and the Sensex, which is -0.01, returns are -0.50, and risk is positive at 1.04. According to the values obtained from the table, it is discovered that during the study period, there are high abnormal returns, as well as a negative return, and the risk is low. As a result, it can be concluded that there is a strong abnormal return after COVID during the study period.

Table 1 Caar Model (Cumulative Average Abnormal Return) Nifty and Sensex
CAAR	Return	risk
-0.01	-0.50	1.04

Table 2 displays the Cumulative Average Abnormal Return value of Benchmark indices and the Debt, which is -0.3, returns and risk are -0.08 and -0.01 respectively. According to the values obtained from the table, it is discovered that during the study period, there are high abnormal returns, as well as a negative return, and the risk is high. As a result, it can be concluded that there is a strong abnormal return after COVID during the study period.

Table 2 Nifty and Debt
CAAR	Return	Risk
-0.43	-0.08	-0.01

Table 3 displays the Cumulative Average Abnormal Return value of Benchmark indices and the Gold, which is -0.38, returns and risk are -0.12474 and -0.00175 respectively. According to the values obtained from the table, it is discovered that during the study period, there are high abnormal returns, as well as a negative return, and the risk is high. As a result, it can be concluded that there is a strong abnormal return after COVID during the study period.

Table 3 Nifty and Gold
CAAR	RETURN	RISK
-0.38	-0.12474	-0.00175

Table 4 shows the Lag Order Selection for the Sensex with the Bench Mark variable. Five criterion tests select the lag order for the analysis. These tests are the LR test, Final Prediction Error test, Akaike Information Criterion test, Schwarz Information test, and Hanna-Quinn Information test. It is observed that all the tests have selected the lag order as 0 except the LR test. The selection of lag order is understood by the majority of the star mark against the lag order for all the criteria. But if more stars are occupied by lag 0, then by default lag 1 is the optimum model.

Table 4 VECM (Vector Error Correction Model)
1. Independent variable = Nifty   2. Dependent variable = Sensex Step 1: Lag Order Selection
VAR Lag Order Selection Criteria
Endogenous variables: DSENSEX NIFTY
Exogenous variables: C
Date: 05/21/21 Time: 09:50
Sample: 3/24/2020 6/21/2020
Included observations: 52
Lag	LogL	LR	FPE	AIC	SC	HQ
0	-608.8851	NA	54834913*	23.49558*	23.57063*	23.52435*
1	-607.0260	3.503738	59555905	23.57792	23.80307	23.66424
2	-604.3419	4.851972	62706403	23.62854	24.00378	23.77239
3	-604.2033	0.240001	72898844	23.77705	24.30238	23.97845
4	-602.3927	2.994394	79601529	23.86126	24.53669	24.12020
5	-595.0113	11.63995*	70309714	23.73120	24.55673	24.04769

Table 5 represents the Vector Error Model Analysis to know the relationship between Sensex and the independent variable Nifty. The result shows that the coefficient value of Nifty is 0.136601 at lag 1 which implies that there is a positive relationship between Sensex and Nifty.

Table 5 Step 2-VECM (Vector Error Correction Model)
	DSENSEX	DNIFTY
DSENSEX(-1)	0.402186	0.136601
	(1.72390)	(0.48699)
	[0.23330]	[0.28050]
DNIFTY(-1)	-1.758055	-0.586241
	(6.10814)	(1.72553)
	[-0.28782]	[-0.33975]
R-squared	-0.011031	-0.013438
Adj. R-squared	-0.029754	-0.032206
Sum sq. resids	31171939	2487660.
S.E. equation	759.7750	214.6340
F-statistic	-0.589173	-0.716049
Log-likelihood	-449.8915	-379.1026
Akaike AIC	16.13898	13.61081
Schwarz SC	16.21132	13.68314
Mean dependent	110.6420	34.40268
S.D. dependent	748.7181	211.2591
Determinant resid covariance (dof adj.)	1.62E+08
Determinant resid covariance		1.50E+08
Log-likelihood		-686.1277
Akaike information criterion		24.64742
Schwarz criterion		24.79209
Number of coefficients		4

Hypothesis

Null Hypothesis: There is no Long-run relationship exists between Nifty and Sensex.

Alternative Hypothesis: There is a Long-Run Relationship between Nifty and Sensex.

Table 6 represents the probability is greater than 0.05, So we need to accept the Null hypothesis and reject the Alternative hypothesis. Therefore, in VECM, there is no Long-run relationship exist between Nifty and Sensex.

Table 6 Step 3-Wald Test
Wald Test
System: %system
Test Statistic	Value	df		Probability
Chi-square	0.598393	2		0.7414
Null Hypothesis: C(1)=C(2)=0
Null Hypothesis Summary:
Normalized Restriction (= 0)			Value	Std. Err.
C(1)			0.402186	1.723895
C(2)			-1.758055	6.108145
Restrictions are linear in coefficients.

Table 7 shows the Lag Order Selection for the Debt with the Benchmark variable. Five criterion tests select the lag order for the analysis. These tests are LR test, Final Prediction Error test, Akaike Information Criterion test, Schwarz Information test, and Hanna-Quinn Information test. It is observed that all the tests have selected the lag order as 0 except LR test. The selection of lag order is understood by the majority of the star mark against the lag order for all the criteria. But if more stars are occupied by lag 0, then by default lag 1 is an optimum model (Farid et al., 2021).

Table 7 Step 1- Lag Order Model 2. Independent Variable = Nifty, Dependent Variable = Debt
VAR Lag Order Selection Criteria
Endogenous variables: DDEBT DNIFTY
Exogenous variables: C
Date: 05/21/21   Time: 11:18
Sample: 3/24/2020 6/21/2020
Included observations: 52
Lag	LogL	LR	FPE	AIC	SC	HQ
0	-467.6618	NA	239946.3*	18.06391*	18.13896*	18.09269*
1	-465.1164	4.797082	253815.7	18.11986	18.34500	18.20618
2	-464.0989	1.839352	284933.3	18.23457	18.60981	18.37843
3	-462.9973	1.906652	319203.1	18.34605	18.87138	18.54745
4	-457.0384	9.855018*	297150.5	18.27071	18.94614	18.52965
5	-453.6882	5.283057	306482.7	18.29570	19.12123	18.61219

Table 8 represents the Vector Error Model Analysis to know the relationship between Debt and the independent variable Nifty. The result shows that the coefficient value of Nifty is -9.169661 at lag 1 which implies that there is a negative relationship between Debt and Nifty.

Table 8 Step 2: VECM (Vector Error Correction Model)
Vector Error Correction Estimates
Date: 05/21/21   Time: 11:27
Sample (adjusted): 3/27/2020 5/20/2020
Included observations: 55 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
DDEBT(-1)	1.000000
DNIFTY(-1)	-0.061640
	(0.00931)
	[-6.61842]
C	1.355321
Error Correction:	D(DDEBT)	D(DNIFTY)
CointEq1	-0.131600	20.00730
	(0.05117)	(3.28444)
	[-2.57177]	[ 6.09155]
D(DDEBT(-1))	-0.412976	-9.169661
	(0.12047)	(7.73272)
	[-3.42792]	[-1.18583]
D(DNIFTY(-1))	-0.004219	0.067822
	(0.00210)	(0.13487)
	[-2.00788]	[ 0.50287]
C	-0.099742	-2.506070
	(0.45431)	(29.1598)
	[-0.21955]	[-0.08594]
R-squared	0.289873	0.590522
Adj. R-squared	0.248100	0.566435
Sum sq. resids	578.5251	2383400.
S.E. equation	3.368031	216.1789
F-statistic	6.939369	24.51627
Log-likelihood	-142.7532	-371.6510
Akaike AIC	5.336480	13.66004
Schwarz SC	5.482468	13.80602
Mean dependent	-0.086271	-3.106364
S.D. dependent	3.884151	328.3116
Determinant resid covariance (dof adj.)	525969.8
Determinant resid covariance	452247.1
Log-likelihood	-514.1878
Akaike information criterion	19.06137
Schwarz criterion		19.42634
Number of coefficients		10

D(DDEBT) = C(1)*( DDEBT(-1) - 0.0616401202299*DNIFTY(-1) + 1.35532082298 ) + C(2)*D(DDEBT(-1)) + C(3)*D(DNIFTY(-1)) + C(4)C(1)=C(3) = 0.

Hypothesis

Null Hypothesis: There is no Long-run relationship exists between Nifty and Sensex.

Alternative Hypothesis: There is a Long-Run Relationship between Nifty and Sensex.

Table 9 represents the probability is greater than 0.05, so we need to accept the Null hypothesis and reject the Alternative hypothesis. Therefore, in VECM, there is no Long-run relationship exist between Nifty and Debt.

Table 9 Step 3-Wald Test
Wald Test
System: %system
Test Statistic	Value	Df	Probability
Chi-square	7.403157	2	0.0247
Null Hypothesis: C(1)=C(3)=0
Null Hypothesis Summary:
Normalized Restriction (= 0)		Value	Std. Err.
C(1)		-0.136141	0.050147
C(3)		-0.004387	0.002064
Restrictions are linear in coefficients.

Table 10 shows the Lag Order Selection for the Gold with the Benchmark variable. Five criterion tests select the lag order for the analysis. These tests are LR test, Final Prediction Error test, Akaike Information Criterion test, Schwarz Information test, and Hanna-Quinn Information test. It is observed that all the tests have selected the lag order as 1 except the Schwarz information criterion. The selection of lag order is understood by the majority of the star mark against the lag order for all the criteria.

Table 10 Step 1- Lag Order Model 3. Independent Variable = Nifty    Dependent Variable = Gold
VAR Lag Order Selection Criteria
Endogenous variables: DGOLD DNIFTY
Exogenous variables: C
Date: 05/21/21   Time: 11:41
Sample: 3/24/2020 6/21/2020
Included observations: 52
Lag	LogL	LR	FPE	AIC	SC	HQ
0	-586.4388	NA	23127120	22.63226	22.70731*	22.66103
1	-580.8623	10.50960*	21771842*	22.57163*	22.79677	22.65794*
2	-579.7656	1.982484	24366726	22.68329	23.05853	22.82715
3	-578.4896	2.208455	27114925	22.78806	23.31340	22.98946
4	-574.9588	5.839285	27712528	22.80611	23.48154	23.06505
5	-574.1222	1.319404	31484074	22.92778	23.75330	23.24426

Table 11 represents the Vector Error Model Analysis to know the relationship between Gold and the independent variable Nifty. The result shows that the coefficient value of Nifty is -2.163360 at lag 1 which implies that there is a negative relationship between Gold and Nifty.

Table 11 STEP 2- VECM (Vector Error Correction Model)
Vector Error Correction Estimates
Date: 05/21/21   Time: 11:56
Sample (adjusted): 3/27/2020 5/20/2020
Included observations: 55 after adjustments
Standard errors in ( ) & t-statistics in [ ]
Cointegrating Eq:	CointEq1
DGOLD(-1)	1.000000
DNIFTY(-1)	-0.171359
	(0.02388)
	[-7.17616]
C	3.428308
Error Correction:	D(DGOLD)	D(DNIFTY)
CointEq1	-0.411181	7.092788
	(0.14766)	(1.07070)
	[-2.78473]	[ 6.62441]
D(DGOLD(-1))	-0.361772	-2.163360
	(0.13146)	(0.95327)
	[-2.75194]	[-2.26941]
D(DNIFTY(-1))	-0.029163	0.074027
	(0.01692)	(0.12272)
	[-1.72325]	[ 0.60323]
C	-0.410941	-0.853277
	(3.81164)	(27.6396)
	[-0.10781]	[-0.03087]
R-squared	0.438950	0.632507
Adj. R-squared	0.405947	0.610890
Sum sq. resids	40679.59	2139024.
S.E. equation	28.24250	204.7966
F-statistic	13.30031	29.25935
Log-likelihood	-259.7107	-368.6761
Akaike AIC	9.589480	13.55186
Schwarz SC	9.735468	13.69785
Mean dependent	-0.556364	-3.106364
S.D. dependent	36.64295	328.3116
Determinant resid covariance (dof adj.)		32485946
Determinant resid covariance		27932544
Log-likelihood		-627.5791
Akaike information criterion		23.18469
Schwarz criterion		23.54966
Number of coefficients		10

Hypothesis

Null Hypothesis: There is no Long-run relationship exists between Nifty and Sensex.

Alternative Hypothesis: There is a Long-Run Relationship between Nifty and Sensex.

The table 12 represents the probability is greater than 0.05, so we need to accept the Null hypothesis and reject the Alternative hypothesis. Therefore, in VECM, there is no Long-run relationship exist between Nifty and Debt.

Table 12 Step 3- Wald Test
Wald Test
System: %system
Test Statistic	Value	df	Probability
Chi-square	8.089458	2	0.0175
Null Hypothesis: C(1)=C(3)=0
Null Hypothesis Summary:
Normalized Restriction (= 0)		Value	Std. Err.
C(1)		-0.412195	0.145568
C(3)		-0.029281	0.016681
Restrictions are linear in coefficients.

Examine the COVID 19 Influence on the Volatility of Select Asset Class Growth (SENSEX)

H0: There is no volatility effect of select assets class for the period of COVID 19.

H1: There is a volatility effect of select assets class for the period of COVID 19.

Table 13 The ARCH LM test was used to determine heteroskedasticity, and the results show that the independent variable standard deviation is relative to the previous period. The significance of the prob. value is discovered. As a result, the analysis concludes that uncertainty exists in the Sensex, indicating the ARCH test.

Table 13 Arch Model (Autoregressive Conditional Heteroskedasticity)
Heteroskedasticity Test: ARCH
F-statistic	9.571661	Prob. F(1,54)	0.0029
Obs*R-squared	9.586623	Prob. Chi-Square(1)	0.0037

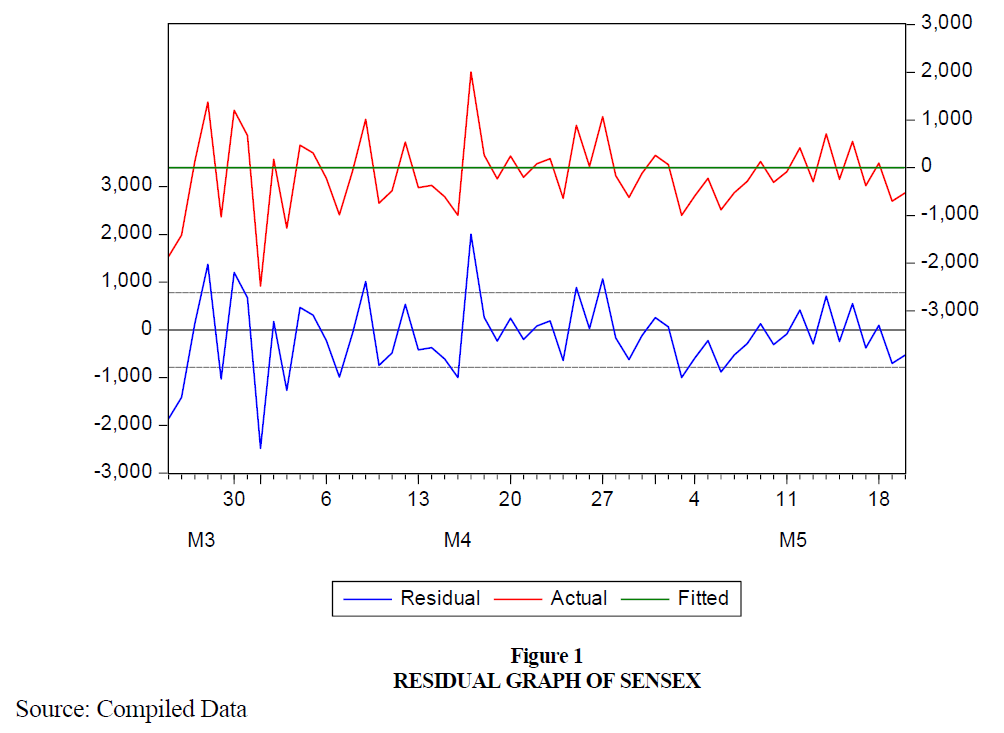
The Figure 1 indicates Sensex volatility. The X-axis is seen in the graph trend line is detected through the equipped lines, which indicates that the information is usually distributed. The instability of one cluster differs from that of the other. On the returns of Nifty and Sensex, the white noise test was used, resulting in the widespread sensation of stationary. The ARCH model can also be applied to understand the effect of volatility on selected growth in asset classes.

Table 14 of the ARCH family is designed to understand the effect on the volatility of the Sensex of Nifty volatility. The likelihood value of the Residual volatiles, i.e., 0.0175 is less than 0.05. It is observed. Hence, the Alternative hypothesis has been accepted and rejected by the Null hypothesis. The volatility of the Sensex can be inferred that the volatility of the Nifty is affected.

Table 14 Nifty Influence on Sensex
Dependent Variable: RSENSEX
Method: ML ARCH - Normal distribution (BFGS / Marquardt steps)
Date: 05/21/21   Time: 18:14
Sample (adjusted): 3/25/2020 5/20/2020
Included observations: 57 after adjustments
Convergence achieved after 9 iterations
Coefficient covariance computed using outer product of gradients
Presample variance: backcast (parameter = 0.7)
GARCH = C(2) + C(3)*RESID(-1)^2
Variable	Coefficient	Std. Error	z-Statistic	Prob.
C	-117.7052	80.77073	-1.457275	0.1450
	Variance Equation
C	435421.8	138606.9	3.141415	0.0017
RESID(-1)^2	0.304590	0.246983	1.233241	0.0175
R-squared	-0.000943	Mean dependent var		-141.3632
Adjusted R-squared	-0.000943	S.D. dependent var		777.4089
S.E. of regression	777.7752	Akaike info criterion		16.20826
Sum squared resid	33876320	Schwarz criterion		16.31579
Log-likelihood	-458.9354	Hannan-Quinn criter.		16.25005
Durbin-Watson stat	2.144701

Examine the COVID 19 influence on the volatility of Select Asset Class Growth (DEBT)

H0: There is no volatility effect of select assets class for the period of COVID 19.

H1: There is a volatility effect of select assets class for the period of COVID 19.

Table 15 The ARCH LM test was used to determine heteroskedasticity, and the results show that the independent variable standard deviation is relative to the previous period. The significance of the prob. value is discovered. As a result, the analysis concludes that uncertainty exists in the Debt, indicating the ARCH test.

Table 15 Arch LM Test of Debt
Heteroskedasticity Test: ARCH
F-statistic	9.08091	Prob. F(1,86)	0.0068
Obs*R-squared	9.082714	Prob. Chi-Square(1)	0.0037

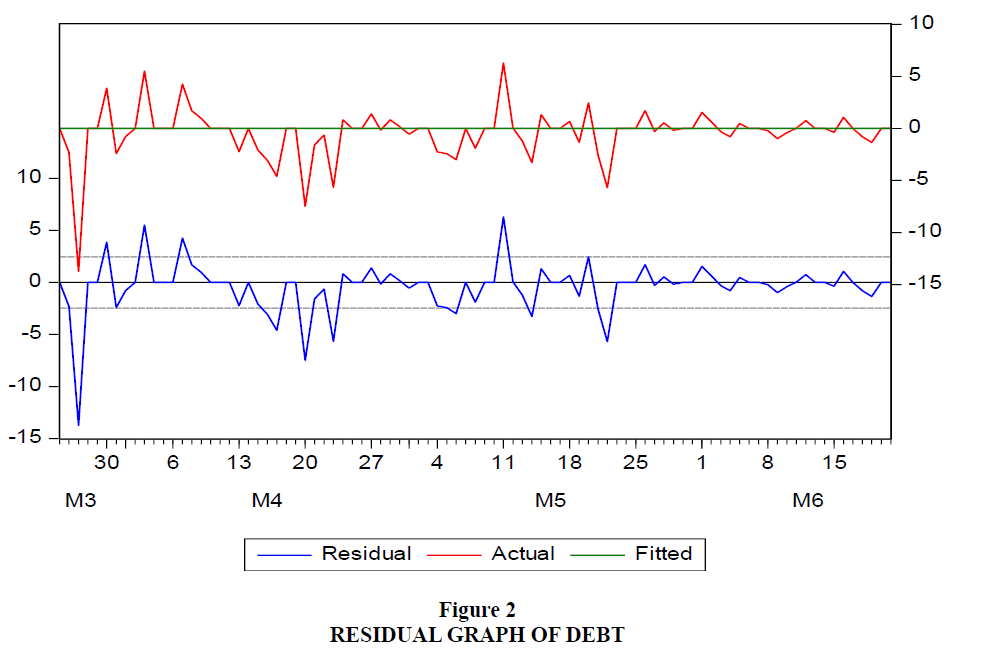
The Figure 2 indicates Debt volatility. The X-axis is seen in the graph trend line is detected through the equipped lines, which indicates that the information is usually distributed. The instability of one cluster differs from that of the other. On the returns of Nifty and Debt, the white noise test was used, resulting in the widespread sensation of stationary. An ARCH model can also be applied to understand the effect of volatility on selected growth in asset classes.

Table 16 of the ARCH family is designed to understand the effect on the volatility of the Debt of Nifty volatility. The likelihood value of the Residual volatiles, i.e., 0.0000 is less than 0.05. It is observed. Hence, the Alternative hypothesis has been accepted and rejected by the Null hypothesis. The volatility of the Debt can be inferred that the volatility of the Nifty is affected.

Table 16 Nifty Influence on Debt
Dependent Variable: RDEBT
Method: ML ARCH - Normal distribution (BFGS / Marquardt steps)
Date: 05/21/21   Time: 18:21
Sample (adjusted): 3/25/2020 6/21/2020
Included observations: 89 after adjustments
Failure to improve likelihood (non-zero gradients) after 29 iterations
Coefficient covariance computed using outer product of gradients
Presample variance: backcast (parameter = 0.7)
GARCH = C(1) + C(2)*RESID(-1)^2
Variable	Coefficient	Std. Error	z-Statistic	Prob.
	Variance Equation
C	5.557433	0.295660	18.79669	0.0000
RESID(-1)^2	-0.229479	0.001568	-18.79662	0.0000
R-squared	-0.033714	Mean dependent var		-0.443934
Adjusted R-squared	-0.022100	S.D. dependent var		2.431447
S.E. of regression	2.458167	Akaike info criterion		4.543473
Sum squared resid	537.7901	Schwarz criterion		4.599397
Log-likelihood	-200.1845	Hannan-Quinn criter.		4.566015
Durbin-Watson stat	1.691806

Examine the COVID 19 influence on the volatility of Select Asset Class Growth (GOLD)

H0: There is no volatility effect of select assets class for the period of COVID 19.

H1: There is a volatility effect of select assets class for the period of COVID 19.

Table 17 The ARCH LM test was used to determine heteroskedasticity, and the results show that the independent variable standard deviation is relative to the previous time. The significance of the prob. value is discovered. As a result, the analysis concludes that uncertainty exists in the Gold, indicating the ARCH test.

Table 17 Arch Lm Test of Gold
Heteroskedasticity Test: ARCH
F-statistic	9.330828	Prob. F(1,61)	0.0073
Obs*R-squared	9.339832	Prob. Chi-Square(1)	0.0599

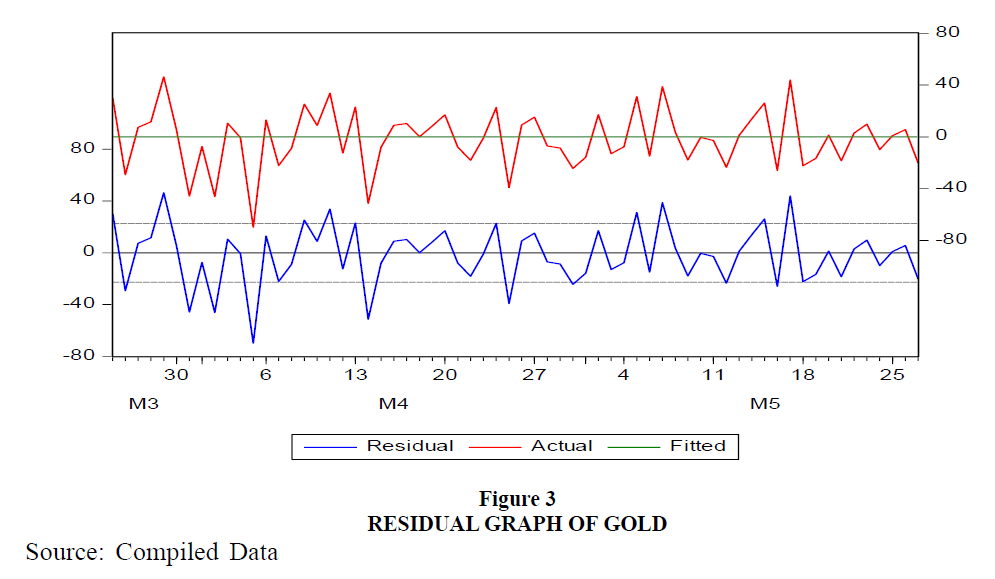
The figure 3 indicates Gold volatility. The X-axis is seen in the graph trend line is detected through the equipped lines, which indicates that the information is usually distributed. The instability of one cluster differs from that of the other. On the returns of Nifty and Gold, the white noise test was used, resulting in the widespread sensation of stationary. The ARCH model can also be applied to understand the effect of volatility on selected growth in asset classes.

Table 18 of the ARCH family is designed to understand the effect on the volatility of the Gold of Nifty volatility. The likelihood value of the Residual volatiles, i.e., 0.2582 is greater than 0.05. It is observed. Hence, the Null hypothesis has been accepted and rejects the Alternative hypothesis. The volatility of the Gold can be inferred that the volatility of the Nifty is not affected.

Table 18 Influence on Gold
Dependent Variable: RGOLD
Method: ML ARCH - Normal distribution (BFGS / Marquardt steps)
Date: 05/22/21   Time: 17:27
Sample (adjusted): 3/25/2020 5/27/2020
Included observations: 64 after adjustments
Convergence achieved after 17 iterations
Coefficient covariance computed using outer product of gradients
Presample variance: backcast (parameter = 0.7)
GARCH = C(1) + C(2)*RESID(-1)^2
Variable	Coefficient	Std. Error	z-Statistic	Prob.
	Variance Equation
C	555.9329	94.42856	5.887338	0.0000
RESID(-1)^2	-0.091506	0.080934	-1.130625	0.2582
R-squared	-0.006108	Mean dependent var		-1.770312
Adjusted R-squared	0.009612	S.D. dependent var		22.83032
S.E. of regression	22.72033	Akaike info criterion		9.112297
Sum squared resid	33037.67	Schwarz criterion		9.179762
Log-likelihood	-289.5935	Hannan-Quinn criter.		9.138875
Durbin-Watson stat	2.365495

Findings of the Study

1. In the study's CAAR model, select assets in the COVID 19 lockdown have a high abnormal return. It was also discovered that debt has high abnormal returns when compared to the remaining asset classes.

2. It indicates that equity is positively related to the benchmark for the period of COVID 19, whereas debt and gold are negatively related to the benchmark indices.

3. It estimates that there is a significant volatility effect for the selected asset classes, and signifies that equity and gold are experienced high volatility after the announcement of a lockdown.

4. It synchronized that debt had a significantly negative volatility effect during the study period.

5. The study observed abnormal movement of the stock market due to the covid-19 effect. Therefore, the study suggests taking the position of the investment by understanding the fundamentals of the markets in the long term.

6. The study found that the downturn of the economy boosts the gold prices upside by pushing the equity downward. Therefore, the study suggests the investors focus on gold investments if the economy is in a bearish trend for the long term due to the pandemic effect.

7. The study suggests the investors be flexible at all times. As per the market conditions, portfolios need to shuffle to maximize the returns of the investments in different performing asset classes.

Conclusion of the Study

The study attempted to determine the relationship and volatility effect of COVID 19 on a selected asset class. The study considered 90 days from the official announcement of lockdown due to COVID 19 given to the Central Government of India for this purpose. There were three asset classes considered: equity, debt, and gold. It concluded that, for the COVID 19 period, there is a high abnormal return in select assets and that debt has a high abnormal return when compared to the remaining asset classes. Furthermore, the study indicates that a significant relationship exists between the asset classes and the benchmark indices during the study period. It also states that, during the study period or after the announcement of the lockdown, equity and gold experienced high volatility, whereas debt experienced negative volatility.

References

Baig, A. S., & Chen, M. (2021). Did the COVID-19 pandemic (really) positively impact the IPO Market? An Analysis of information uncertainty. Finance Research Letters, 102372.

Bing, T., & Ma, H. (2021). COVID-19 pandemic effect on trading and returns: Evidence from the Chinese stock market. Economic Analysis and Policy, 71, 384–396.

Curto, J. D., & Serrasqueiro, P. (2021). The impact of COVID-19 on S&P500 sector indices and FATANG stocks volatility: An expanded APARCH model. Finance Research Letters, 102247.

Espinosa-Méndez, C., & Arias, J. (2021). COVID-19 effect on herding behaviour in European capital markets. Finance Research Letters, 38, 101787.

Farid, S., Kayani, G. M., Naeem, M. A., & Shahzad, S. J. H. (2021). Intraday volatility transmission among precious metals, energy and stocks during the COVID-19 pandemic. Resources Policy, 72, 102101.

Hasan, M. B., Mahi, M., Hassan, M. K., & Bhuiyan, A. B. (2021). Impact of COVID-19 pandemic on stock markets: Conventional vs. Islamic indices using wavelet-based multi-timescales analysis. The North American Journal of Economics and Finance, 58, 101504.

Kotishwar, A (2020). Impact of Covid-19 Pandemic on Stock Market with Reference to Select Countries-A Study. Academy of Accounting and Financial Studies Journal, 24(4), 72–80.

Lahmiri, S., & Bekiros, S. (2021). The effect of COVID-19 on long memory in returns and volatility of cryptocurrency and stock markets. Chaos, Solitons & Fractals, 151, 111221.

Li, Y., Zhuang, X., Wang, J., & Dong, Z. (2021). Analysis of the impact of COVID-19 pandemic on G20 stock markets. The North American Journal of Economics and Finance, 58, 101530.

Mahata, A., Rai, A., Nurujjaman, M., & Prakash, O. (2021). Modeling and analysis of the effect of COVID-19 on the stock price: V and L-shape recovery. Physica A: Statistical Mechanics and Its Applications, 574, 126008.

Mazur, M., Dang, M., & Vega, M. (2021). COVID-19 and the march 2020 stock market crash. Evidence from S&P1500. Finance Research Letters, 38, 101690.

Salisu, A. A., Vo, X. V., & Lucey, B. (2021). Gold and US sectoral stocks during COVID-19 pandemic. Research in International Business and Finance, 57, 101424.