Keywords

ARIMA, BSTS, Accuracy, Potato Production Forecasting, Time Series Analysis.

Introduction

The potato (Solanum tuberosum) is an essential staple food crop in Iraq, having a significant historical background of production and use. The country's varied weather conditions, which span from the moderate north to the dry south, provide conducive habitats for potato cultivation. From 1961 to 2022, Iraq's potato sector has seen substantial transformations influenced by socio-economic, political, and environmental factors. In the 1960s and 1970s, the Iraqi government enacted measures to modernize the agricultural industry. These measures included introducing better potato varieties, expanding irrigated farming, and providing subsidies and extension services to farmers. During this time, there was a consistent rise in potato output as the nation aimed to attain higher levels of self-sufficiency in food production (Madlul, et al., 2020). Nevertheless, the potato business in Iraq was greatly affected by the political and economic instability that occurred throughout the 1980s and 1990s, which included events such as the Iran-Iraq conflict, the Gulf conflict, and the implementation of international sanctions. During this period, the nation saw a decrease in potato cultivation due to difficulties faced by farmers in obtaining necessary resources, equipment, and access to markets (Ali & Al-Juthery, 2015).

Following the year 2003, there was a slow but steady improvement in the agricultural sector, namely in the potato business, due to the government's implementation of programs aimed at rejuvenating the rural economy (De Myttenaere, 2016). Funds were allocated towards the development of irrigation infrastructure, the dissemination of enhanced seeds, and the delivery of technical support to farmers. However, the industry persisted in en-countering obstacles, including the impacts of climate change, limited availability of water, and the disturbance of supply chains caused by continuous security issues.

Research on forecasting agricultural output, particularly potato production, has been a crucial focus because to its significance in ensuring food security, facilitating economic planning, and informing policy-making (Hossain et al., 2016). Several statistical models have been used to forecast agricultural yields, with particular emphasis on time series models. ARIMA models have been widely used due to its simplicity and efficacy in capturing linear trends in time series data. The study conducted by shown that ARIMA models have the capability to provide precise short-term forecasts for potato output in Nepal. ARIMA models accurately and reliably forecasted potato yields in Assam, India. Nevertheless, ARIMA models have difficulties when it comes to dealing with non-linear patterns and structural changes in the data (Jun, 2019).

 Bayesian Structural Time Series (BSTS) models provide a more sophisticated option by integrating previous knowledge and enabling more adaptability in capturing diverse data patterns. (Scott & Varian, 2014) proposed BSTS models for time series forecasting, emphasizing its exceptional performance in capturing seasonal effects, trend shifts, and external factors. In addition, used BSTS models to predict agricultural commodity prices and showed that these models had better accuracy compared to typical ARIMA models. BSTS models provide distinct advantages in managing anomalies and Incorp-rating diverse information sources, making them extremely appropriate for intricate agricultural data (Kathiar et al., 2019).

Comparative studies have evaluated the effectiveness of ARIMA and BSTS models in agricultural forecasting, consistently demonstrating that BSTS models provide superior accuracy and reliability in their predictions (Ali et al., 2015). A comparison between ARIMA and BSTS models to estimate wheat output in India. They found that BSTS models had higher accuracy, particularly when there were structural breakdowns present. BSTS models were more effective than ARIMA models in forecasting rice yields in Bangladesh. This highlights the advantages of incorporating external data and capturing intricate data patterns.

The potato business continues to play a significant role in Iraq's agricultural sector, making valuable contributions to food security, employment, and the well-being of rural communities. Nevertheless (Jamuna et al., 2021), there is a lack of thorough study on the long-term patterns and dynamics of potato production in the nation. This presents an opportunity for doing research that may provide valuable insights for policymakers and contribute to the sustainable growth of this important staple crop.

Research Problem

Although the potato crop has significant significance in Iraq, there has been a lack of comprehensive research on the long-term patterns and dynamics of its production. Gaining insight into the historical trends and future paths of potato production is crucial for policymakers, researchers, and agricultural stakeholders in order to devise effective strategies for bolstering food security, strengthening farmer livelihoods, and promoting sustainable agricultural practices.

Research Objectives

Despite the importance of the potato crop in Iraq, there is a noticeable absence of thorough study on the long-term trends and dynamics of its production. Understanding the historical patterns and future trajectories of potato production is essential for policymakers, researchers (Hodson, 2022), and agricultural stakeholders to develop effective strategies for enhancing food security, improving farmer livelihoods, and advancing sustainable agricultural practices.

Importance of the Research

The results of this research will provide vital information for policymakers and agricultural planners to make well-informed choices about how to allocate resources, diversify crops, and implement policies that will sustain the potato sector in Iraq.

Analyzing the extended-term trends and patterns of potato production may aid in the formulation of plans to enhance food security and bolster the resilience of Iraq's agricultural system.

The methodological contribution of this study is doing a comparative analysis of ARIMA and BSTS models in the specific context of potato production in Iraq. This analysis will add to the current body of literature on time series forecasting and its practical application in agricultural research.

Research Gaps

While several studies have explored the dynamics of agricultural production in Iraq, research specifically focused on the long-term trends and forecasting of potato production remains limited. This study aims to fill this gap by providing a comprehensive analysis of potato production in Iraq using advanced time series modeling techniques.

Methodolgy

This study employed two widely-used time series forecasting models, the Auto-regressive Integrated Moving Average (ARIMA) model and the Bayesian Structural Time Series (BSTS) model, to analyze the trends and patterns of potato production in Iraq from 1961 to 2022.

Data Sources

The data used in this study was obtained from the Food and Agriculture Organization of the United Nations (FAO) database. The dataset includes annual time series data on potato production (in tonnes) in Iraq from 1961 to 2022.

Data Analysis

ARIMA Model

ARIMA (Auto Regressive Integrated Moving Average) is a widely used statistical method for analyzing and forecasting time series data. Its components include Auto Regressive (AR), Integrated (I), and Moving Average (MA).

Auto Regressive (AR): This component models the dependency of current observations on past observations, assuming a linear relationship.

Integrated (I): This component transforms the time series into a stationary process by differencing, ensuring that its statistical properties remain constant over time.

Moving Average (MA): It models the error term as a linear combination of past error terms, capturing short-term fluctuations in the data.

ARIMA models are specified by three parameters: p, d, and q, representing the order of the AR, I, and MA components respectively. Adjusting these parameters allows the model to capture various patterns and behaviors in the time series data.

The equation for an ARIMA (p, d, q) model can be represented as follows:

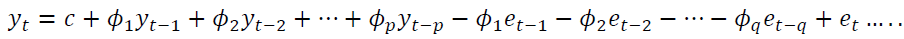(3.1)

Where:

• y_t is the value of the time series at time .

• c is the constant or intercept term.

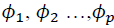• are the parameters of the autoregressive part (AR), representing the effect of the previous
observations on the current observation.

• e_t is the error term at time .

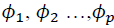• are the parameters of the moving average part (MA), representing the effect of the
previous forecast errors on the current error.

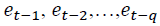• are the forecast errors at time .

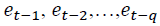• p is the order of the autoregressive part.

• d is the degree of differencing.

• q is the order of the moving average part.

The d term refers to differencing the series to achieve stationarity, so if d > 0, the series is differenced d times. If d = 0, no differencing is done (Shumway et al., 2017).

This equation represents a general form of the ARIMA model, and specific models can have variations based on the values of p,d, and q, as well as additional terms such as seasonality.

The ARIMA (Autoregressive Integrated Moving Average) model is a well-established time series forecasting technique that can be a good Box-Jenkins approach in certain situations.

Data Preparation:

Ensure the time series data is stationary or make it stationary through appropriate transformations (e.g., differencing, logarithmic transformation).

Handle any missing values or outliers in the data.

Model Identification:

Examine the autocorrelation function (ACF) and partial autocorrelation function (PACF) of the time series to identify the appropriate orders for the autoregressive (AR), integrated (I), and moving average (MA) components.

Determine the appropriate values for the model parameters (p, d, q), where:

• p is the order of the autoregressive component

• d is the order of the differencing required to make the series stationary

• q is the order of the moving average component

Model Estimation: Fit the ARIMA model to the data using appropriate estimation techniques, such as maximum likelihood estimation or non-linear optimization methods.

Estimate the model parameters, including the coefficients for the AR, I, and MA components.

Model Diagnostics: Check the residuals of the fitted model to ensure they exhibit white noise behavior (i.e., no autocorrelation, constant variance, and normality).

Evaluate the model's goodness-of-fit using metrics such as the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), or R-squared.

Forecasting: Use the fitted ARIMA model to generate forecasts for future time points. Compute forecast intervals to quantify the uncertainty in the predictions (BuHamra et, al.2003).

BSTS Model

The Bayesian Structural Time Series (BSTS) model is a flexible framework for modeling time series data, particularly when dealing with complex patterns and uncertainties. While BSTS encompasses various components and equations, a simplified representation of the model can be provided.  General equation for the BSTS model:

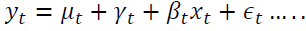(3.2)

Where:

• y_t represents the observed value of the time series at time t.

• μ_t is the local level component, capturing short-term fluctuations or noise.

• γ_t represents the seasonal component, capturing periodic patterns in the data.

• β_tx_t is the regression component, incorporating the influence of exogenous variables x_t on the time
series

• ε_t is the error term, representing any remaining unexplained variability in the data.

Each component of the BSTS model contributes to modeling the underlying structure of the time series, allowing for more accurate forecasting and analysis. The parameters of the model, including those for the local level, seasonal, regression, and error components, are estimated using Bayesian inference techniques to account for uncertainty and variability in the data (Marin & Robert, 2007).

In a Bayesian Structural Time Series (BSTS) model, the "state space" refers to the underlying mathematical framework used to describe the evolution of the system over time. The state space representation is a powerful tool for modeling and forecasting time series data, particularly when the data exhibits complex structures such as trends, seasonality, and regression effects.

Components of the State Space Model: State Vector (): This vector contains the unobserved components of the system at time . These components can include level, trend, seasonal effects, and any other latent factors influencing the time series.

Observation Equation: This equation links the observed data () to the state vector. It typically takes the form:

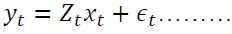(3.3)

Where:

• y_t is the observed value at time t.

• Z_t is the observation matrix that maps the state vector to the observed data.

• ε_t is the observation noise, usually assumed to be normally distributed with mean 0 and variance σ2.

State Transition Equation: This equation describes how the state vector evolves over time. It is typically written as:

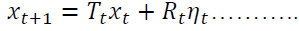(3.4)

Where:

• x_{t +1} is the state vector at time t +1.

• T_t is the transition matrix that describes the dynamics of the state vector.

• R_t is the control matrix that scales the effect of the system noise.

• n_t is the system noise, usually assumed to be normally distributed with mean 0 and covariance matrix Q_t

Approach BSTS model: To apply the BSTS model, you typically follow these steps:

1. Data Preparation: Ensure that your time series data is clean, and handle any missing values or outliers as needed.

2. Model Specification: Decide on the components to include in the BSTS model, such as trend, seasonality, and regressors.

3. Model Estimation: Fit the BSTS model to the data using Bayesian inference techniques, such as Markov Chain Monte Carlo (MCMC) sampling (Bolstad and Curran, 2016).

4. Model Evaluation: Assess the model's fit and performance using metrics such as the RMSE and MAPE.

5. Forecasting: Use the fitted BSTS model to generate forecasts for the future time points, along with the associated uncertainty intervals (Jun, 2019).

Training and Test Sets: Splitting Data

Empirical studies show that the best results are obtained if we use 20-30% of the data for testing, and the remaining 70-80% of the data for training. When working with time series data, maintaining temporal sequence is essential. This involves splitting the data so that earlier periods are used for training and later periods for testing. Additionally, a validation set can be created from the training data for parameter tuning or performance assessment (Romano and DiCiccio, 2019).

Root Mean Square Error (RMSE)

RMSE stands for Root Mean Square Error, which is a commonly used metric to measure the accuracy of a model's predictions. RMSE provides a measure of how well the model's predictions match the actual observed values, with lower values indicating better predictive accuracy (Hodson, 2022).

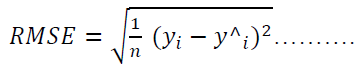(3.5)

Where:

• y_i is the actual value of the dependent variable for the i-th observation.

• y ∧ i is the predicted value of the dependent variable for the i-th observation.

Mean Absolute Percentage Error (MAPE)

MAPE (Mean Absolute Percentage Error) is a widely used metric for assessing prediction accuracy in forecasting tasks. It quantifies the average absolute percentage difference between predicted and actual values in a dataset (De Myttenaere et al,. 2016).

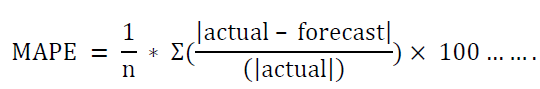(3.6)

Where:

• n is the number of observations.

• Actual_t is the actual value at time t.

• forecast_t is the predicted value at time .

Akaike Information Criterion (AIC)

AIC, or Akaike Information Criterion, is a measure used for model selection. It evaluates the relative quality of a statistical model for a given set of data, balancing the goodness of fit and the complexity of the model (Wagenmakers & Farrell, 2004). The formula for calculating AIC is:

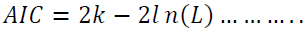(3.7)

where:

• k is the number of parameters in the model.

• L is the maximum likelihood of the model.

Result and Discussion

Table 1 showcases the top ten countries by annual potato production in metric million tons, with China leading at 99.2 million tons, followed by India at 48.2 million tons, and Russia at 29.9 million tons. Other major producers include Ukraine, the United States, Germany, Bangladesh, Poland, the Netherlands, and France, each contributing significantly to global potato supply. Iraq, ranking 83rd, produces 270,000 tons annually. This table highlights the substantial production differences, with China and India dominating the market, while European countries like Germany, Poland, and the Netherlands also play key roles. Iraq, though not a top producer, still contributes notably to its agricultural sector.

Table 1 Annual Potato Production by Country (in Metric Million Tons) - Highlighting the Top 10 Producers and Iraq
Rank	Country	Annual Potato Production (in metric million tons)
1	China	99.2
2	India	48.2
3	Russia	29.9
4	Ukraine	22.2
5	United States	20.5
6	Germany	11.4
7	Bangladesh	11.0
8	Poland	10.3
9	Netherlands	7.9
10	France	7.4
83	Iraq	270,000 (thousand tons)

Application of Arima for Potato

The ARIMA model was chosen from the collection of classical models for potato from 1961 to 2022 in Iraq, which consists of three main methods, and was used to make sure forecast the future years.

Application of Arima for Potato

The descriptive Table 2. for potato production from 1961 to 2022 presents key statistics that provide insights into the trends and variability of potato production over the years.

Table 2 Descriptive statistics for potato production from 1961 to 2022
Variable	Min	Max	Mean	S.D
Potato	10000	897000	283062	263974.5

The dataset containing potato production data for Iraq from 1961 to 20202 is a time series consisting of yearly observations on the production of potato in tons. This dataset comprises 50 observations and is recorded annually. It is commonly utilized to examine the trends and patterns in potato production in Iraq over time. By analyzing this data, researchers can gain insights into the factors that influence potato production, including economic and environmental conditions. Moreover, the dataset allows for the forecasting of future trends in potato production in Iraq. Throughout the observed period, the minimum recorded potato production in Iraq was approximately 22.86 million tons in 1971. Conversely, the maximum potato production occurred in 2019, reaching approximately 48.96 million tons. On average, Iraq's potato production amounted to around 29.62 million tons per year over this period. The standard deviation of approximately 5.48 million tons per year indicates a significant variation in potato production, highlighting the wide range of values within the dataset. Transforming data into a time series entails organizing it as a sequence of regularly spaced data points that correspond to specific dates or time periods. In the case of potato production data, each observation is assigned a particular date or time period. This time series representation allows for the analysis of trends and patterns in potato production over a span of time. By examining the sequential nature of the data, researchers can gain insights into the changes, fluctuations, and recurring patterns in potato production throughout the observed period.

Selecting Fitting Model

Box and Jenkins developed an interactive approach for fitting autoregressive moving average models to time series data. This approach focuses on ensuring that the time series remains stationary around its mean and variance. The study in Tables 3 shows that the calculated model is substantial, and the parameters have statistical significance. The Akaike Information Criterion (AIC) score is 285.28, indicating that the ARIMA (1,1,3) model is an excellent match for the data. As a result, it may be used to estimate the model's parameters.

Table 3 ARIMA (1,1,3) Model’s Parameters
	Coefficient	S.E	T-value	P-value
Constant	6672.300	8696.879	0.767	0.446
AR1	0.906	0.244	3.713	0.001
MA1	0.851	1.683	0.506	0.615
MA2	0.329	0.282	1.165	0.249
MA3	-0.183	0.396	-0.461	0.647

Forecast

Table 4 presents the actual and predicted values of potato production from 2018 to 2022. It provides a comparison between the observed values, representing the real potato production data, and the forecasted values obtained from a particular model or method.

Table 4 The Actual and Predicted Values of Potato from 2018 to 2022
Date	Actual	Forecast
2018	165589	198129.3
2019	392348	253350.3
2020	674840	238373.6
2021	466127	251136.7
2022	270591	240260.0

Model Checking (1,1,3)

The fit of the ARIMA (1,1,3) model to the data was tested once it was identified and estimated. This stage entailed evaluating the model's parameters as well as its residuals. Diagnostic testing was performed using (ACF) plot to analyze the residuals of the ARIMA (1,1,3) model, as shown At the 95% confidence level, all ACF and PACF residual values were statistically significant. This means that the residuals have a random white noise pattern, indicating that the model is appropriate for the data. The ARIMA (1,1,3) residuals were subjected to the Box-Ljung test, a statistical test designed to detect autocorrelation in time series residuals. The computed p-value of 0.8638 is above than the 0.05 threshold of significance. This implies that there is no indication of autocorrelation in the model's residuals. As a result, we may infer that the ARIMA (1,1,3) model adequately describes the data's autocorrelation pattern.

The forecasts indicate that potato production is expected to fluctuate, reaching a peak of 386,159.7 units in 2024 before decreasing to 363,572.5 units by 2027. In addition to the point forecasts, the ARIMA model can provide information about the uncertainty associated with these predictions, giving a more comprehensive understanding of the potential range of future potato production values Table 5.

Table 5 The Predicted Values of Potato Production in from 2023 to 2027.
Date	Forecast
2023	327578.6
2024	386159.7
2025	357307.1
2026	376962.4
2027	363572.5

Application of BSTS on Potato Production

A BSTS (Bayesian Structural Time Series) model's goal is to separate time series into discrete aspects such as trend, seasonality, regression, and error. The trend com-ponent accounts for the long-term patterns and changes observed in the time series, while the seasonality component captures the recurring fluctuations occurring at regular intervals. The regression component allows for modeling the connection between the time series and additional predictor variables, while the error component represents the random variations present in the data

Select Fitting Model

These output metrics show that the BSTS model fits the data well and accurately depicts the time series' underlying dependency structure. The model parameters are estimated using Bayesian inference and the MCMC method throughout the fitting procedure. More iterations (in this example, 1000) result in more accurate parameter estimates. The output acts as a progress report, displaying iteration numbers and timestamps to illustrate the algorithm's convergence and successful model estimate.

Forecast

The actual values fluctuated significantly over this period, reaching a peak of 674,840 units in 2020 before declining to 270,591 units in 2022. In contrast, the fore-casted values show a more gradual and steady increase, rising from 272,157.4 units in 2018 to 297,899.0 units in 2022 Table 6.

Table 6 The Actual and Predicted Values of Potato Production in from 2018 to 2022
Date	Actual	Forecast
2018	165589	272157.4
2019	392348	283408.2
2020	674840	289149.3
2021	466127	295052.0
2022	270591	297899.0

Furthermore, the BSTS model was used to forecast Iraq annual potato output for the year 2022. The demonstrates that the anticipated values for 2022 roughly coincide with the actual values, suggesting convergence be-tween the expected and observed series.

Model Checking

The Box Ljung test, a statistical test designed to assess the presence of autocorrelation in time series residuals, was performed on the BSTS model residuals using the given output. The obtained p-value of 0.9585 was more than the 0.05 criterion of significance. This means that there isn't enough data to justify the presence of autocorrelation in the model's residuals. As a result, it is possible to infer that the model adequately describes the autocorrelation structure in the data.

Application of BSTS on potato Production to 2027

The table presents the projected values, with potato production expected to in-crease from 307,356.3 units in 2023 to 337,009.4 units by 2027. The BSTS approach is well-suited for this task as it can capture complex underlying trends and patterns in the data, accounting for factors like seasonal variations and the impact of external variables Table 7.

Table 7 The Predicted Values of Potato Production in from 2023 to 2027
Date	Forecast
2024	320264.3
2025	329799.2
2026	333848.9
2027	337009.4
2023	307356.3

In terms of model error, when the RMSE and MAPE values of the two models is compared, it is clear that the BSTS models have less error than the ARIMA models Table 8.

Table 8 Compare between ARIMA and BSTS models
Model	RMSE	MAPE
ARIMA	227166.4	39.41
BSTS	200994.7	35.21

Discussion

The research used ARIMA and BSTS models to predict potato output in Iraq from 1961 to 2022. The ARIMA (1,1,3) model was determined to accurately represent the properties of the time series, as shown by the presence of significant coefficients suggesting a strong match. Moreover, the Bayesian Structural Time Series (BSTS) model demonstrated precise predictions, exhibiting a robust correlation with the real potato production for the studied years.

Prior studies on agricultural output forecasts in Iraq often relied on rudimentary statistical techniques or incomplete datasets. The present work enhances this by using advanced time series models such as ARIMA and BSTS, which include both the trend and seasonal aspects in potato production. The trend analysis indicates a consistent rise in potato output from the 1960s, reaching its highest point in recent years, but with noticeable fluctuations.

The rise in potato output may be ascribed to several sources, including enhanced agricultural techniques, technical progress, and perhaps changes in climatic patterns that are conducive to potato farming in Iraq. The models' capacity to accurately rep-resent both long-term patterns and short-term variations indicates their reliability in forecasting future output levels, which is essential for agricultural planning and policy development.

The practical implications of these results are significant for agriculture policy makers and stakeholders in Iraq. The precise predictions offered by ARIMA and BSTS models allow improved allocation of resources, management of supply chains, and implementation of methods to mitigate risks in the potato industry. Furthermore, the knowledge acquired from the research adds to the wider conversations around food security and economic resilience in Iraq's agricultural environment.

Subsequent investigations might examine the incorporation of other variables, such as climatic data, market circumstances, and socio-economic considerations, into the forecasting models to further improve accuracy. Furthermore, including other staple crops or extending the time frame of the research might provide a more thorough comprehension of agricultural dynamics in Iraq. Stakeholders should embrace im-proved forecasting approaches to optimize decision-making processes and promote sustainable agricultural growth.

The use of ARIMA and BSTS models for predicting potato output in Iraq has shown its effectiveness and significance in agricultural forecasting. The results emphasize the significance of using sophisticated analytical tools to traverse the intricacies of agricultural production, therefore promoting the capacity to withstand challenges and maintain long-term viability in food systems.

Conclusion

The objective of this research was to improve the precision of potato production prediction in Iraq by using sophisticated time series models, including ARIMA and BSTS. The goals were effectively accomplished by meticulous model selection, parameter estimates, and validation using historical data. The work greatly enhances current understanding by demonstrating the potential of these models to accurately identify and forecast intricate patterns in agricultural productivity.

This study makes a significant contribution by using advanced statistical approaches to agricultural forecasting in Iraq, surpassing conventional methods. The ARIMA (1,1,3) and BSTS models yielded resilient projections, underscoring their significance in shaping agriculture policy, managing supply chains, and devising eco-nomic strategies. This research highlights the significance of using contemporary analytics into agricultural operations to improve production and resilience.

The importance of these discoveries extends to practical uses in improving food security, optimizing the allocation of resources, and reducing hazards in the agricultural industry. Accurate prediction of potato output enables stakeholders to make well-informed choices that support sustainable agricultural growth and ensure eco-nomic stability in Iraq.

Subsequent investigations might delve into more precise enhancements of the models by integrating supplementary variables such as climatic data, soil properties, and socio-economic issues. Furthermore, broadening the spectrum of agricultural goods or extending the time frame might provide more profound understanding of long-term agricultural dynamics. Furthermore, it is crucial to prioritize the improvement of accessibility and usage of these forecasting tools for stakeholders at different stages of the agricultural value chain.

To summarize, the use of ARIMA and BSTS models in this work signifies a noteworthy progress in agricultural prediction for potato cultivation in Iraq. This study helps to the greater objective of promoting sustainable agriculture practices and guaranteeing food security in the area by using sophisticated analytics.

References

Ali, N. S., & Al-Juthery, H. W. (2015). The Combined Effect of Different Fertilizer Sources and irrigation method on potato and Water productivities under Iraqi conditions. International J Recent Sci Res, 6(8), 5569-5572.

Indexed at, Google Scholar

BuHamra, S., Smaoui, N., & Gabr, M. (2003). The Box–Jenkins analysis and neural networks: prediction and time series modelling. Applied Mathematical Modelling, 27(10), 805-815.

Indexed at, Google Scholar, Cross Ref

De Myttenaere, A., Golden, B., Le Grand, B., & Rossi, F. (2016). Mean absolute percentage error for regression models. Neurocomputing, 192, 38-48.

Indexed at, Google Scholar, Cross Ref

Hodson, T. O. (2022). Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geoscientific Model Development Discussions, 2022, 1-10.

Indexed at, Google Scholar, Cross Ref

Hossain, M. M., & Abdulla, F. (2016). Forecasting potato production in Bangladesh by ARIMA model. J Adv Stat, 1(4), 191-198.

Google Scholar

Jamuna, C. J., Patil, C., & Kumar, R. A. (2021). Forecasting the Price of Potato Using Time Series ARIMA Model. In Proceedings of International Conference on Communication and Computational Technologies: ICCCT 2021 (pp. 493-518). Singapore: Springer Singapore.

Google Scholar

Jun, S. (2019). Bayesian structural time series and regression modeling for sustainable technology management. Sustainability, 11(18), 4945.

Indexed at, Google Scholar, Cross Ref

Kathiar, S. A., Flaih, S. K., Mofaq, M., & Abdulkareem, M. (2019). The population density of potato (Solanum tuberosum) pests in two season plantation in Baghdad, Iraq.

Indexed at, Google Scholar

Khan, M. S., & Khan, U. (2020). Comparison of forecasting performance with VAR vs. ARIMA models using economic variables of Bangladesh. Asian Journal of Probability and Statistics, 10(2), 33-47.

Indexed at, Google Scholar, Cross Ref

Madlul, N. S., Arhaeem, F. I., Baker, Y. T., & Abdalkareem, N. A. (2020). POTATO SUPPLY RESPONSE TO CHANGES IN PRICE AND NON-PRICE FACTORS IN IRAQ DURING THE PERIOD (1989-2018). Plant Archives (09725210), 20(2).

Indexed at, Google Scholar

Marin J-M, Robert C. Bayesian Core: A Practical Approach to Computational Bayesian Statistics. 2007.

Indexed at, Google Scholar, Cross Ref

Scott, S. L., & Varian, H. R. (2014). Predicting the present with Bayesian structural time series. International Journal of Mathematical Modelling and Numerical Optimisation, 5(1-2), 4-23.

Indexed at, Google Scholar, Cross Ref

Shumway, R. H., Stoffer, D. S., & Stoffer, D. S. (2000). Time series analysis and its applications (Vol. 3, p. 4). New York: springer.

Indexed at, Google Scholar

Wagenmakers EJ, Farrell S. AIC model selection using Akaike weights. Psychonomic Bulletin & Review 2004;11:192–6.

Indexed at, Google Scholar, Cross Ref

Received: 03-Apr-2024 Manuscript No. JMIDS-24-15066; Editor assigned: 04-Apr-2024 Pre QC No. JMIDS-24-15066(PQ); Reviewed: 15-Apr-2024 QC No. JMIDS-24-15066; Revised: 22-Apr-2024 Manuscript No. JMIDS-24-15066(R); Published: 30-Apr-2024