Original Articles: 2022 Vol: 25 Issue: 5
A stochastic diffusion logistic growth price model with external jump process
Raed A Al-Husain, Kuwait University
Basel M Al-Eideh, Kuwait University
Citation Information: Al-Husain, R.A., & Al-Eideh, B.M. (2022). A stochastic diffusion logistic growth price model with external jump process. Journal of Management Information and Decision Sciences, 25(5), 1-10
Abstract
This study provides a methodology for analyzing price behavior. In place of typical before-and-after regression approaches and time series analysis, a new stochastic diffusion logistic growth price model based on stochastic differential equations is developed that explicitly accounts for price fluctuations and volatility. More specifically, we propose a stochastic version of the logistic growth price model driven by birth and death diffusion processes and random external jumps. Numerical examples for no jumps and the occurrence of jump processes that follow uniform and exponential distributions are considered. This study shows the difference between uniform jumps and exponential jumps, which indicates if the jump processes are affected by growth rates or not, and finally, shows how these differences affect stochastic diffusion logistic growth pricing models. The research indicates that modeling incorporating diffusion processes and random jumps can more accurately depict the volatility of real-life situations. Overall, the findings seem reasonable and are suggested for modeling purposes.
Keywords
Logistic Growth Model, Birth-Death Diffusion Process, External Jump Process, Stochastic Differential Equations.
Introduction
The logistic growth equation is a classic model for estimating the growth of a population with a finite carrying capacity, but when stochastic fluctuations are added, it becomes even more representative of real-world applications. Furthermore, the stochastic differential processes combine the influence of uncertainties, randomness, and risk factors in various economic units such as labor force, stock prices, and technology variables. With such a broad range of applicability, there has been increasing effort in the past decade to describe evidence of interactions with stochastic differential equation processes in dynamic economics. Accordingly, a new stochastic logistic growth process approach is used in this study to demonstrate how decision makers' concerns about model specifications can affect prices and quantities in dynamic economies. We suggest using this stochastic logistic growth model in price models because it is of a continuous-time type, which differs from the discrete-type models that are already widely used, and because this type of model has not been widely utilized in economic analyses.
Various studies have been conducted on the stochastic logistic growth model in the literature. The following are some of the most recent ones. For instance, Campillo et al. (2013) examined the stochastic logistic growth model and the Fokker-Planck equation describing the law of the process. They used its solution to build a likelihood function for the unknown parameters. Shang (2013) developed a variant of the stochastic logistic model allowing for individual variation and time-varying infection and recovery rates, which he proved can be approximated by a deterministic process defined by an integral equation as the population gets larger. Kink (2018) analyzed the stochastic logistic growth model and derived several new results. Using a closed-form, Kink computed the distribution of the solution, mean passage times, and distribution of hitting times for the martingale case. Ayoubi (2019) investigated the stability of stochastic logistic equations with Ornstein-Uhlenbeck processes and showed that the model has a positive solution and introduced the conditions for stochastically stable models. Furthermore, Prajneshu & Goshh (2019) argue that stochastic growth models can be more relevant for modeling nonlinear growth scenarios, particularly agricultural applications. Yoshioka et al. (2019) incorporated stochastic generalization into a deterministic logistic growth model to efficiently describe individual organisms' biological growth in natural environments. Tesfay et al. (2021) formulated a stochastic logistic fish growth model driven by white and non-Gaussian noise. They focused on the average time to extinction, escape probability for measuring noise-induced extinction probability, and the Fokker-Planck equation for fish population growth.
The stochastic logistic growth model has also found its way into various healthcare and public health applications. To name a few, Jiang et al. (2017) developed a stochastic HIV-I infection model with logistic growth and showed sufficient conditions for both an ergodic stationary distribution and the extinction of the infection. Liu et al. (2020) studied the stochastic Systemic Inflammatory Response Syndrome (SIRSI) epidemic model with logistic growth and general nonlinear incidence rate and established sufficient conditions for the existence of a unique ergodic stationary distribution. Another stochastic SIRS model with logistic growth and nonlinear incidence rates is examined by Rajasekar et al. (2020) and showed that the proposed stochastic SIRS model yields a global and positive result. Following Rajasekar’s model, Han et al. (2021) examined another stochastic SIRSI epidemic model with saturation incidence rate and logistic growth, and the unique solution was found to be globally positive.
Furthermore, stochastic processes have been applied to three categories of economic phenomena using stochastic differential equations: The description of growth under uncertainty, the nature of option price variations, and stochastic dynamic programming. Researchers have studied various economic components from a variety of perspectives. Aase & Guttrop (1987), for example, investigated the influence of relative security prices in the capital market using stochastic process models that may have continuous components and discrete jumps at random time points and showed how to estimate the random processes from historical prices. In addition, two other classical applications are Black and Scholes (1973) & Merton (1975), both of whom focus on processes with continuous sample paths. Harrison & Pliska (1981) and Aase (1984) are new references that also allow for jumps in the paths. Also known as "semi-martingales," this process type is characterized by continuous sample routes from the right and containing left-hand limit values (Kabanov et al., 1979).
Moreover, Al-Eideh & Hasan (2002b) considered growth price models using a solution of stochastic differential equation of the logistic price model under a random environment as well as the logistic price models with an arbitrary external jump process. They derived the time-dependent probability functions and the steady-state probability. In addition, the mean and variance, as well as the sample path of such a process, are also taken into consideration. Also, Al-Eideh (2017) presented a stochastic differential equation solution for a growth price model. Following a birth-and-death diffusion process with random external jumps, the growth price process is determined by a geometric progression of the growth rate. Finally, Zainal & Al-Eideh (2020) developed a model for the Ito diffusion price that explicitly accounts for price variations under a random environment using the general disaster process.
The stochastic process techniques are thus suitable for quantitative economics studies and allow us to obtain reliable estimates of specific economic parameters. They also offer us valuable tools for estimating parameters associated with high levels of non-sampling error.
Thus, we recommend introducing stochastic process techniques to study economic structure. This article has contributed significantly to formulating a stochastic logistic growth model, its analysis, and its application. This paper presents a new stochastic diffusion logistic growth price model based on a solution to the stochastic differential equation. In particular, we study the growth rate of the logistic growth process with a birth and death diffusion process. We also obtain a simulated sample path of such a logistic growth price process. Jump processes that follow a uniform or exponential distribution, as well as no-jump processes, are examined numerically in this paper.
A Stochstic Diffusion Logistic Growth Price Model With External Jump Process
In many cases, the growth and the decline in real prices can be well approximated by the solutions of differential equations. However, there are circumstances in which the fundamentally random nature of the price growth should be taken into account. This leads us to consider stochastic price models.
Various prices often exhibit sudden large upward or downward swings, and such external jumps, whether due to shocks, wars, pandemics like Covid-19, etc., are best interpreted as a random phenomenon.
Consider a logistic price model S(t) , assuming S(t) to be a continuous variable. then we define the stochastic diffusion logistic growth price process {S(t); t≥ 0}which is modeled by
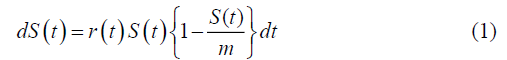
Where m is the maximum price that we expect to reach and r (t) represents the birth and death diffusion growth rate with an external jump process.
Following the same line as in Al-Eideh and Hasan [5], then the solution of the differential equation in 1 is given by equation 2
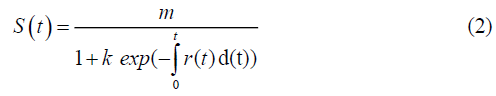
Where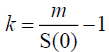 
and S(0) is the initial price at time zero.
Consider the birth and death with a jump growth rate process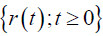 
at time t, the diffusion coefficient α and the drift coefficient b are both proportional to r (t) . It is assumed that the diffusion process is interrupted by external jumps that occur at a constant rate c with magnitudes having a distribution 
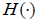. Then 
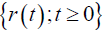is a Markov process with State-Space S = (0,∞) and can be regarded as a solution to the stochastic differential equation 3.
Here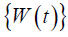 
is a Wiener process with mean zero and variance 
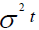.Also, 
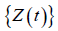is a compound Poisson process (equation 4)
Here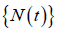 
is a Poisson process with mean rate c, where c is the external jump rate, and Y1, Y2,…, are independent and identically distributed random variables with distribution function 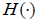, with mean 
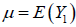and variance 
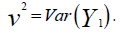Note that the moments of
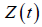can be determined from the random sums formulas, and are (equations 5 & 6)
and
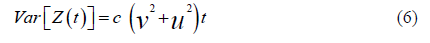
Now from equation 3, we get,
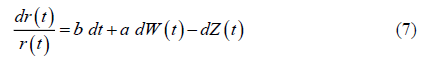
As a result, the solution to the stochastic differential equation in 7 is (equation 8)
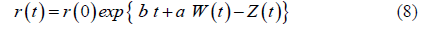
Where r (0) is the initial growth rate at time zero. Also, using Karlin & Taylor (1981) and Al-Eideh & Al-Hussainan (2002a) and after some algebraic manipulations, it can be shown that (equation 9)
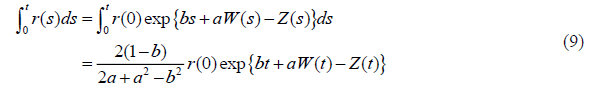
Now, rewriting equation 2, we get
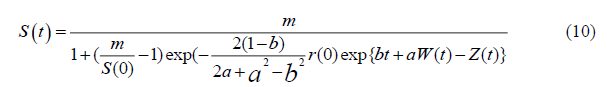
Where S (0) and r (0) are the initial price data and the initial growth rate at time zero.
The Simulated Logistic Growth Price Model S(t)
In this section, Using the birth and death diffusion growth rate process r (t) and the external jump process specified in equation 10, we will derive the simulated sample path of the logistic growth price process S (t) .
For simulation of the logistic growth price process S (t) , the following discrete approximation is used. For integer values k =1,2,3,... , and n =1,2,3,... the birth and death growth rate diffusion process r (t) with external jump process can be simulated by
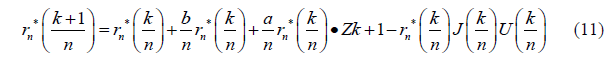
Where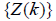 
is a sequence of independent standard normal random variables and
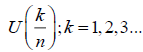are independent and identically distributed with
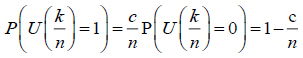
and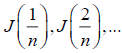 
are independent and identically distributed with distribution 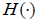. Also, note that 
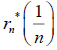is the initial growth rate at time zero.
For each set of positive integers k,t1 ,....the random vectors’ sequence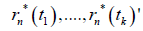 
converges to 
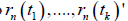in distribution.
Thus, the simulated logistic growth price model S (t) is given by (equation 12)
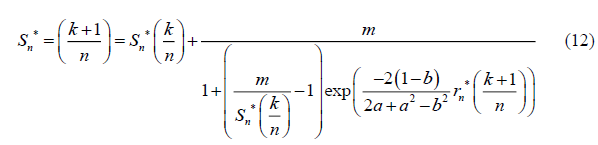
Where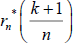 
is defined in equation 11.
Note that for each set of positive integers k, the sequence of random vectors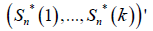 
converges in distribution to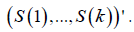 
Numerical Example
Consider as an example the following sample paths of the above logistic growth price model S (t) in section 3 that represents the annual price of an item in an anonymous country in U.S. dollars when S (0)= 0, r(0)= 0.02, m = 70, b = 0.02, a = 0 , n = 20 , and c =1 for the following cases:
Case 1
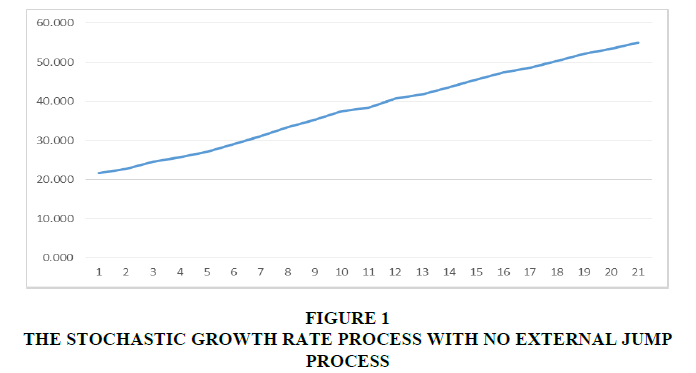
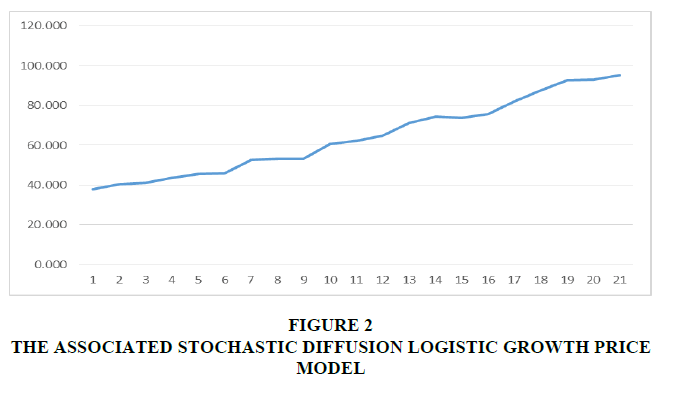
In this case, we consider the sample path to the stochastic diffusion logistic growth price model S (t) with a stochastic birth and death diffusion rate of growth r (t) and no external jump processes; note the external jump rate c = 0 . Figure 1 and Figure 2 represent this case for r (t) and S (t) respectively.
Figure 1: The Stochastic Growth Rate Process With No External Jump Process.
Figure 2: The Associated Stochastic Diffusion Logistic Growth Price Model.
Case 2
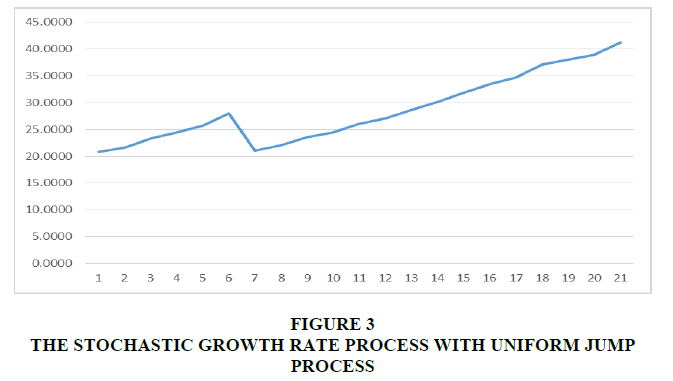
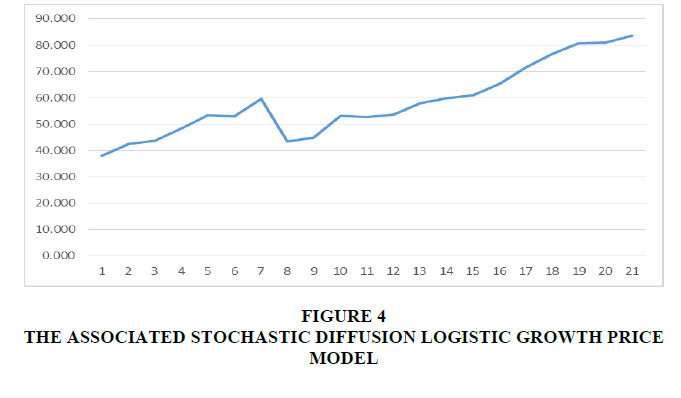
In this case, we consider the sample path to the stochastic diffusion logistic growth price model S (t) using the Stochastic birth and death diffusion growth rate process r (t) with a uniform external jump process; note the jump rate c =1in this instance. For simplicity, we take 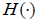to be uniform on [0,1]. Thus (equation 13),
Note that H(y) is independent of y with mean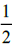 
, and variance 
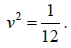Figure 3 and Figure 4 represent this case for r (t) and S (t) respectively.
Figure 3: The Stochastic Growth Rate Process With Uniform Jump Process.
Figure 4: The Associated Stochastic Diffusion Logistic Growth Price Model.
Case 3
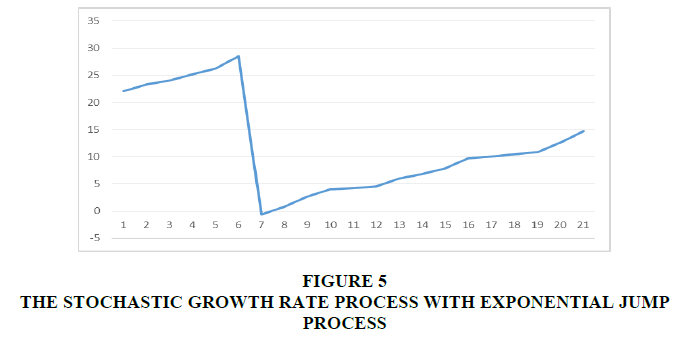
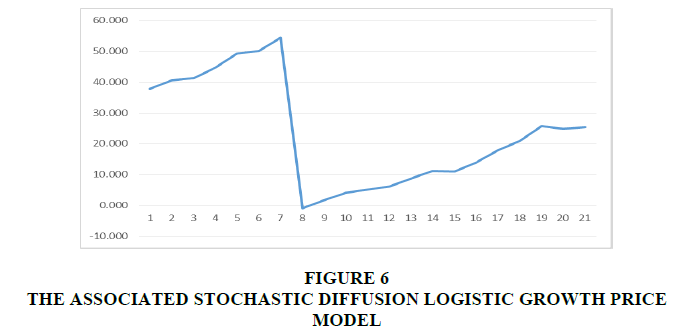
In this case, we consider the sample path to the stochastic diffusion logistic growth price model S (t) using the stochastic birth and death diffusion growth rate process r (t) with an exponential external jump process; note the jump rate c =1 in this instance. For simplicity, we take 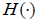to be exponential with a mean of 1. Thus,
Note that H (y) depends on y with mean 1, and variance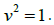 
. Figure 5 and Figure 6 represent this case for r (t) and S (t) respectively.
The above figures illustrate the difference between the uniform jump and exponential jump, which indicates whether the jump processes are dependent on or independent of growth rates and how this difference affects stochastic diffusion logistic growth pricing models. In general, the figures appear reasonable and are suggested for modeling purposes.
Figure 5: The Stochastic Growth Rate Process With Exponential Jump Process.
Figure 6: The Associated Stochastic Diffusion Logistic Growth Price Model.
Conclusion
This study offers a methodology for analyzing price behavior. It departs from traditional before and after regression approaches as well as time series analysis to develop a stochastic model which explicitly accounts for the variations and volatility of prices following a stochastic diffusion logistic growth model using a birth and death diffusion growth rate process subject to randomly occurring external jump processes, especially the uniform on [0,1] and exponential with a mean of 1 processes. The findings suggest that modeling using diffusion processes and random jumps is a more effective way to portray the volatility of real-life situations. Future research should focus on a large class of external jump processes with a general jump rate. Furthermore, this approach might be used for some inference problems. The method could be applied to a wide range of economics and operations research problems in future research, not just in pricing.
References
Aase, K. K., & Guttorp, P. (1987). Estimation in models for security prices.Scandinavian Actuarial Journal,1987(3-4), 211-224.
Indexed at, Google Scholar, Crossref
Aase, K. K. (1984). Optimum portfolio diversification in a general continuous-time model.Stochastic processes and their applications,18(1), 81-98.
Indexed at, Google Scholar, Crossref
Al-Eideh, B. M. (2017). A Stochastic Growth Price Model Using a Birth and Death Diffusion Growth Rate Process with External Jump Process.Asia Pacific Journal of Advanced Business and Social Studies (APJABSS),3(1), 345-356.
Al-Eideh, B. M., & Al-Hussainan, A. A. (2002). A quasi-stochastic diffusion process of the Lorenz curve.The International Mathematical Journal,1, 377-383.
Al-Eideh, B. M., & Hasan, M. H. (2002). Growth price model under random environment: A stochastic analysis. InTheory of Stoch. Proc(Vol. 8, No. 24, pp. 1-2).
Ayoubi, T. (2019). Stability of stochastic logistic model with Ornstein-Uhlenbeck process for cell growth of microorganism in fermentation process.Applied Mathematics,10(8), 659-675.
Indexed at, Google Scholar, Crossref
Black, F., & Scholes, M.S. (1973). The Pricing of Options and Corporate Liabilities.Journal of Political Economy, 81, 637-654.
Campillo, F., Joannides, M., & Larramendy-Valverde, I. (2013). Estimation of the parameters of a stochastic logistic growth model.arXiv preprint arXiv:1307.2217.
Han, B., Jiang, D., Zhou, B., Hayat, T., & Alsaedi, A. (2021). Stationary distribution and probability density function of a stochastic SIRSI epidemic model with saturation incidence rate and logistic growth.Chaos, Solitons & Fractals,142, 110519.
Indexed at, Google Scholar, Crossref
Harrison, J. M., & Pliska, S. R. (1981). Martingales and stochastic integrals in the theory of continuous trading.Stochastic processes and their applications,11(3), 215-260.
Indexed at, Google Scholar, Crossref
Jiang, D., Liu, Q., Shi, N., Hayat, T., Alsaedi, A., & Xia, P. (2017). Dynamics of a stochastic HIV-1 infection model with logistic growth.Physica A: Statistical Mechanics and its Applications,469, 706-717.
Indexed at, Google Scholar, Crossref
Kabanov, J.M., Lipcer, R.?., & Sirjaev, A.N. (1979). Absolute continuity and singularity of locally absolutely continuous probability distributions. I.Mathematics of The Ussr-sbornik, 35, 631-680.
Indexed at, Google Scholar, Crossref
Karlin, S., & Taylor, H. E. (1981).A second course in stochastic processes. Elsevier.
Kink, P. (2018). Some analysis of a stochastic logistic growth model.Stochastic Analysis and Applications,36(2), 240-256.
Indexed at, Google Scholar, Crossref
Liu, Q., Jiang, D., Hayat, T., Alsaedi, A., & Ahmad, B. (2020). A stochastic SIRS epidemic model with logistic growth and general nonlinear incidence rate.Physica A: Statistical Mechanics and Its Applications,551, 124152.
Indexed at, Google Scholar, Crossref
Merton, R. C. (1975). Optimum consumption and portfolio rules in a continuous-time model. InStochastic optimization models in finance(pp. 621-661). Academic Press.
Indexed at, Google Scholar, Crossref
Prajneshu, & Ghosh, H. (2019). Stochastic differential equation models and their applications to agriculture: an overview. Statistics and Applications, 17(1), 73-83.
Rajasekar, S. P., Pitchaimani, M., & Zhu, Q. (2020). Progressive dynamics of a stochastic epidemic model with logistic growth and saturated treatment.Physica A: Statistical Mechanics and Its Applications,538, 122649.
Indexed at, Google Scholar, Crossref
Shang, Y. (2013). The limit behavior of a stochastic logistic model with individual time-dependent rates.Journal of Mathematics,2013, 502635.
Indexed at, Google Scholar, Crossref
Tesfay, A., Tesfay, D., Khalaf, A., & Brannan, J. (2021). Mean exit time and escape probability for the stochastic logistic growth model with multiplicative a-stable L