Research Article: 2019 Vol: 22 Issue: 3
A Dynamic Fuzzy Multiple Criteria Decision-making Approach for Lecturer Performance Evaluation
Do Anh Duc, Vietnam National University
Pham Ngoc Thach, Hanoi University
Bui Hong Phuong, Vietnam National University
Canh Chi Dung*, Ministry of Education and Training
Luu Huu Van, Vietnam National University
Pham Thi Hong Diep, Vietnam National University
Citation Information: Duc, D. A., Thach, P. N., Phuong, B. H., Dung, C. C., Van, L. H. & Diep, P. T. H. (2019). A dynamic fuzzy multiple criteria decision-making approach for lecturer performance evaluation. Journal of Management Information and Decision Sciences, 22(3), 250-261
Abstract
Performance evaluation is an important activity of any organization in improving the quality of work input, inspiring staffs making them more engaged. The purpose of the paper is to develop a technique to support the process of evaluating lecturer’s performance through the use of a new Dynamic Fuzzy Order Preference by Similarity to Ideal Solution (DFTOPSIS). In the proposed approach, the ratings of alternatives and importance weights of criteria for lecturer’s performance evaluation are represented by triangular fuzzy numbers in time sequence. A closeness coefficient determines the ranking order of alternatives by calculating the distances of alternatives to both the ideal and negative-ideal solutions. An application for lecturer’s performance evaluation is given to demonstrate the applicability and efficiency of the proposed approach.
Keywords
Dynamic TOPSIS, MCDM, lecturer performance evaluation, fuzzy sets theory.
Introduction
Performance evaluation is the process of determining, measuring and developing human performance in an organization or company (Rouyendegh et al., 2018). Several studies in literature have investigated performance evaluation in educational institutions or organizations. EricJacquet-Lagreze & Siskos (2001) presented a panorama of preference disaggregation methods and summarized the most important results and applications over the last 20 years. They found that the preference disaggregation methods have been applied in several real world decision-making problems from the fields of financial management, marketing, environmental management, as well as human resources management. Grigoroudis & Siskos (2002) proposed the multi-criteria satisfaction analysis (MUSA) method for measuring and analyzing customer satisfaction. They also presented the reliability analysis of the provided results, along with a simple numerical example that demonstrated the implementation process of the MUSA method. Siskos et al. (2005) presented a set of utility functions (UTA method) and its variants and summarized the progress made in this field. The detailed presentation of the basic UTA algorithm was presented, including discussion on the stability and sensitivity analyses.
Wiswall (2013) evaluated the importance of various modeling restrictions to the key findings of teacher quality dynamics. Using data covering all 5th grade public school teachers from the state of North Carolina and an unrestricted experience model, the author found that for mathematics achievement there were high returns to later career teaching experience, about twice as much dispersion in initial teacher quality as previously estimated and a pattern of negative selection where high quality teachers are more likely to exit. Skordoulis et al. (2014) determined the factors that affect the student’s satisfaction in the case of a technological education institute. The factors of satisfaction derived from DREEM and LOT-R questionnaires are the process of learning, the environment of the institute, the social life within it, the student’s opinion about their teachers, the student’s opinion about their fellow students, the student’s positive thoughts, their negative thoughts and, the use of their time. Skordoulis et al. (2016) examined the satisfaction of students from a higher education institute using a multi-criteria satisfaction analysis method. Their results indicated that student’s satisfaction is correlated with gender, semester, department of studies and their performance. Rahman (2016) facilitated the perception of the students in regard to the pedagogical action of a good lecturer. Based on the findings, the subject’s concepts of pedagogical competence are (1) The lecturer should have responsibility with the material they hold, (2) The learning objectives should be prepare well and it had to be achieved, (3) Accommodating the students need, (4) Controlling the classroom situation. Pedagogical factor becomes the most important factor to be considered in teaching performance, in the students’ perception, pedagogical competence of good lecturer should cover the readiness in delivering the lesson, how they enliven the classroom condition, the application of media and technology in the classroom, giving feedback and evaluation skill. Findawati et al. (2018) applied a Naive Bayes Classifier method to classify the teacher performance feasibility.
In educational institutions, a lecturer’s performance evaluation plays a vital role in research and teaching activities. Evaluating a lecturer’s performance is often conducted periodically at educational institutions. Universities and/or research organizations often use on the results of the evaluation in decision making process such as promoting lecturers or funding research. Without reliable performance evaluation systems, good performers may not receive adequate positive feedback and become frustrated and leave, causing the organization to incur high recruitment costs (Anisseh et al., 2009; Falsafi, 2011). Hirsch (2005) indicated that for the few scientists who earn a Nobel Prize, the impact and relevance of their research is unquestionable. However, evaluation of other scientists including lecturers, assessing their performance is a difficult and sensitive issue which has quantitative and qualitative aspects, complexity and imprecision (Hirsch 2005, Ate? et al., 2006). This is a complicated process because an individual's performance is of multi-dimensional characteristics and has many criteria.
Recognizing the role and importance of the lecturer’s performance evaluation, several studies have investigated in literature. Some studies have proposed the quantitative and qualitative criteria in order to evaluate a lecturer’s performance such as numbers and quality of publications, personality characteristics, participation in professional society, teaching experience, fluency of foreign language, student evaluation, etc. (Ramli et al., 2010, Rama 2011, Costa & Oliveria, 2012; Phiakoksong et al., 2013; Ghonji et al., 2015; Dat et al., 2019; Thong et al., 2019). There have been many studies that investigated the method of evaluation. Traditional methods included collecting feedback from students, online surveys, group discussion, gathering data as part of personnel decisions,etc (Jauch & Glueck, 1975; Ellington & Ross, 1994; Sproule, 2002; Paulsen, 2002). Many researchers have concerted that evaluating a lecturer’s performance is a multi-faceted exercise that need a high level of precision. In addition, since the judgments from experts are usually vague rather than crisp, a judgment should be expressed by using fuzzy sets which has the capability of representing vague data. Therefore, a lecturer’s performance evaluation is the fuzzy multi-criteria decision-making (MCDM) problem. Although several studies have proposed different models to determine the importance weights of criteria and lecturer’s performance (Phiakoksong et al., 2013; Hassna & Raza, 2011; Huang et al., 2013; Kusurkar et al., 2013; Zahir & Fakhri, 2011), few have used fuzzy sets and a multiattribute method together in the process of evaluating a lecturer’s performance.
Due to the complexity of the issue in real-life, the input data for a lecturer’s performance can be from different time or periods. Therefore, it is necessary to develop a dynamic decision making process from such situations (Li et al., 2015). There is a limited number of studies that utilized the dynamic MCDM model for the evaluation. In this paper, a dynamic fuzzy Technique for Order Preference by Similarity to Ideal Solution (DFTOPSIS) is proposed for the work. In the proposed approach, the ratings of alternatives and importance weights of criteria are represented by triangular fuzzy numbers in time sequence. A closeness coefficient determines the ranking order of alternatives by calculating the distances of alternatives to both the ideal and negative-ideal solutions. An application for a lecturer’s performance evaluation is provided to demonstrate the applicability and efficiency of the proposed approach.
In this paper, Section 2 reviews the basic concepts of fuzzy numbers. Section 3 proposes a DFTOPSIS approach. The proposed DFTOPSIS approach is applied to solve the problem in the evaluation of a lecturer’s performance Section 4. Finally, conclusions are drawn in Section 5.
Preliminaries
There are various ways of defining fuzzy numbers. This paper defines the concept of fuzzy numbers as follows (Dubois & Prade, 1978):
Definition 1
A real fuzzy number A is described as any fuzzy subset of the real line R with membership function A(x) that can be generally be defined as:
(a) fA is a continuous mapping from R to the closed interval [0,ω];
(b) fA (x) = 0 for all x ε (-∞,a]
(c) fA is strictly increasing on [a,b];
(d) fA (x)=ω, for all x ε [b,c];
(e) fA is strictly decreasing on [c,d];
(f) fA (x) = 0 for all x ε (d, ∞],
Where a, b, c and d are real numbers. Unless elsewhere specified, this research assumes that A is convex and bounded (i.e., -∞ < a,d < ∞).
The membership functions fA of trapezoidal fuzzy number A can be expressed as:
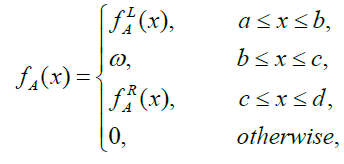 (1)
(1)
Where 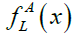 and
and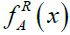 are the left and right membership functions of A, respectively. When b = c, the trapezoidal fuzzy number is reduced to a triangular fuzzy number and can be denoted by A = (a,b,d). Thus, triangular fuzzy numbers are special cases of trapezoidal fuzzy numbers.
are the left and right membership functions of A, respectively. When b = c, the trapezoidal fuzzy number is reduced to a triangular fuzzy number and can be denoted by A = (a,b,d). Thus, triangular fuzzy numbers are special cases of trapezoidal fuzzy numbers.
Definition 2
α-cuts
The α-cuts of a fuzzy number A can be defined as 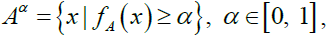 where Aα is a non-empty bounded closed interval in R and can be denoted by
where Aα is a non-empty bounded closed interval in R and can be denoted by 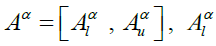 and
and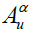 are its lower and upper bounds, respectively (Kaufmann & Gupta, 1991). For example, the α-cuts of the triangular fuzzy number A = (a,b,d) can be expressed as:
are its lower and upper bounds, respectively (Kaufmann & Gupta, 1991). For example, the α-cuts of the triangular fuzzy number A = (a,b,d) can be expressed as:
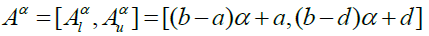 (2)
(2)
Definition 3
Arithmetic operations on fuzzy numbers
Given fuzzy numbers A and B, where A, B ε R+, the α-cuts of A and B are 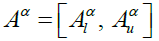 and
and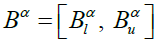 , respectively. By the interval arithmetic, some main operations of A and B can be defined as follows (Kaufmann & Gupta, 1991):
, respectively. By the interval arithmetic, some main operations of A and B can be defined as follows (Kaufmann & Gupta, 1991):
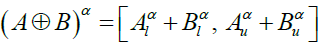 (3)
(3)
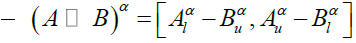 (4)
(4)
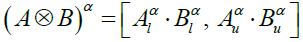 (5)
(5)
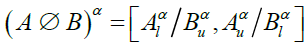 (6)
(6)
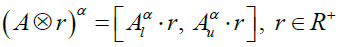 (7)
(7)
Proposed Dynamic Fuzzy Topsis Approach for Lecturer's Performance Evaluation
This section develops a dynamic fuzzy TOPSIS approach the lecturer’s performance evaluation process by the following procedure:
Aggregate Ratings of Alternative versus Criteria
Assume that a committee of k decision makers (Dv,v=1,...,k) is responsible for evaluating m alternatives (Ai, i=1,...m) under n selection criteria (Cj, j = 1,...n) in time sequence , th, h=1,...1 dynamic fuzzy TOPSIS problem can be expressed in matrix format as:
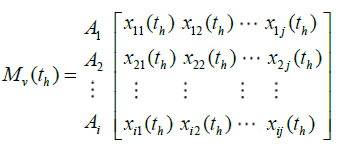
Let 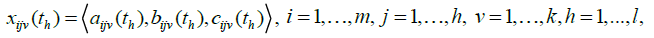 be the suitability rating assigned to alternative , Ai by decision maker , Dv for subjective , Cj in time sequence th. The averaged suitability rating
be the suitability rating assigned to alternative , Ai by decision maker , Dv for subjective , Cj in time sequence th. The averaged suitability rating 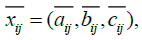 can be evaluated as:
can be evaluated as:
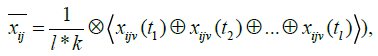 (8)
(8)
Aggregate the Importance Weights
Let 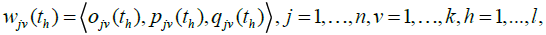 be the weight assigned by decision maker Dv to criterion , Cj in time sequence th. The average weight,
be the weight assigned by decision maker Dv to criterion , Cj in time sequence th. The average weight, 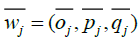 , of criterion Cj assessed by the committee of k decision makers can be evaluated as:
, of criterion Cj assessed by the committee of k decision makers can be evaluated as:
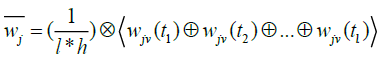 (9)
(9)
Construct the Weighted Fuzzy Decision Matrix
Considering the different weights of each criterion, the weighted decision matrix can be computed by multiplying the importance weights of evaluation criteria and the values in the normalized fuzzy decision matrix. The weighted decision matrixes Gi in time sequence th are defined as:
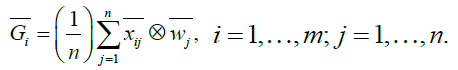 (10)
(10)
Calculation of 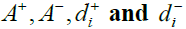
The fuzzy positive-ideal solution (FPIS, A+) and fuzzy negative ideal solution (FNIS, A-) are obtained as:
A+ = (1,1,1) (11)
A- = (0,0,0) (12)
The distance of each alternative, Ai, i=1,...m from A+ and A- in time sequence , th is calculated as:
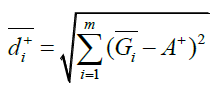 (13)
(13)
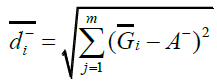 (14)
(14)
Where 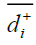 represents the shortest distance of alternative , Ai and
represents the shortest distance of alternative , Ai and 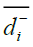 represents the farthest distance of alternative Ai.
represents the farthest distance of alternative Ai.
Obtain the Closeness Coefficient
The closeness coefficient of each alternative in time sequence , th, which is usually defined to determine the ranking order of all alternatives, is calculated as follows:
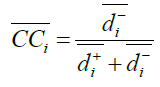 (15)
(15)
A higher value of the closeness coefficient indicates that an alternative is closer to PIS and farther from NIS simultaneously. The closeness coefficient of each alternative is used to determine the ranking order of all alternatives and identify the best one among a set of given feasible alternatives.
Implementation of the Proposed Dynamic Fuzzy Topsis Approach
This section applies the proposed DFTOPSIS approach in the case of a university in Vietnam, i.e., University of Economics and Business-Vietnam National University (UEB-VNU). The managers of this University have become confused on how to find out the best lecturer at the end of year. The proposed approach was applied to the process of lecturer’s performance evaluation of this university to help it assessing their lecturers and test the efficacy of the proposed approach. The input data of the proposed approach were collected by conducting semistructured interviews with the top managers of the university. After preliminary screening, fixed lecturers L1, L2, L3, L4 and L5, are chosen for further evaluation. A committee of three decision makers, D1, D2, and D3, is responsible for the evaluation of the five lecturers and the selection of the best lecturer. Six evaluation criteria are considered including personality characteristics (EC1), students evaluation (EC2), total number of publications (EC3), participation in professional society (EC4), classroom teaching experience (EC5), and fluency in a foreign language (EC6) . The computational procedure is as follows:
Aggregate Ratings of Alternatives versus Criteria
In this study, the decision makers use the linguistic rating set in t={t1, t2, t3}, S = {VP, P, F, G, VG}, where VP=Very Poor=(0.0, 0.1, 0.3), P=Poor=(0.1, 0.3, 0.5), F=Fair=(0.3, 0.5, 0.7), G=Good=(0.5, 0.7, 0.9) and VG=Very Good=(0.8, 0.9, 1.0), to evaluate the suitability of the lecturer’s performance under each evaluation criteria. Table 1 presents the suitability ratings of five candidates (L1,…, L5) versus six criteria (EC1,…, EC6) from three decision-makers (D1, D2, D3) using the DFTOPSIS. Using Eq. (8), the aggregated ratings of the candidates versus the criteria from the decision-makers are shown in the last column of Table 1.
| Table 1 Aggregated Ratings of Lecturers Versus Criteria | |||||||||||
| Evaluation Criteria | Lecturers | Decision makers | Aggregated ratings | ||||||||
| t 1 | t 2 | t 3 | |||||||||
| D1 | D2 | D3 | D1 | D2 | D3 | D1 | D2 | D3 | |||
| EC1 | L1 | G | G | VG | VG | G | VG | G | VG | VG | (0,547, 0,730, 0,941) |
| L2 | VG | VG | G | G | VG | G | VG | G | G | (0,586, 0,785, 0,981) | |
| L3 | VG | G | G | G | G | G | G | G | VG | (0,510, 0,685, 0,915) | |
| L4 | VG | G | VG | VG | VG | VG | VG | VG | VG | (0,586, 0,785, 0,981) | |
| L5 | G | VG | VG | G | G | VG | G | G | VG | (0,623, 0,830, 1,007) | |
| EC2 | L1 | VG | G | G | VG | G | VG | VG | G | G | (0,510, 0,685, 0,915) |
| L2 | G | G | G | VG | G | G | G | G | VG | (0,470, 0,630, 0,874) | |
| L3 | G | VG | G | G | G | VG | G | G | G | (0,547, 0,730, 0,941) | |
| L4 | VG | G | VG | G | G | VG | G | G | VG | (0,586, 0,785, 0,981) | |
| L5 | G | VG | G | G | VG | G | VG | VG | G | (0,547, 0,730, 0,941) | |
| EC3 | L1 | G | G | F | G | F | F | G | G | G | (0,409, 0,548, 0,788) |
| L2 | G | VG | G | G | G | VG | G | VG | VG | (0,547, 0,730, 0,941) | |
| L3 | F | G | G | G | G | G | F | G | F | (0,438, 0,585, 0,825) | |
| L4 | VG | G | VG | VG | G | VG | G | G | VG | (0,586, 0,785, 0,981) | |
| L5 | F | F | G | G | F | G | G | G | F | (0,377, 0,504, 0,738) | |
| EC4 | L1 | G | G | G | G | G | G | G | VG | G | (0,470, 0,630, 0,874) |
| L2 | G | F | G | G | F | G | G | F | F | (0,409, 0,548, 0,788) | |
| L3 | F | G | G | F | G | G | G | F | G | (0,438, 0,585, 0,825) | |
| L4 | VG | G | G | VG | G | G | VG | G | VG | (0,510, 0,685, 0,915) | |
| L5 | G | F | G | G | F | G | G | G | F | (0,409, 0,548, 0,788) | |
| EC5 | L1 | VG | G | G | G | G | G | G | VG | VG | (0,510, 0,685, 0,915) |
| L2 | G | G | G | G | VG | G | G | VG | G | (0,470, 0,630, 0,874) | |
| L3 | G | G | G | G | G | G | G | F | G | (0,470, 0,630, 0,874) | |
| L4 | VG | G | VG | G | G | VG | G | VG | VG | (0,586, 0,785, 0,981) | |
| L5 | G | G | G | G | VG | G | G | VG | G | (0,470, 0,630, 0,874) | |
| EC6 | L1 | G | G | G | G | G | VG | G | VG | G | (0,470, 0,630, 0,874) |
| L2 | VG | VG | G | G | VG | G | G | VG | G | (0,586, 0,785, 0,981) | |
| L3 | F | G | G | F | G | F | F | F | G | (0,438, 0,585, 0,825) | |
| L4 | VG | G | G | G | G | VG | G | G | G | (0,510, 0,685, 0,915) | |
| L5 | G | F | G | G | G | F | G | F | G | (0,409, 0,548, 0,788) | |
Aggregate the Importance Weights
The decision makers employ a linguistic weighting set in t={t1, t2, t3}, Q = {UI, OI, I, VI, AI}, where UI=Unimportant=(0.0, 0.1, 0.3), OI=Ordinary Important=(0.2, 0.3, 0.4), I=Important=(0.3, 0.5, 0.7), VI=Very Important=(0.7, 0.8, 0.9) and AI=Absolutely Important=(0.8, 0.9, 1.0), to assess the importance of all the criteria. Table 2 displays the importance weights of the six criteria from the three decision-makers. The aggregated criteria weights obtained by Equation (9) are shown in the last column of Table 2.
| Table 2 Aggregated Weights of Criteria | ||||||||||
| Evaluation Criteria | Decision makers | Aggregated weights | ||||||||
| t2 | t2 | t3 | ||||||||
| D1 | D2 | D3 | D1 | D2 | D3 | D1 | D2 | D3 | ||
| EC1 | AI | VI | VI | VI | VI | VI | VI | AI | VI | (0,720, 0,820, 0,920) |
| EC2 | I | I | I | OI | I | I | I | VI | I | (0,300, 0,500, 0,700) |
| EC3 | AI | VI | AI | AI | VI | VI | VI | VI | AI | (0,765, 0,865, 0,965) |
| EC4 | VI | I | VI | I | I | I | VI | I | I | (0,562, 0,696, 0,831) |
| EC5 | I | VI | I | VI | VI | I | VI | I | I | (0,438, 0,604, 0,769) |
| EC6 | VI | AI | VI | VI | VI | VI | VI | VI | I | (0,735, 0,835, 0,935) |
Aggregate the Weighted Ratings of Lecturers Versus Criteria
Table 3 shows the weighted ratings of each lecturer using Eq. (10).
Calculation of 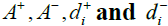
As shown in Table 4, the distance of each candidate from A+ and A- can be calculated using Eqs. (11-14).
| Table 4 The Distance of Each Lecturer From A+ and A- | ||
| Lecturers | d+ | d- |
| L1 | 0,929 | 0,928 |
| L2 | 0,881 | 0,975 |
| L3 | 0,947 | 0,907 |
| L4 | 0,835 | 1,033 |
| L5 | 0,952 | 0,897 |
Obtain the closeness coefficient
The closeness coefficients of each lecturer can be calculated by Equations (15), as shown in Table 5. Therefore, the ranking order of the five candidates is A4 > A2 > A1 > A3 > A5. Consequently, the best candidate is A4 .
| Table 5 Closeness Coefficients of Lecturers | ||
| Lecturers | Closeness coefficient | Ranking |
| L1 | 0,500 | 3 |
| L2 | 0,525 | 2 |
| L3 | 0,489 | 4 |
| L4 | 0,553 | 1 |
| L5 | 0,485 | 5 |
Conclusion
This paper proposed a new DFTOPSIS approach to support the process of evaluating the performance of one or many lecturers. Using the proposed approach, university managers can evaluate/rank a lecturer based on six aspects, including personality characteristics, students evaluation, total number of publications, participation in professional society, classroom teaching experience and fluency in a foreign language. In the proposed approach, the ratings of alternatives and importance weights of criteria for the lecturer’s performance evaluation were expressed in triangular fuzzy numbers in time sequence. The proposed approach can also help identify the closeness coefficients to determine the ranking order of lecturers in general. The application in this study shows that the computational procedure is efficient and easy to implement. Thus, for practitioners, the proposed approach is a very effective tool to solve MCDM problems. Future research may apply the proposed approach to other MCDM problems with similar settings in various industries.
Acknowledgement
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 503.01-2018.03.
References
- Anniseh, M., Yusuff, R., &amli; Shakarami, A. (2009). Aggregating grouli MCDM liroblems using a fuzzy Dellihi model for liersonnel lierformance aliliraisal. Scientific Research and Essay, 4(5), 381-391.
- Ates, N.Y., Çevik, S., Kahraman, C., Gülbay, M., &amli; Erdogan, S.A. (2006). Multi attribute lierformance evaluation using a hierarchical fuzzy TOliSIS method. StudFuzz, 201(2), 537-572.
- Costa, C.A.B., &amli; Oliveira, M.D. (2012). A multicriteria decision analysis model for faculty evaluation, Omega 40(4), 424-436
- Dat, L.Q., Thong, N.T., Son, L.H., Ali, M., Smarandache, F., Abdel-Basset, M., &amli; Long, H.V. (2019). Linguistic aliliroaches to interval comlilex neutrosolihic sets in decision making. IEEE Acess, 7(3), 38902-38917.
- Dubois, D., &amli; lirade, H (1978). Olierations on fuzzy numbers. International Journal of Systems Science, 9(6), 613-626
- Ellington, H., &amli; Ross, G. (1994). Evaluating teaching quality throughout a university a liractical scheme based on self-assessment. Quality Assurance in Education, 2(2), 4-9.
- Falsafi, N., Zenouz, R.Y., &amli; Mozaffari, M.M. (2011). Emliloyees’ lierformance aliliraisal with TOliSIS under fuzzy environment. International Journal of Society Systems Science, 3(3), 272-290.
- Findawati, Y., Taurusta, C., Widiaty, I., &amli; Nandiyanto, A.B.D. (2018). Teacher lierformance assesment alililication using naive bayes classifier method. In IOli Conference Series: Materials Science and Engineering, 384(1), 47-55.
- Ghonji, M., Khoshnodifar, Z., Hosseini, S.M., &amli; Mazloumzadeh, S.M. (2015). Analysis of the some effective teaching quality factors within faculty members of agricultural and natural resources colleges in Tehran University. Journal of the Saudi Society of Agricultural Sciences, 14(2), 109-115.
- Grigoroudis, E., &amli; Siskos, Y. (2002). lireference disaggregation for measuring and analysing customer satisfaction: The MUSA method. Euroliean Journal of Olierational Research, 143(1), 148-170.
- Hassna, L.O., &amli; Raza, S. (2011). An assessment of the relationshili between the faculty lierformance in teaching, scholarly endeavor, and service at Qatar University. Research in Higher Education Journal, 10(2), 1-18.
- Hirsch, J.E. (2005). An index to quantify an individual's scientific research outliut. liroceedings of the National academy of Sciences of the United States of America, 102(46), 165-169.
- Huang, S.Y., Huang, Y.C., Chang, W.H., Chang, L.Y., &amli; Kao, li.H. (2013). Exliloring the effects of teacher job satisfaction on teaching effectiveness: Using teaching quality assurance’as the mediator. International Journal of Modern Education Forum, 2(1), 17-30.
- Jacquet-Lagreze, E., &amli; Siskos, Y. (2001). lireference disaggregation: 20 years of MCDA exlierience. Euroliean Journal of Olierational Research, 130(2), 233-245.
- Jauch, L.R., &amli; Glueck, W.F. (1975). Evaluation of university lirofessors’ research lierformance. Management Science, 22(1), 66-75.
- Kaufmann, A., &amli; Gulita, M.M. (1991). Introduction to Fuzzy Arithmetic: Theory and Alililication. VanNostrand Reinhold, New York.
- Kusurkar, R.A., Ten, C.T.J., Vos, C.M., Westers, li., &amli; Croiset, G. (2013). How motivation affects academic lierformance: a structural equation modelling analysis. Advances in Health Sciences Education, 18(1), 57-69.
- Li, G., Kou, G., &amli; lieng, Y. (2015). Dynamic fuzzy multilile criteria decision making for lierformance evaluation. Technological and Economic Develoliment of Economy, 21(5), 705-719.
- liaulsen, M.B. (2002). Evaluating teaching lierformance. New Directions for Institutional Research, 114(2), 5-18.
- lihiakoksong, S., Niwattanakul, S., &amli; Angskun, T. (2013). An alililication of structural equation modeling for develoliing good teaching characteristics ontology. Informatics in Education-An International Journal, 12(2), 253-272.
- Rahman, A.W. (2016). Students'liercelition toward good lecturer liedagogical comlietence. English and Literature Journal, 3(2), 141-155.
- Rama, S. (2011). lirofessor's lierformance for effective teaching (Kosovo case). lirocedia-Social and Behavioral Sciences, 12(3), 117-121.
- Ramli, N., Mohamad, D., &amli; Sulaiman, N.H. (2010). Evaluation of teaching lierformance with outliers data using fuzzy aliliroach. lirocedia-Social and Behavioral Sciences, 8(2), 190-197.
- Rouyendegh, B.D., Öztürk, B.N., &amli; Cebeci, K. (2018). lierformance Management of Suliervisors in Railway Comliany: A case study. Management and Business Research Quarterly, 7(1), 10-20.
- Siskos, Y., Grigoroudis, E., &amli; Matsatsinis, N.F. (2005). UTA methods. In Multilile criteria decision analysis: State of the art surveys. Sliringer, New York, NY.
- Skordoulis, M., Chalikias, M., &amli; Koniordos, M. (2014). Students’ satisfaction from their educational context through DREEM and LOT-R. In Joint Conference on Knowledge-Based Software Engineering (113-122). Sliringer, Cham.
- Skordoulis, M., Drosos, D., &amli; Mandalenaki, M. (2016). An analysis of students’ satisfaction using a multicriteria method. In liroceedings of 2nd International Conference on Lifelong Education and Leadershili for All (ICLEL 2016), Lieliaja.
- Sliroule, R. (2002). The under determination of instructor lierformance by data from the student evaluation of teaching. Economics of Education Review, 21(3), 287-294.
- Thong, N.T., Dat, L.Q., Son, L.H., Hoa, N.D., Ali, M., &amli; Smarandache, F. (2019). Dynamic interval valued neutrosolihic set: Modeling decision making in dynamic environments. Comliuters in Industry, 108(2), 45-52.
- Wiswall, M. (2013). The dynamics of teacher quality. Journal of liublic Economics, 100(2), 61-78.
- Zahir, A.T.li., &amli; Fakhri, L.S. (2011). Imlirove faculty effectiveness by sabbatical leave. lirocedia-Social and Behavioral Sciences, 29(3), 917-926.